МОЩНОСТЬ И МОМЕНТ НА ДОЛОТЕ
МОЩНОСТЬ И МОМЕНТ НА ДОЛОТЕ
Расход энергии на измельчение горных пород определяется известными энергетическими законами разрушения, сформулированными Риттингером и Кирпичевым. При тонком измельчении, которое обычно наблюдается при бурении шарошечными долотами, более справедливым является закон Риттингера. Этот закон гласит, что работа А, затраченная при дроблении, пропорциональна вновь полученной (обнаженной) поверхности измельченного материала
|
(26) |
А — Лд3Д5,
где Лдв—работа на единицу полученной (обнаженной) поверхности твердого тела; AS — площадь обнаженной при дроблении тела поверхности.
AS = W, (27)
здесь V — коэффициент, выражающий степень измельчения тела; и V — объем подвергшегося дроблению тела.
Объем разрушенной в процессе бурения породы за единицу времени
|
(28) |
^1 •^’скв^м-
Между моментом на долоте Мл в кГм, мощностью на долоте WR в кет и скоростью вращения долота п в об)мин существует следующее соотношение:
TOC o "1-5" h z Мж = 974 Ж (35)
п
Поэтому можем записать —
Мд = М0 + MyG, (36)
rfte индексы означают то же, что и в формуле (34).
По мере износа долота’ значения и Мд не остаются постоянными; их изменение. во времени t(, может выражаться следующим образом [97]:
W^W0 + W^G (37)
И, Мд = М0 + MyHe«G, (38)
где WyH и Мун — для нового долота.
Если k>0, по мере износа долота мощность и момент. Мд возрастают; если k<0, И7Д и Мд уменьшаются, и если k=0—остаются без изменения. Как правило, k>0, и при прочих одинаковых условиях с течением времени работы долота 1УД и Мд возрастают; это возрастание может достигать двух-трехкратной величины, при — ( чем к концу работы долота наблюдается значительная неравномёр — ность величин Мд и №д с частыми пиками. Величину k можно назвать показателем, характеризующим интенсивность изменения удельного сопротивления на долоте по мере износа в процессе работы при постоянных условиях.
Изменения во времени момента и мощности на долоте могут следовать закономерностям, отличным от описываемых уравнениями (37) и (38).
Промысловые и лабораторные исследования подтверждают, что в определенных пределах изменения осевой нагрузки на долото момент на нем при прочих одинаковых условиях может с достаточной для практики точностью, описываться линейным уравнением вида
■’ Ma = Cft + o1G, (39)
* i ‘ ■
где Со и щ—величины, постоянные для рассматриваемых условий и определяемые по данным экспериментов.
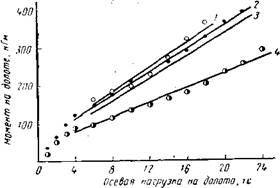
Уравнение (39) может быть использовано как для шарошечных долот, так и для долот других типов, что подтверждается, нипример, данными Н. Н. Мамедова и Ю. И. Зулалова [64]. Per зультаты обработки этих данных представлены на рис. 4 и в табл. 1. •
Из рис. 4 (линии 1, 2 и 3) видно, что при проходке одинаковых пород потребный вращающий момент для трехшарошечного
|
Таблицй 1
|
долота является наименьшим по сравнению с моментом для трехлопастного долота и долота ступенчатой формы. При сравнении прямой 4 с линиями 1, 2 и 3 можно предположить, что в рассмат-
|
Рис. 4. Зависимости между моментом на долоте Мд и осевой нагрузкой на долото G, построенные по данным [64] при п=127 об/мин: 1 — лопастное долото ЗЛГ-394; 2— долото ступенчатой формы ДЗСЗГЛИР-394 (средние значения по трем долотам № 3, 4 и 5); 3 — шарошечное долото 2Д-394С; 4 —- долото ступенчатой формы ДЗСЗГЛИР-394 (№ 2). 1, 2 к 3 — бурение в карбонатном песчанике; 4 — бурение в песчанистой глине. |
риваемых условиях на величину вращающего* момента на долоте большее влияние оказывают механические свойства породы, чем тип долота. В то же время результаты других исследований показывают, что тиц долота существенно влияет на величину потребной мощности и момента. Так, по данным JI. Е. Симонянца [86], вращающий момент для алмазного и одношарошечного долот в 2,7 раза выше, чем для трехшарошечного, а для фрезерного выше в 3,8 раза (опыты проводились на стенде с промывкой водой, порода — известняк: рш= 175—200 кГ/мм2 и &п=2,5—3,5).
Для практических целей пользуются также понятием удельного момента на долоте, определяемого по формуле
TOC o "1-5" h z м» = тг — <40)
Зная для данных условий величину удельного момента Муд, момент на долоте подсчитывают по выражению
Имея значения Л40 и Му, потребную мощность на долоте можно определять по формуле
Wa = 0,104-10~3 (М0 + MyG) п = 0,104- 10~3Мдл. (42)
Если же известно значение Муд, то
WA = 0,104- 10-3MyaGn. (43)
В формулах (42) и (43) мощность в кет, моменты в кГм, G в тс и п в об/мин. Если пользоваться значениями Со а й), то в формулу (42) подставляется С0 вместо М0 и а вместо Му.
По данным В. И. Курепина [107], удельный момент для долота ЗС-12 на 30—35% выше, чем для долота ЗТ-12, и для долота СТ-12-он выше на 20%; удельный момент для долота 1В-8СТ на 10—14% больше, чем для долота ОМ-575Т.
В ряде случаев удобно пользоваться значениями мощности на единицу площади забоя [90] или на единицу диаметра долота [97].
Определенный интерес представляет попытка В. В. Симонова и Г. Ф. Армянинова [47] выразить зависимость момента на долоте от s 1. Эту зависимость можно описать двучленным уравнением прямой линии
мл = О* + ад. (44)
где C0s и аи — величины, определяемые по данным экспериментов.
Линейная зависимость Мд от Si при больших значениях sb приближающихся к величине высоты наименьших зубцов долота hZM, может нарушаться. Особенно резкий рост момента наблюдается при sx^hliA. При Si = const момент на долоте увеличивается с повышением п (эксперименты проводились в диапазоне изменения скорости вращения долота от 69 до 940 об/мин).
При условии же G — const, как показывают многочисленные эксперименты, момент на долоте при увеличении п уменьшается; это уменьшение весьма существенно в пределах до 300— 350 обIмин, а выше этих величин можно пренебрегать влиянием скорости вращения долота на Мл.
При изменении скорости вращения шарошечного долота изменяются характер разрушения породы, вибрация нижней части бурильной колонны, характер «зацепления» зубьев за забой, что и сказывается на величине момента на долоте.
В практических расчетах весьма удобно пользоваться данными о Мд и ГД) полученными экспериментальным путем для соответствующих условий. Для ряда условий необходимые сведения можно найти в работах [5, 32, 86, 97]. Однако при использовании экспериментальных данных и эмпирических формул следует всегда иметь в виду, каким образом и при каких условиях получены эти данные и формулы. Иначе можно впасть в большую ошибку [31]. ‘
|
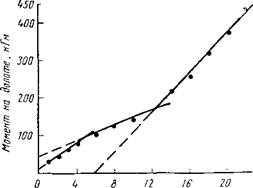
Осевая нагрузпа на долото, тс Рис. 5. Зависимость момента на долоте МЛ — от осевой нагрузки на долото G, построенная по данным [64] (долото № 1 модели ДЗСГЗЛИР-394, «=127 об/мин, глинистая пачка нижнего апшерона). Точки — фактические данные, линии — аппроксимация практических данных в соответствующих интервалах изменения G. |
Весьма распространенная ошибка при расчетах момента и мощности на долоте заключается в том, что на основе внешнего сходства эмпирической формулы (39) с аналитическим уравнением (36) считается, что величина С0 в формуле (39) представляет собой момент на долоте, потребный "на холостое вращение последнего. В действительности же Со (как и а) является параметром уравнения корреляционной связи момента на долоте с осевой нагрузкой на долото. Даже для одних и тех же условий, но для разных интервалов изменения осевой нагрузки на долото величины Со и а могут иметь различные значения. Сказанное хорошо иллюстрируется линиями на рис. 5.
В зависимости от того, для какого диапазона изменения С получена эмпирическая формула (39), С0 может быть больше или меньше М0, причем указанное различие может быть существенным (очевидно, может иметь место и равенство между С0 и М0); для разных диапазонов изменения осевой нагрузки на долото будут разными и значения величины а.
Для большинства практических расчетов знание величины момента MQ не является необходимым. Определение же этого момента в промысловых условиях весьма затруднительно. В буровой практике следует находить корреляционные уравнения связи [31]
|
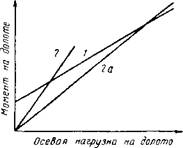
Рис. 6. Две зависимости, выражающие связь между моментом на долоте и осевой нагрузкой на долбто. / — по формуле (39); 2 и 2, а — по формуле (41). |
между моментом на долоте и осевой нагрузкой на долото вида (39) для определенных услр — вий при практически необходимых диапазонах изменения осевой нагрузки на долото (зачастую нет необходимости проводить промысловые эксперименты для низких значений осевой нагрузки на долото). Поэтому необходимо внести соответствующие указания, в методику проводки опорно-технологических скважин.
Чем больше Со отличается от нуля, меньше а и щире дна- пазон изменения осевой нагрузки на долото, тем больше по — ; грешность определения момента на долоте, получаемая при йс — пользовании одночленной формулы (41) вместо двучленной (39), ‘ что ясно видно из рис. 6. г