РЕАКЦИИ ОПОР ВЫШКИ ПРИ НЕБЛАГОПРИЯТНОМ СОЧЕТАНИИ АКТИВНЫХ СИЛ НА ОПРОКИДЫВАНИЕ
РЕАКЦИИ ОПОР ВЫШКИ ПРИ НЕБЛАГОПРИЯТНОМ СОЧЕТАНИИ АКТИВНЫХ СИЛ НА ОПРОКИДЫВАНИЕ
При бурении сравнительно глубоких разведочных скважин используют стационарные вышки, устанавливаемые на основании. В процессе их эксплуатации могут возникнуть самые разнообразные сочетания внешних активных сил. Из этих сочетаний выбирают неблагоприятные^ и для них рассчитывают опорные реакции и усилия в элементах вышки.
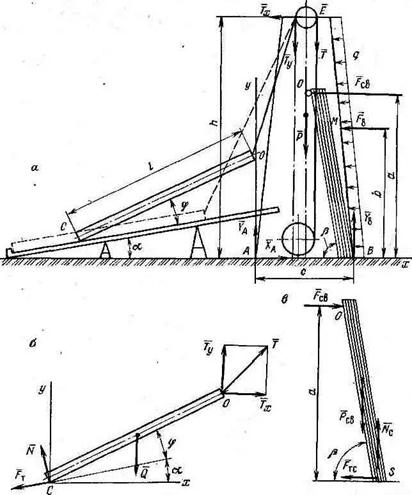
Одно из неблагоприятных сочетаний—такая комбинация активных сил (рис. 4.5), которая создает наибольший опрокидывающий момент или наибольшую горизонтальную составляющую реакции заделки. На рис. 4.5, а показана расчетная схема вышки для указанного
87
|
Рис. 4.5. К расчету буровой вышки на опрокидывание при неблагоприятном сочетании активных сил |
сочетания сил. Сущность задачи может быть сформулирована следующим образом. Лебедкой бурового станка поднимается обсадная труба длиной /, уложенная на козлах. Труба опирается нижним концом в точке С на негладкую наклонную плоскость. Коэффициент трения свечи о плоскость (настил на козлах) равен /, плоскость козел образует с горизонтальной плоскостью угол а. Труба с плоскостью козел образует угол ср, который в процессе подъема трубы изменяется от нуля до 90° — а. Внутри вышки под некоторым углом р установлен пакет свечей бурильных труб, который опирается на 88
вышку в точке О, расположенной от нижней плоскости вышки на расстоянии а. В процессе подъема трубы на вышку со стороны правой панели действует ветровая нагрузка интенсивностью q, равнодействующая FB этой нагрузки приложена в точке М, расположенной на расстоянии b от нижней плоскости вышки. Расстояние между точками закрепления вышки А и В равно с. Необходимо определить реакции опор вышки, считая, что в точке А неподвижная шарнирная заделка, а в точке В—подвижная шарнирная заделка. При расчете размерами блока можно пренебречь и считать, что силы Ту и Т направлены вдоль оси вышки.
Первоначально рассмотрим равновесие обсадной трубы (рис. 4.5, б), имея в виду, что для предельного случая Fr = Nf:
£/** = 0. Тх—TVsina—Vy/eosa=0; (4.46)
£/^,, = 0, Ncosa—Л/sina—Q+Ty = 0; (4.47)
£wc(F*)=0, Q cos (cp+a) // 2—Л7 cos a cos (cp+a)—
— N1 sin a sin (cp + a)—Nflcos a sin (a+ф)+Nfl sin a cos (ф + a) = 0. (4.48)
Из равенства (4.48) находим
О cos (ф + сс)
N-——————————— —’ ‘ . (4.49)
TOC o "1-5" h z 2 cos(ф +a)(cosa—/sina)+sin^-fa)(sina-f/cosa) ‘
Затем из равенства (4.46) можно определить
. T=Q______________ cos (ф+a) (sin a +/ cos a)___________
" 2 cos(ф+a)(cosa—/sinoc)+sin^+a)(sina-|-/cosa)
r==/v,_£_____________ cos (Ф+a) (/sin a—cos a)_________ ^
y ^ 2 cos (ф+a) (cos a —/sin a)+sin (ф+a) (sin a +/cos a)………………….. f
>
Зная Tx и Ty, можно вычислить
Т={Тх2+Туг)1’2. (4.52)
При а=0 (т. е. когда труба перед подъемом располагается
горизонтально)
. г О cos ф
Tcos<p+j! si. i<p’ ’
Т, Л ■ (4.54)
2 совф-Ь/вша
О cos ш
Ty = Q-~————— —• (4.55)
2 совф+уыпф
Максимальное значение горизонтальная составляющая натяжения каната приобретает, когда ф = 0:
Tx = Qfl 2. (4.56)’
Вертикальная составляющая натяжения каната в этом случае будет?; = е/2. (4.57)
Из соотношений (4.54) и (4.55) можно сделать важный дм практики вывод: как горизонтальная так и вертикальная составляющие натяжения каната не зависят от расстояния, на которое обсадная труба удалена от буровой вышки. Однако здесь важно сделать одну существенную оговорку. Для равновесия трубы, расположенной под углом ф (или ф + а при наличии козел), линия натянутого каната должна строго совпадать с направлением усилия Т. Достаточно немного натянуть канат и равновесие немедленно нарушится, а труба с ускорением устремится в сторону вышки. Бурильщики, использующие лебедку станка для подтаскивания к вышке различного оборудования, в том числе обсадных труб, хорошо знают, что эту операцию необходимо осуществлять чрезвычайно осторожно. При резком натяжении каната подтаскиваемая труба со значительным ускорением начнет двигаться к вышке и может стать причиной поломок станка или вышки.
Статически задачу о движении подтаскиваемой трубы решить невозможно. Она решается методами динамики. Однако отметим, что ее строгое решение осуществить затруднительно из-за невозможности точного задания усилия натяжения каната (приложенного в точке D).
Для рассмотрения условий равновесия вышки необходимо определить давление FCB на вышку со стороны пакета свечей (рис. 4.5, в). Поскольку в определении усилий FTC (сила трения пакета свечей о пол) и Nc (нормальная реакция пола) нет необходимости, воспользуемся уравнением моментов для определения только F,„. Условие равновесия будет иметь следующий вид:
I>s(Fk)=0, Fcn yCosP + FCBtf=0, (4.58)
где Рсв—сила тяжести пакета свечей; /св—длина одной свечи.
Тогда
Fob = FCB /св cos Р / 2а. (4.59)
Теперь можно рассмотреть условия равновесия вышки и определить искомые величины. Все действующие на вышку силы (активные и реакции связей) показаны на рис. 4.5, а. Составим одно из условий равновесия:
£*щШ=0- Txh-Tyc/2-Tc/2-Pc/2 + FCBa+FBb+YBc = 0. (4.60)
Составляем уравнение проекций сил на ось х:
|
Из уравнения (4.60) находим YB = (T^c+Tc+Pc-2Txh-2FBb)/2c. |
£F*,=0, XA-Tx-F„-FB= 0, (4.62)
откуда
Xa=T,+F^+Fb. (4.63)
! Наконец, составляем уравнение проекций сил на ось у
1^,-0, YA— Ту Т—Р + Уд=0 (4.64)
и определяем
YA=(TyC+ Tc+Pc+2Txh+2FCBa+2FBb)/2c. (4.65)
Вычисленные реакции применяют для последующего расчета оснований вышек. Для рассмотренного случая реакция YB может ■ оказаться отрицательной (вышка стремится опрокинуться относительно точки А). Тогда усилие YB используют для расчета якоря (анкера). Если укрепить вышку с помощью якоря не удается, то ее оборудуют канатными растяжками.
Рассмотрим числовой пример определения опорных реакций ног вышки для следующих исходных данных: 6=4000 Н, а=0, ф = 0, /=0,5, Рсв = 35000 Н, /св = 18,5 м, Р = 85°, с = 6 м, />=80000 Н, /г = 24м, а= 15 м, />=11 м, // = 60000 Н (вышка полностью обшита). После вычислений получаем Тх = (4000/2)0,5 = 1000 Н, 7^ = 2000 Н, 7"= 2240 Н, : FCB = 4700H, YB = —83 630 Н, ХА = 65 700 Н, YA= 167870 Н.
Все вычисленные реакции следует распределять между двумя, опорами. Обратим внимание на значительность горизонтальной 1 составляющей реакции опоры и отрицательный знак одной из вертикальных составляющих. Как показывает приведенный пример, I определяющей такое состояние нагружения вышки является ветровая I нагрузка.