ОСНОВНЫЕ ПОНЯТИЯ И СООТНОШЕНИЯ КИНЕМАТИКИ ТОЧКИ
ОСНОВНЫЕ ПОНЯТИЯ И СООТНОШЕНИЯ КИНЕМАТИКИ ТОЧКИ
Кинематикой называется раздел механики, в котором изучаются общие геометрические свойства движения точек и тел без учета их инертности (массы и распределения масс) и действующих на них силовых факторов.
Кинематика, с одной стороны, представляет собой введение в динамику, так как установление основных кинематических понятий 94 и зависимостей необходимо для изучения движения тел с учетом действующих сил. С другой стороны, методы кинематики имеют и самостоятельное значение, например, при изучении передач движения в буровых станках, насосах, двигателях, приборах, при исследовании движения породоразрушающих инструментов и вообще всех движущихся элементов в буровом оборудовании.
Как отмечалось, под движением в широком смысле понимается всякое изменение состояния материи. В кинематике, как и во всей механике, изучается только механическая форма движения, т. е. изменение с течением времени положения данного тела в пространстве относительно других тел. Механическое движение, как и любое другое, может существовать в пространстве и во времени.
Для определения положения движущегося тела (или точки) относительно другого тела, которое условно считается неподвижным, с последним жестко связывают какую-нибудь систему осей координат, которая называется системой отсчета. Если координаты всех точек тела в выбранной системе отсчета остаются все время постоянными, то тело по отношению к этой системе отсчета находится в покое. Если координаты каких-нибудь точек тела с течением времени изменяются, то тело по отношению к данной системе отсчета (а следовательно, и по отношению к телу, с которым эта система связана) находится в движении. В дальнейшем, говоря о движении тела по отношению к данной системе отсчета, под этим будет подразумевать движение по отношению к тому телу, с которым эта система отсчета связана.
Любое механическое движение может осуществляться в пространстве. Механика рассматривает движение только в абсолютном пространстве. Основные представления о таком пространстве сформулировал Эвклид (IV в. до н. э.). Написанный им труд «Элементы» содержит изложение основ стереометрии, т. е. пространственной геометрии. Эвклидово пространство трехмерно, однородно и изотропно.
Механическое движение невозможно представить без понятия время. Теоретическая механика оперирует универсальным временем. Это—скалярная величина, всегда положительная и изменяющаяся только в одну сторону.
В задачах кинематики время t обычно — независимая переменная величина (аргумент). Все другие переменные величины (расстояния, скорости, ускорения и т. д.) рассматривают как изменяющиеся во времени, т. е. как функции времени t. Отсчет времени ведется от некоторого начального момента (f=0), выбор которого в каждом случае оговаривают. Всякий данный момент времени определяется числом секунд, прошедших от начального момента до данного; разность между какими-нибудь двумя последовательными моментами времени называется промежутком времени.
Кинематика основывается только на аксиомах геометрии. Никакие другие аксиомы в кинематике не используют.
Для решения задач кинематики необходимо, чтобы изучаемое движение было каким-то образом задано (описано). Кинематически задать движение или закон движения тела (точки) означает задать положение этого тела (точки) в пространстве относительно данной системы отсчета в любой момент времени.
Основная задача кинематики состоит в том, чтобы, зная закон движения данного тела (или точки), определить все кинематические величины, характеризующие как движение тела в целом, так и движение каждой из его точек в отдельности (траектории, скорости, ускорения и т. д.). Для решения этой задачи необходимо, чтобы непосредственно был задан закон движения данного тела или закон движения какого-нибудь другого тела, кинематически связанного с данным.
Непрерывная линия, которую описывает движущаяся точка в пространстве относительно данной системы отсчета, называется траекторией точки:
Если траектория — прямая линия, то движение точки называется прямолинейным, в противном случае движение будет криволинейным. Для задания движения точки используют один из следующих трех способов: 1) естественный; 2) координатный; 3) векторный.
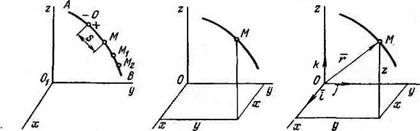
Естественным способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Схема, поясняющая естественный способ задания движения точки дана на рис. 5.1, а. Пусть точка М движется относительно системы отсчета Оi, х, у, z вдоль некоторой траектории АВ. Выберем на этой траектории какую-нибудь неподвижную точку О, которую примем за начало отсчета. Затем, рассматривая траекторию как обычную криволинейную’ координатную ось, установим на ней положительное и отрицательное направление, как на обычной координатной оси. Тогда положение точки М на траектории будет однозначно определяться криволинейной координатой s, равной расстоянию от точки О до точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М будет
|
Рис. 5.1. Схемы, поясняющие естественный (а), координатный (б) и векторный 1 (в) способы задания движения точки 1 |
■ перемещаться в положения М2, М2, —, М„, следовательно, расстояние будет с течением времени изменяться. Чтобы знать положение точки. на траектории (и, следовательно, в пространстве), в любой момент
|
|
(5.1)
Приведенное уравнение выражает закон движения точки М вдоль траектории. Криволинейная координата измеряется в единицах длины, чаще всего в метрах.
Функция s*=f(t) обладает следующими свойствами: она однозначна, непрерывна и дифференцируема. Однозначность определяется тем,
>■ что движущаяся точка не может одновременно находиться в двух ; местах на траектории; непрерывность отражает то обстоятельство,
; что точка не может «перескакивать» через некоторые участки траектории, а последовательно проходит все точки траектории; наконец, дифференцируемость указывает на то, что движущаяся точка [‘ должна обладать скоростью.
Заметим, что величина s в уравнении (5.1) определяет положение движущейся точки на траектории в данный момент времени, а не пройденный ею путь за какой-то промежуток времени. Например,
[ если точка, двигаясь из начала отсчета О, доходит до положения М2, а затем, перемещаясь в обратном направлении, приходит в положение М через М2, то в этот данный момент времени ее координата s равна дуге ОМ, а пройденный за время движения путь (уже за промежуток времени, но численно равный значению данного момента времени) будет равен дуге ОМ2+М2М, т. е. он не будет равен s. Криволинейная координата может быть положительной, отрицательной и равной нулю, путь—только положительным.
Стоит указать, что многие, начинающие изучать теоретическую механику, прежде всегр студенты, с трудом уясняют разницу между криволинейной координатой точки и пройденным ею путем, особенно при численном совпадении данного момента времени и промежутка времени.
В случае прямолинейного движения, если направить ось х вдоль, траектории точки, будет иметь s^x и закон прямолинейного движения точки может быть выражен в виде
|
(5.2) |
х —/(<)•
Пример. Пусть закон движения точки вдоль прямой имеет вид x=5+2t—4t2. Определить место нахождения точки в момент времени / = 2 с и пройденный ею путь за промежуток времени от 0 до / = 2 с. Для нахождения координаты достаточно в закон движения подставить t—2 с, тогда х=5+4—16=—7 м. Для определения пройденного пути возьмем от закона движения производную по времени и приравняем ее к нулю. Таким образом, мы определим значение момента времени, при котором функция, определяющая закон движения, достигает максимума:
dx/dt=2—Sti, ^ = 0,25 с.
|
1 |
7 3477
Найдем для этого значения времени координату точки s, = 3. Тогда пройденный точкой за t — 2 с путь будет соответствовать 3 + 3 + 7 = 13 м (три единицы в положительном направлении отсчета и 10 единиц в отрицательном направлении).
Естественный способ задания движения достаточно нагляден. Однако траектория точки заранее известна далеко не всегда. Поэтому на практике часто пользуются другим способом задания движения — координатным. Схема, поясняющая координатный способ задания движения точки, дана на рис. 5.1, б.
Положение точки М относительно данной системы отсчета х, у, 2 можно определить декартовыми координатами х, у, z. При движении все три координаты будут с течением времени изменяться. Чтобы выяснить закон движения точки, т. е. ее положение в пространстве в любой момент времени, надо определить значения координат точки для каждого момента времени, т. е. должны быть известны зависимости
|
(5.3) |
х=.1 (‘)’ >’=/(‘)’ z =/(‘)■
Уравнения (5.3) представляют собой уравнения движения точки в декартовых прямоугольных осях координат. Они определяют закон криволинейного движения точки при координатном способе задания движения. Координаты х, у и z измеряются в метрах.
Если движение точки совершается в одной и той же плоскости, то, приняв эту плоскость за плоскость Оху, мы получим в этом случае два уравнения движения.
Наконец, при прямолинейном движении точки, если вдоль ее траектории направить координатную ось Ох, движение будет описываться одним уравнением. Координатный и естественный способы в этом случае совпадают.
Уравнения (5.3) представляют собой одновременно уравнения траектории точки в параметрической форме, где роль параметра играет время t. Исключив из уравнений движения время t, можно найти уравнение траектории в обычной форме, т. е. в виде, дающем зависимость между ее координатами.
Схема, поясняющая векторный способ задания движения точки, дана на рис. 5.1, в. Пусть точка М движется относительно некоторой системы отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав вектор г, проведенный из начала координат О в точку М. Вектор г называется радиусом-вектором точки М.
При движении точки М вектор г будет с течением времени изменяться по модулю и направлению. Следовательно, г является переменным вектором (вектором-функцией), зависящим от аргумента:
(5.4)
|
Г |
Равенство (5.4) определяет закон криволинейного движения точки в векторной форме, так как оно позволяет в любой момент времени t построить соответствующий вектор г и найти положение движущейся 98
точки. Геометрическое место концов вектора г определяет траекторию движущейся точки.
Векторный способ задания движения удобен для установления общих зависимостей, так как позволяет описать движение точки одним векторным уравнением вместо трех скалярных.
При введении единичных векторов /, j, к, учитывая, что проекции вектора г йа оси х, V, г равны численному значению координат точки М, т. е. гх—х, /,. = у, /’, = получим
r = xi + vj+zk. (5.5)
, По этому уравнению можно для любого момента времени t построить вектор г и найти положение точки.
Одна из основных кинематических характеристик движения точки — векторная величина, называемая скоростью точки. При векторном способе задания движения вектор скорости определяется выражением
v = dr/dl. (5.6)
Вектор скорости в данный момент времени направлен по касательной к траектории точки в сторону движения.
Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Вектор ускорения точки определяется выражением:
w = dv/dt = d2r/dt2. (5.7)
В общем случае вектор ускорения располагается в соприкасающейся плоскости (из всех касательных плоскостей к точке М кривой соприкасающаяся плоскость имеет с кривой наибольший порядок соприкосновения, т. е. ближе других плоскостей «прилегает» к кривой) и всегда направлен в сторону выгнутости кривой.
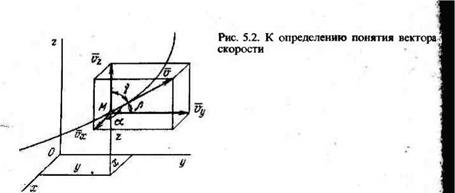
При координатном способе задания движения точки вектор скорости определяется через его проекции и направляющие косинусы (рис. 5.2):
vx=dx/dt, vy = dyjdt, iK = dz/dl, (5.8)
v=lvi + v(.+vi)112, (5.9)
v = vx + vy + vz = vxi+vj+ v, k. (5.10)
<x>sa — vx/v. cosP — Vy/v, cosY = r=/r, (5.11)
где ос, p. у — углы, составленные вектором скорости с положительными направлениями осей координат.
При этом скорость измеряется в м — с 1.
Вектор ускорения точки при координатном способе задания движения также ^определяется через его проекции на оси координат
и направляющие косинусы
wx=dvx/dt, Wy = dvyjdt, w, = dvz/clt; (5.12)
w=|u — + ir,2 + »rf)1,z; (5.13)
cosoci = h/h’, cosp! = wy/H’, cosYi = w,/w, (5.14)
7* 99
|
|
где at, pt, у j—углы, образуемые вектором ускорения с положительными направлениями осей координат; w—ускорение, м-с"2.
При решении задач кинематики прежде всего необходимо отыскивать, закон движения заданной точки (если этот закон сразу не задан в условиях задач). При отыскании этого закона по исходным данным ■ движущуюся точку, тело или механизм следует изображать в произволь — _ ном положении. Зная закон движения точки, можно определить любые’ другие кинематические характеристики движения (скорость, ускорение, ] время движения, пройденный путь за данный промежуток времени и т. д.)
Определим, как находятся векторы скорости и ускорения при естественном способе задания движения. Численная величина скорости точки в данный момент времени равна первой производной от криволинейной координаты точки по времени:
v = ds/dt. (5.15)
Вектор скорости направлен по касательной к траектории (которая при этом способе задания движения задается) в данной точке.
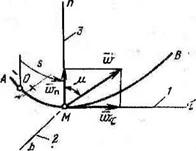
Приведенная формула определяет численную (алгебраическую) величину скорости. Если v > 0, то вектор скорости направлен в положительном направлении отсчета расстояния s, а если г<0, то в отрицательном. Схема естественного трехгранника и изображение касательного и нормального ускорения точки даны на рис. 5.3.
Вектор ускорения tv при естественном способе задания движения точки определяют по его проекциям на оси МхпЪ (см. рис. 5.3)Г имеющим начало в точке М и движущимся вместе с — нею. Эти оси, называемые осями естественного трехгранника, направлены следующим образом: ось т—карательная, или тангенциальная ось (1), вдоль касательной к траектории в сторону положительного отсчета криволинейной координаты; ось п—по главной нормали (3), лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось Ь—бинормаль (2), перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку.
Ранее говорилось, что ускорение точки w лежит*в соприкасающейся. плоскости, т. е. в плоскости Л/т л; следовательно, проекция вектора w на бинормаль всегда равна нулю (tvfc = 0).
‘ Рис. 5.3. Схема естественного трехгранника и изображение касательного И нормального ускорения точки
|
|
Касательная составляющая ускорения точки, характеризующая, изменения вектора. скорости во времени по численной, величине (модулю), определяется выражением
wz = dv/dl=d2s/dt2. (5.16)
Нормальная составляющая ускорения точки, характеризующая изменение вектора скорости во времени по направлению, определяется выражением
%=»а/р. (5-17).
где р—радиус кривизны траекторий в данной точке.
Полное ускорение точки
w=. Hw.+wtx’“. i (5.18)
, Направление вектора w характеризуется углом р, составленным вектором ускорения с нормалью:
tgH=|H>t|/w>„. (5.19)
Таким образом, если движение точки задано естественным способом, то, зная траекторию (а следовательно, и ее радиус кривизны в любой точке) и закон движения, можно по приведенным формулам определять модуль и направление векторов скорости si ускорения ■ точки в любой момент времени.