Бурение грунтовых зондов, установка энергетических колодцев

Движение систем материальных точек и твердых тел существенно зависит от распределения масс в системах и твердых телах. Общие теоремы динамики системы также учитывают распределение масс. Поэтому прежде, чем переходить к изложению общих теорем, приведем основные понятия о геометрии (или распределении) масс и количественных характеристиках распределения масс.

Механической системой материальных точек и тел будем называть такую их совокупность, в которой положение или движение каждой точки или тела зависит от положения или движения всех остальных. Любой двигатель, буровой станок, насос представляют собой типич­ные механические системы. Твердое тело мы тоже будем относить к системе материальных точек. Однако такая система обладает двумя отличительными свойствами. Во-первых, число материальных точек в твердом теле бесконечно, во-вторых, каждая точка твердого тела по отношению ко всем остальным находится в строго фиксированном положении. :

К величинам, характеризующим распределение масс систем, от­носятся: масса системы, координаты или радиус-вектор центра масс системы, моменты инерции относительно осей и центробежные моменты инерции.

Масса М системы равна арифметической сумме масс всех точек и тел, образующих системы. При этом выбор системы (т. е. включение в систему тех или иных точек и тел) зависит от характера решаемой задачи, т. е. является прерогативой исследователя.

Таким образом

М~^тк. (6.32)

Положение центра масс системы гс относительно данного начала отсчета определяется векторным выражением

гс=£/я*г*/Л/. (6.33)

Относительно заданных осей координат положение центра масс системы определяется выражениями (3.16).

Мерой инертности тела (или системы) при вращательном движе­нии, например, относительно оси г, является момент инерции тела относительно данной оси, или осевой момент инерции

(6.34)

где hk—расстояния от точек, входящих в систему до данной оси.

Момент инерции тела или системы относительно любой оси — величина положительная и не равная нулю.

Для вычисления осевых моментов инерции для системы матери­альных точек можно также пользоваться формулами

•fx = ‘£tf1k(yk+zk), Jv=) .тк{2к+Хк], Jz — ), тк ( Хк + )’к ), (6.35)

где хк, ук, zk—координаты точек системы.

Для сплошного однородного тела объемом V и плотностью р, ограниченного заданной поверхностью, момент инерции вычисляется по формуле —

4,= j p(x2+y2)dV. • (6.36)

(V)

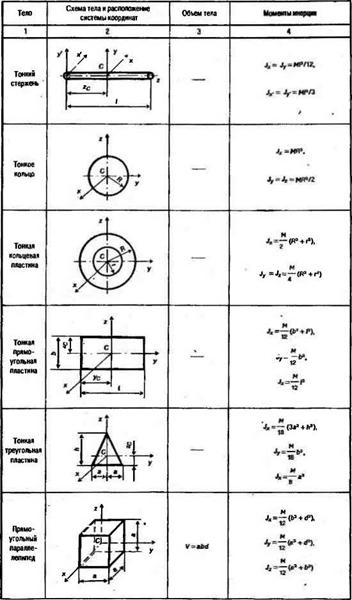
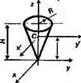
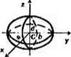
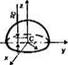
Объемы и моменты инерции некоторых однородных тел пред­ставлены в табл. 6.2. й

Часто момент инерции вычисляют через задаваемый в справоч­никах для различных тел радиус инерции ри:

‘ Jz=pLM. (6.37)

При вычислении моментов инерции относительно параллельных I осей часто пользуются теоремой Гюйгенса. Момент инерции тела относительно данной оси z равен моменту инерции относительно | оси zc, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния d между осями: 1

Jz=JzC+MdL. (6.38)

Следовательно, из всех осей данного направления наименьший момент инерции будет относительно той оси, которая проходит через центр масс.

Для характеристики асимметрии в распределении масс тела или тел вводится понятие центробежного момента инерции. Центробеж — s ными моментами инерции называются величины Jxy, Jyz и Jzx, определяемые равенствами ■

=У. ШкХкУк* J xz~ 7 . Ч^кУк ~к 1 Jzx )H}kZkXki (^*^9)

где тк—массы точек; хк, ук, zk-—координаты точек.

Очевидно, что Jxy=Jyx и т. д.

Для тел, ограниченных заданными поверхностями, формулы (6.39) приобретут вид

JX} — J yxydV и т. д. (6.40)

(У)

В отличие от осевых, центробежные моменты инерции могут быть ; как положительными, так и отрицательными, а при определенным? образом выбранных осях Oxyz могут обращаться в нули. Ось z, для — которой центробежные моменты инерции Jxy и Jyz, содержащие в своих ( индексах наименование этой оси, равны нулю, называется главной осью инерции тела. Если тело имеет плоскость симметрии, то любая ось, 1 перпендикулярная к этой плоскости, также будет главной осью инерции ‘ тела для точки О, в которой ось пересекает плоскость симметрии тела. 1 Если все центробежные моменты инерции равны нулю, т. е. Jxy = 0, : Jyz = 0 и Jzx = 0, то каждая из координатных осей системы отсчета Oxyz

является главной осью инерции тела для точки О (начала координат).

Через любую точку тела можно провести по крайней мере три такие взаимно перпендикулярные оси, для которых все три центробеж­ные моменты инерции обращаются в нуль и, следовательно, эти оси будут главными осями инерции тела. Главные оси, проведенные через центр масс тела, называются главными центральными осями инерции тела.

Объемы и моменты инерции однородных тел

Круговой цилиндр

V=n/(R*-Ra1)

= (Ra+R)+“-P.

ш

Круговой тор (г-радиус

*V 2 r-a

, 3 2(*(2r-a)-a»<4r-a), Jy = M[fla —r~—“

V=2n[5]R4(2f— 6)

R-рас сто* яние центра сечения от центра кольца)

= m|r

■»д=^=~м(на+-), 3 4=-MRa,

Круговой конус

Эллипсоид

(*М-

полуоси

эллипсоида)

Mr*

Полу шар

Примечание. Во всех случаях точкой с обозначены центры тажести фигур.

£ *

(> = £ mkvk.

(6-43)

(6.44)

Центробежные моменты инерции имеют ту же размерность, что

и осевые. 1 Осевые и центробежные моменты инерции играют огромную j роль в динамике систем материальных точек и твердого тела, в том числе в динамике бурового оборудования. Они используются при ;| балансировке оборудования, определении усилий, действующих на 1 подшипники и т. д.

Комментарии запрещены.