Бурение грунтовых зондов, установка энергетических колодцев

Новые технологии и устройства, конкурируя с уже имеющими­ся на рынке, не могут сразу занять значительную долю рынка из-за влияния большого числа факторов. Рассмотрим вопрос о том, каким образом происхо­дит внедрение инновационных товаров на рынок, т. е. как изменяется спрос на них с течением времени.

Пусть / — это часть максимального уровня внедрения, который может иметь новый товар на рассматриваемом рынке. С течением времени /увеличивается от нуля до значения, равного или меньшего единицы. После достижения уровня, равного единице, данная технология или устройство становятся «старыми» и их нужно заменять более новыми. В ходе замены старого изделия / уменьшается от единицы до нуля.

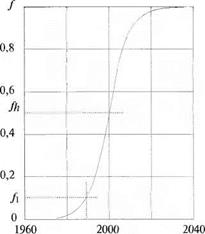
График/в зависимости от времени, построенный по эмпирическим данным, представляет собой S-образную кривую, представленную на рис. 1.5 (слева). Время внедрения на рынок АТ, определяется как АТ = (th — t{), где th — это вре­мя, за которое функция /становится равной 0,5 =/)|,и(1- это время, за кото­рое функция / изменяется от нуля до 0,1 = tv Величина АТ может иметь отри­цательное значение в том случае, когда данная технология устаревает и её за­меняют новой. В этом случае она называется временем вывода с рынка. Фишер

(Fisher, 1971) и При (Pry, 1973) показали, что зависимость /и

представляет собой линейную функцию, возрастающую с течением времени. На рис. 1.5 (справа) показано, как эмпирические данные коррелируют с данными,

полученными по теории Фишера-При. На данном графике представлена кривая внедрения на рынок сталелитейной технологии кислородного дутья в четырех различных странах. Прямые линии на графике изображают функцию, получен­ную по уравнению

где константы а и h характеризуют особенности рынка и конкретную техно-

1 d/

логию. Можно ожидать, что темп продвижения технологии на рынок, — —,

/ а/

будет пропорционален разности (1 — f) для участка, соответствующего началу продвижения на рынок:

(2)

Уравнение (2) полностью удовлетворяет эмпирическим данным графика 1.5 (справа) и данным, полученным из уравнения (1), поскольку последнее является интегралом первого.

США и Германия

1950 1960 1970 1980

Годы

Рис. 1.5. Типичная функция проникновения на рынок (слева). Функция внедрения новой сталелитейной технологии в различных странах (справа) по фактическим данным и по закону Фишера-При

Величины а и b зависят от самой технологии и от рынка, на который она вводится. В общем случае в уравнении Фишера-При можно избавиться от по­стоянных а и Ь.

Совместим полученные уравнения:

2 2

2,2 = a(th — /,) = a At, или а = ——

Таким образом, формула для функции проникновения новой технологии на рынок может быть записана в следующем виде:

(6)

Уравнение (6) представляет собой функцию от безразмерной независимой переменной (ґ — th)/At. Оно дает возможность отобразить данные для зависи­мостей с различными коэффициентами оиАна одном графике. Пример такого графика показан на рис. 1.6. Видно, что 17 эмпирических точек для различных продуктов и рынков имеют достаточно малый разброс относительно кривой Фишера-При.

На рис. 1.5 показана скорость внедрения метода кислородного дутья на рынках Японии (5 лет), Германии и США (6 лет) и СССР (8 лет). Скорость внедрения в некоторой степени зависит от особенностей страны, определяющих внедрение новых технологий (например, от особенностей технической политики и зако­нодательства в этой области), и от технических возможностей замены старых технологических ЛИНИЙ НОВЫМИ

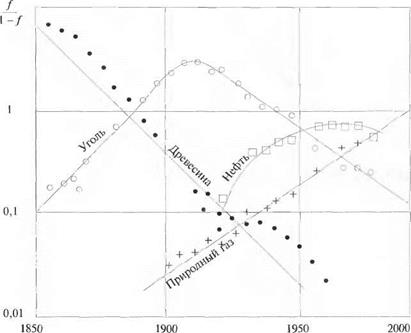
Закон продвижения новой продукции на рынок применим также и для энер­гетических технологий. На рис. 1.7 показано изменение предложения различ­ных источников энергии на рынке США. Из графика видно, как к концу XIX в. человек переходит от использования дров к использованию угля в качестве ос­новного топлива.

Уголь после достижения максимума использования в середине XX в. начинает вытесняться нефтью и природным газом. Как видно, ввод и вывод энергетиче­ских продуктов с рынка занимают гораздо большее время, чем для большинства остальных товаров и технологий. В табл. 1.3 показано характерное время про­движения и выведения с рынка различных источников энергии (время вывода имеет обратный знак).

J_ 1-/г 100

Рис. 1.6. График Фишера-При и эмпирические данные

Таблица 1.3. Время продвижения и вывода с рынка различных источников энергии Дерево -38 лет Уголь 38 лет Уголь -50 лет Нефть 30 лет

Таблица 1.4. Коэффициенты Фишера-При для дерева, угля и газа Энергоноситель а Ъ Дерево -0,0585 110,20 Уголь -0,0439 85,18 Газ -0,0426 -84,64

Рассмотрим период времени с началом в 1920 г. Дерево, уголь и природный газ характеризуются данными, полностью соответствующими модели Фишера — При. В течение этого периода потребление энергии, производимой гидроэлект­ростанциями, остается примерно постоянным и составляет около 3,6 % общего

энергопотребления. Регрессионные коэффициенты Фишера-При для древеси­ны, угля и газа имеют значения, приведенные в табл. 1.4. Поскольку для каж­дого момента времени ^ / = 1, часть рынка, занимаемая нефтью, может быть определена путем вычитания из единицы других частей рынка, относящихся к другим источникам энергии. График для нефти построен на рис. 1.7 с исполь­зованием именно такого подхода.

Голы Рис. 1.7. Изменение предложения различных источников энергии на рынке США в течение XIX и XX вв.

Коэффициенты Фишера-При были получены на основе данных за период с 1920 по 1950 гг., остальная информация — путем экстраполяции линейных зависимостей. Расчетная кривая для нефти показывает, что снижение по­требления нефти должно было начаться в 1970 г., что и случилось в действи­тельности. Чрезвычайно интересен тот факт, что снижение уровня потреб­ления нефти начиная с 70-х годов могло бы быть предсказано еще в 1950 г., т. е. до создания ОПЕК! Таким образом, можно прийти к выводу, что сни­жение потребления нефти должно было произойти независимо от действий ОПЕК! Создание ОПЕК повлияло лишь на уровень цен на нефть и другие энергоресурсы!

Комментарии запрещены.