Бурение грунтовых зондов, установка энергетических колодцев

Легко представить процесс сжатия, нарисовав зависимость дав­ления газа от его объема, как это сделано на рис. 2.2.

О Прим. ред. Уравнение р Vі = const называется уравнением адиабаты. Адиабатический процесс является частным случаем политропических процессов. Политропическим процессом называется процесс изменения состояния, при котором теплоемкость газа остается постоянной и равной dQ/d’l. Уравнение политропы имеет вид pV" = const, где п = (с — сД/(с — с). При dQ/dT = 0 п = с/с = у.

Р‘ V 1

Так как процесс обратимого сжатия есть результат большого числа последова­тельных равновесных шагов, то мы можем вычислить значения давления и объ­ема после каждого из этих шагов. На рис. 2.2 этот процесс представлен гладкой кривой. Отметим, что площадь замененной области под кривой соответствует работе, произведенной в процессе сжатия. Сжатие начинается с давления 1 МПа (при этом объем газа равен 100 литрам) и заканчивается при давлении 10 МПа (соответствующий объем 19,3 л).

ЗІ

С

Рис. 2.2. При обратимом адиабатическом сжатии переход из начального состояния А в конечное состояние С является плавным и предсказуемым. При быстром сжатии невозможно точно описать траекторию изменения

П> сть при быстром сжатии начальное состояние газа А совпадает с его на — іьньїм состоянием в предыдущем случае, а конечное состояние В характерн­ая тем же давлением (10 МПа), которое имел газ в результате медленного дія. В силу того, что в результате быстрого сжатия газ имеет более высокую лературу, он занимает больший объем (35,7 л вместо 19,3 л). При этом путь начального в конечное состояние не определен, на рисунке он условно обоз — н штриховой линией. В процессе быстрого сжатия давление и температу- не могут быть однозначно указаны, поскольку они неодинаковы по объему По мере того как поршень опускается, газ не успевает прийти в однород-

состояние.

Термины «медленное» и «быстрое» сжатие являются в какой-то мере услов­ными. В большинстве машин скорость процессов велика, тем не менее процес­сы сжатия или расширения с небольшой ошибкой можно считать достаточно медленными, чтобы предполагать однородное по объему распределение внут­ренних параметров.

Можно ли адиабатически сжать газ таким образом, чтобы при

расширении он вернулся точно в исходное состояние? Иными словами, может адиабатическое сжатие быть обратимым? Да, может, при условии, что сила прикладывается постепенно. Сжатие (или расширение) должно происходить в результате некоторого числа шагов, на каждом из которых газ остается в квази — новесном состоянии. Симуляцию такого процесса можно продемонстрировать численно достаточно простым способом, используя итерационный алгоритм. Стартуя с условий, которые мы имели в начале эксперимента, примем не — іьшое прирашение силы А/7так. что 7*7 = /7, + AF. Вычислим величину

(37)

числим 77 из выражения

Будем повторять процедуру до тех пор, пока 7*7 не станет равным FKQH. Здесь — конечное значение силы (в нашем примере 10 000 Н).

При достаточно малых значениях Дf получим, что /гкон = 0,0193 м и Ткон = 579,2 К. Кроме того, при расширении, осуществляемом таким же образом, мы вернемся к исходным значениям h, Vи Т. Итак, процесс обратим. Отметим, что конечное значение величины р Vу совпадае т с ее начальнвш значением. В действи­тельности pVy остается неизменным на всех шагах вычислений. Это не случайное совпадение. Позже в этой главе мы покажем, что для адиабатического обратимого процесса величина pV1 является константой. Далее мы также покажем, что этот так называемый политропический закон1′ применим ко всем адиабатическим про­цессам. Использование политропического закона позволяет рассчитать обратимый адиабатический процесс достаточно простым способом, не прибегая к итерацион­ной процедуре, которую мы использовали выше.

Результаты, полученные для обратимого адиабатического сжатия, приведе­ны ниже:

объем Иобр = 19,3 • 1 (У 6 м3, давление робр= Ю7 Па, температура 7^ = 579,2 К, высота Лобр = 0,0193 м,

Начнем с качественного описания процесса быстрого (скачко­образного) сжатия, а затем рассмотрим пример.

Предположим, что система, состоящая из цилиндра и поршня, находится в равновесии. Поршень, площадь поверхности которого равна А, расположен на высоте И0 от дна цилиндра, а объем, занимаемый газом, VQ = h0 А. Пусть сила[8]*, действующая на поршень, равна F0, так что давление газа р0 = F0 /А. Поршень жестко закреплен на месте и не может перемещаться. На него ста­вится дополнительный груз, что приводит к увеличению силы до значения Fy В какой-то момент поршень освобождается, что приводит к созданию давления на газ Ру = Fy /А, но газ еще находится при более низком давлении р0. Поршень начнет быстро опускаться и через некоторое время остановится на высоте Л, при этом давление газа будет равно рх. Над газом будет совершена работа Щ^х = /•’ (hQ — hy), и благодаря адиабатическим условиям эта работа полностью перейдет во внут­реннюю энергию газа, которая увеличится на AU= pcv(Tx — Т0). Сжатие приведет к уменьшению объема газа и увеличению его давления и температуры.

Если затем сила, действующая на поршень, примет прежнее значение, F2 = F0, то поршень поднимется вверх и окажется, что он находится на высоте h2 > h0. Температура газа при этом упадет от значения Тх, которое газ имел после сжатия, до значения Т2 > Т0. Система не вернется в исходное состо­яние по той причине, что сжатие газа происходило под действием силы Fx, а расширение — против меньшей силы F0. Таким образом, совершенная при расширении работа была меньше на велчину (W^y — Wx >2). В этом специфи­ческом цикле энергия была подведена извне. Следовательно, по определению, этот процесс необратим.

Пример

Рассмотрим адиабатическую систему цилиндр-поршень, изображенную на рис. 2.1. Пусть в ней находится р = 40,09 • 10-6 кмолей газа с у = 1,4 (у не зависит от темпера­туры). Температура газа Т0 = 300 К. Поперечное сечение цилиндра А = 0,001 м2. Поршень может перемещаться без трения, и на него действует сила F0 = 1000 Н. Следовательно, поршень создает давление р0 = FJA = 1000/0,001 = 106 Па.

Объем, который занимает газ,

Поршень находится на высоте h0 = VJA = 0,0001/0,001 = 0,1 м над дном цилиндра.

В равновесии давление газа равно давлению, которое на него оказывает поршень. Удельная теплоемкость газа при постоянном объеме

cv = = 20,785 Дж/(К • кмоль).

у-1

U0 = pc,.T(j = 40,09 -10-6 — 20,785 — 300 = 250 Дж,

Таким образом, фиксированные характеристики системы равны:

площадь А = 0,001 м2,

количество газа р = 40,09 ■ 10_6 кмолей,

гамма у = 1,4,

удельная теплоемкость газа при постоянном объеме cv = 20,785 ДжДК • кмоль).

Начальные значения параметров:

сила F0 = 1000 Н, объем VQ = 0.0001 м3, давление р0= 106Па, температура Г0 = 300 К, начальная энергия U{] = 250 Дж, высота h{] — 0,1 м,

ЛЛТ= 2,51.

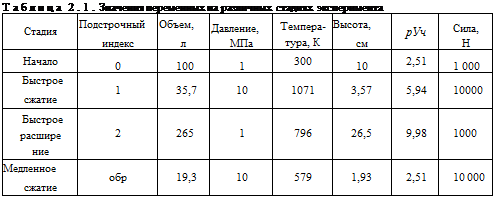
Ночные по всем стадиям процесса, рассмотренного в этом примере (приведены • ••эбт. 2.1).

і произойдет, если сила, действующая на поршень, резко (скачкообразно) уве — ится и станет равной 10 000 Н? Поршень опустится и остановится на высоте h{. действительности поршень сначала проскочит эту высоту и некоторое время будет эшать колебания около нее, перемещаясь вверх и вниз до тех пор, пока внутрен — потери в газе не приведут к затуханию этих колебаний.) В положении равновесия — ние газа станет равным:

Продолж. примера

При перемещении с высоты А0 на высоту А( поршень совершит работу И-^,

= т-М — (28)

Так как система является адиабатической, внутренняя энергия газа должна увели­читься на

д г/0 = pct, (7;-гс) = /;(/%-/!,), (29)

где 7’ — температура газа после сжатия,

Т _ рК _ piAhl _ 7, h 1 р7 xR pR 1

Подставляя выражение для 7, из (30) в уравнение (29), получаем

Решая (31) относительно А1? имеем

*1

Подставляя значения величин в (32) получаем, что А, = 0,0357 м. Объем газа после сжатия

К, = /1А, = 0,001 • 0,0357 = 35,7 ■ Ю"6 м3.

Температура газа

и произведение

рУ? = 107 (35,7 • 10 -6)1’4 = 5,94.

Таким образом, после сжатия мы имеем:

сила 7, = 10000 Н, объем Kj = 35.7 • 10-6 м3, давление Pj = 107 Па, температура 7, = 1071,4 К, высота А, = 0,0357 м,

^94-

Энергия, переданная поршнем газу,

W0_x = Fl{h0 — А,) = 10000(0,1 -0,0357) = 643 Дж. (36)

В этом примере мгновенно приложенная сила 10 000 Н (увеличение на 9000 Н) привела к возникновению сильно неравновесной ситуации. В момент, когда была приложена дополнительная сила, поршень производил давление Ю7 Па, в то вре-

Оконч. примера

мя как встречное давление газа составляло только 106 Па. Поршень очень быстро опустился в новое положение равновесия. Попытаемся обратить ситуацию, стартуя от полученных выше значений параметров, которые указаны также во второй строке табл. 2.1 (быстрое сжатие). Мы мгновенно уменьшаем усилие на 9000 Н (оставляя 1000 Н, которые имели первоначально). Вычисления, полностью аналогичные проделанным ранее, приводят нас к новым значениям искомых величин:

сила F2 = 1000 Н, объем V2 = 268 ■ 10_6 м3, давление р2 = 106 Па. температура Т2 = 795,6 К, высота И2 = 0,265 м.

Pi V? = 9,98.

Сила, действующая на поршень, равна первоначальному значению 1000 Н, но состо­яние газа далеко от того состояния, в котором он находился в начале эксперимента. Этого, как говорилось выше, следовало ожидать. Мы сжимали газ, прикладывая силу в 10 000 Н, а поршень поднимался вверх, преодолевая силу в 1000 Н. Несмотря на то что конечная высота больше, чем исходная, некоторая доля работы не восполнена. Дело в том, что внутренняя энергия газа теперь равна U2 = цс Т2 = 663 Дж. что на 413 Дж больше, чем начальное значение U0 = ре 70 = 250 Дж. Полученная разность значений внутренней энергии, естественно, равна разности между значениями

Для замкнутой системы, которую мы рассматривали до сих

мы вывели соотношение между внутренней энергией U, работой W оличеством тепла Q. Наиболее простой системой является система, в кото — сосуд с газом так хорошо теплоизолирован от внешней среды, что тепло ткуда не поступает и никуда не уходит. В такой адиабатической системе = 0. При перемещении поршня вниз работа, которую он совершает, пол­ью идет на увеличение внутренней энергии газа: AU = W. Сжатие газа но проводить настолько медленно, что в любой заданный момент време- давление, оказываемое поршнем, будет превышать давление газа на бес — чно малую величину. В этом случае процесс сжатия представляет собой еловательность квазиравновесных состояний и давление одинаково по

всему объему газа. Такая ситуация реализуется, например, когда поршень связан с шатуном механической тепловой машины. Возможно также быстрое (скачкообразное) сжатие, когда зафиксированный в некотором положении и нагруженный большим весом поршень внезапно освобождается. Тогда дав­ление газа непосредственно под поршнем быстро возрастает, но требуется определенное время для того, чтобы изменение давления распространилось по всему объему газа. Возникает неравновесная ситуация. Первый случай — медленное сжатие — является более общим и более важным. Тем не менее мы сначала рассмотрим вариант быстрого сжатия, потому что медленное сжатие можно трактовать как бесконечную последовательность бесконечно малых быстрых сжатий.

Комментарии запрещены.