 ТУРБИНЫ
ТУРБИНЫ
 |
 |
Турбина генерирует механическую энергию за счет использован! разности давлений. Обычно давление газа на входе и выходе турбины известно. Пусть рт и Тш — давление и температура на входе в турбину, а р(Ш и Тои,
![]() w = Hia-H(
w = Hia-H(
или
Предполагая постоянство теплоемкости, получим
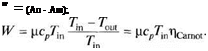 |
Ап — Аш( — ср (An — Amt) >
Приведенные выше соотношения напоминают соотношения, которые ра были получены для тепловых двигателей. Однако величина рсрТт, хотя и им размерность энергии, не является количеством тепла, подводимым к устройс а это — энтальпия газа на входе. При заданных условиях на входе и извест і : давлении на выходе вырабатываемая механическая энергия растет при сниже температуры на выходе. Минимально возможная температура на выходе оі ничивается вторым законом термодинамики, который требует, чтобы энтро выходящих газов была равна или больше, чем энтропия входящих газов. Ми
ьная температура на выходе реализуется, если турбина работает изоэнтро — ино. т. е. энтропия газа в процессе расширения не изменяется. Отклонения изоэнтропийности связаны с потерями и соответственно с выделением тепла, везет к повышению температуры на выходе.
Изоэнтропийные процессы
"Vouecc в турбине, протекающий без изменения энтропии газа, называется изоэн — тропийным.
.1 і первого закона термодинамики
|
dQ = dU + pdV, |
(7) |
|
из второго закона термодинамики dQ = TdS, |
(8) |
|
TdS = dU = pdV. |
(9) |
|
И і определения энтальпии как Н = U + pV, следует |
|
|
d U = dB — V dp-pdV. |
(10) |
|
іедовательно, TdS = dH — Vdp, |
Ш) |
|
TdS = — —dp T T |
(12) |
|
Ho dH= cpdTи V/T = R/p, следовательно |
|
|
d7′ dp d5 = c„—- R — ■ p T p |
(13) |
|
"win процесс является изоэнтропийным, то d, S’ = 0 и |
|
|
с ^L=r^=(c — с)*Р, ср т К р ср v> р |
(14) |
|
^TfUdp, т у) р |
(15) |
|
In 7 + р—-jlnp = const, |
(16) |
1-т
Тр у = const. (17)
И окончательно из уравнения идеального газа
pVy = const. (18)
Таким образом, подтропический закон, выведенный для случая адиабатического сжатия (см. гл. 2), применим для любого изоэнтропийного процесса
Чему равна температура газа на выходе из изоэнтропийной турбины? Используя политропический закон, получим
Рш Кг /’outpour
Применяя уравнение идеального газа, легко получить соотношения:
 Pl’PRT, l = AlutVl^out. min.
Pl’PRT, l = AlutVl^out. min.
Y-l
|
Т. = t out. mm *in |
ALut ] Y
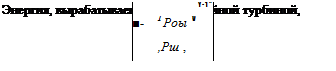 |
|
А Г
Турбина может рассматриваться как адиабатическая в том смысле, что п текаюгций через нее газ не обменивается теплом с окружающей средой. Одг ко такой процесс может быть связан с внутренними потерями, приводящим к повышению температуры газа на выходе. Она оказывается выше, чем д расчет по соотношению (21).
Изоэнтропийная эффективность турбины определяется как отношение v ально выполненной работы к работе, которая могла бы быть получена в изо’ тропийном процессе.