Бурение грунтовых зондов, установка энергетических колодцев

В первом приближении ЭХГ может быть рассмотрен в сопоставлении с некоторой теплосиловой установкой. В отличие от обычной теплосиловой установки в ЭХГ ре­акции между топливом и окислителем локально разде­лены (т. е. протекают на разных электродах); в системе отсутствует стадия выделения и превращения тепловой энергии. С термодинамической точки зрения последнее обстоятельство позволяет рассматривать ЭХГ как одно — 38

температурную систему (обычная теплосиловая установ­ка всегда, по крайней мере, двухтемпературная си­стема).

Соответственно этому изменяется и роль окружаю­щей среды, которая в зависимости от обстоятельств мо­жет быть как теплоприемником, так и источником тепло­ты (в обычной теплосиловой установке окружающая среда всегда теплоприемник). Последнее замечание оз­начает, что при определенных условиях часть энергии окружающего пространства может быть преобразована в электрическую.

Термодинамика обратимых, т. е. равновесных процес­сов без самопроизвольных реакций, позволяет опреде­лить несколько важных для практики параметров ТЭ, в том числе КПД г) и ЭДС Е0. Для описания равновес­ного процесса мы представляем ТЭ в виде двух электро­дов, находящихся в контакте с электролитом и соединен­ных внешней цепью. Под напряжением такого ТЭ будем понимать разность потенциалов между конечными ме­таллами, причем металлы эти должны быть одинаковы. Потенциал отдельного электрода может быть определен также по отношению к некоторому другому, названному электродом сравнения (за такой обычно принимают во­дородный электрод). Величина Лср=срі—qa—U и будет являться рабочим напряжением ТЭ.

Чрезвычайно важным является то обстоятельство, что хотя отдельные потенциалы ф, называемые внутренними потенциалами или потенциалами Гальвапи, мы измерять не можем (ф — потенциал внутри фазы, отнесенный к бесконечно удаленной точке в незаряженном вакууме, и при переходе через границу фаз необходимо учесть неизвестную работу по перемещению заряда), но раз­ность Дф поддается измерению. Равновесное состояние, характеризующее Дф=£’0, не является статическим: да­же при суммарном токе, равном нулю, происходит реак­ция на электроде, причем через границу осуществляется обмен носителями. Образующийся «равновесный» ток назван током обмена /о. Физически он характеризует скорость установления потенциала электрода и его чув­ствительность к нарушению равновесия. Нашей дальней­шей целью будет определение значения ЭДС.

Введем несколько термодинамических параметров, характеризующих поведение равновесного ТЭ [2.1, 2.2]. Во-первых, отметим, что ТЭ работает в изобарно-изотер­
мическом режиме. Это означает, что в нем давление и температура процесса — постоянные величины, p=const, Т = const.

Термодинамика позволяет описать такие процессы (с двумя постоянными параметрами системы) некоторы­ми так называемыми характеристическими функциями Ф. Основное достоинство этих функций — возможность расчета их изменения ДФ=гФі—Ф2 вне зависимости от «пути» процесса (математически это означает сущест­вование полного дифференциала йф). Таким образом, зная Фі и Ф2 в начале и конце процесса, можно вычис­лить АФ при любом характере изменения этого пара­метра. Для изобарно-изотермического процесса ДФ= =AG, где G — функция Гиббса или свободная энталь­пия. Можно показать, что максимальная полезная рабо­та L в системах с двумя постоянными параметрами рав­на изменению характеристической функции. Таким обра­зом, для изобарно-изотермической системы

AG=—L.

Функция Гиббса связана с энтальпией Н, температу­рой Т и энтропией S:

G—H—TS.

Отсюда (при p=const, T=const)

AG = AH—TAS. (2.1)

АН — называют тепловым эффектом реакции QT. Ве­личину AS можно определить как

Гд (АО)’

I дТ у

A G = AQ-T^’j = ~L. (2.2)

Величина AG связана с ЭДС Е0 простым соотноше­нием (одна из форм закона Фарадея)

AG=—nFE0, (2.3)

где п — число электронов на реагирующую молекулу или ион; F — число Фарадея (96500 Кл/г).

Тогда

Второй член правой части равен тёплотё, пбглощаё — мой (выделяемой) при работе ТЭ (эта величина отнюдь не равна Qr). В зависимости от знака (дЕ0/дТ)р, т. е. от характера реакции, возможны три вида ТЭ:

а) работающие с выделением теплоты во внешнюю среду Д5>0, Eo^Qr/nF;

б) без выделения или поглощения теплоты (адиа­батический режим) AS=0, Eo—Qt/hF;

в) с поглощением теплоты из внешней среды Д5<0, E0<QT/nF.

2.1. РАСЧЕТ КПД И ЭДС

Идеальный термический КПД ТЭ есть отношение максимальной полезной работы к тепловому эффекту реакции:

(2.5)

После подстановки выражения (2.1) имеем

, т as /0

Ъ 1 а н • (2-6)

Рассмотрев три случая взаимодействия ТЭ с окру­жающей средой (выделение теплоты и ее поглощение, а также адиабатический режим), получим три возмож­ных значения идеального КПД: тр<1; тр = 1; тр>1.

Как и для случая Е0, КПД определяется величиной

Физически значение КПД больше единицы означает использование для получения работы не только химиче­ской энергии реагентов, но и энергии окружающей среды.

Истинный КПД ТЭ зависит от ряда факторов и мо­жет быть представлен в виде

Г|=тіпітТ]сг, (2.7)

где ці — КПД по току, который отражает соответствие закону Фарадея данной реакции (неполное использова­ние реагентов). Этот КПД равен отношению фактически полученного электричества к теоретически возможному:

гц=(/гК)ист/«К;

Ци — КПД по напряжению, который связан с необра­тимыми потерями в ТЭ (см. ниже) и отражает отличие

йёравновесного процесса от равновесного: тщ=£//До, где U — напряжение на ТЭ.

Предположим, что активные вещества — идеальные газы с постоянной теплоемкостью (учет отклонения от идеальности и переменности теплоемкостей не представ­ляет принципиальных трудностей) [2.3]. Тогда, учиты­вая, что = #,*„ +Т, а давление и температура постоянны, имеем

QP = — + T2v<c№;); v. ~ ~ ; Vv. l =

= -ЪДТ1р,

где V, —стехиометрические коэффициенты, входящие в уравнение химической реакции между активными ве­ществами 2v, S(—0.

Обозначим

-2л>гЯ /р = а; -Sv, c /p = fc,;

r/0

— 2v;/p = A.

Тогда

Q„/p=a + W; b=b=ARrTlp-

Подставив полученное значение QP/p в уравнение для ЭДС, получим

■ Е’^а + ьт + т^)’.

В результате интегрирования по Т (при p=const) получим

Е0=а—ЬТп T + Tf(p). (2.8)

Произвольная функция давления f(p), появившаяся при интегрировании по Т, определяется на основании

‘(w)r = V-~V* T^=ARrTlf

и, следовательно, f (p) = ARn pi р„.

г*

Таким образом, ЭДС газового ТЭ равна

Из полученного выражения для Е0 видно, что с из­менением температуры Д0 проходит через максимум;

температура Т *, при которой Е0 достигает максимума, определяется из условия

— b — b In Т + AR In р’р, = 0.

Термический КПД элемента с изменением темпера­туры проходит через максимум, достигаемый при темпе­ратуре Т„.ах, который определяется условием

— 2ab — b2Tmax — ah In Tmax + aAR In p/p0 = 0.

Так как отношение b/а положительно, то максималь­ное значение термического КПД ТЭ всегда больше еди­ницы. Так же как и Е0, КПД ТЭ меняется в зависимо­сти от давления монотонно (при Sv,<0 увеличивается и при 2v, X) уменьшается).

Проведенный анализ относится к случаю работы ТЭ при температуре, равной температуре окружающей сре­ды. Поскольку это условие, вообще говоря, необязатель­но, рассмотрим особенности работы ТЭ, обусловленные неравенством температур ТЭ Т и окружающей среды Т.

Предположим вначале, что Т~>Т’. Тогда для того, чтобы все процессы были обратимы, необходимо, чтобы между температурами Т и Т’ действовала тепловая ма­шина Карно, обеспечивающая обратимый перенос теп­лоты от ТЭ к окружающей среде (когда теплота выде­ляется в ТЭ) или от окружающей среды к ТЭ (в случае поглощения теплоты ТЭ).

Из условия обратимости процесса Д5*=0 имеем S2—5]—Ql>2/T’—0 и соответственно

При выводе формулы для термического КПД надо учесть работу тепловой машины, переносящей теплоту Qo6pi-2 от окружающей среды к ТЭ или обратно. Эта ра­бота равна (Т—Т’)Т~1 (Q°6p,.2 77F).

Таким образом, общая работа

F —Qp — T (5, — S2) — Q^P Г ~r! ‘-

a термический КПД

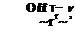7jf = 1 — (5,—S2)

Заменив 5, — S2 через — Q°62p /V, получим, , Qf-2 t t— г, ,

ъ + Qp T’ Qp T’ + % •

где Qi-2 считается положительным, если теплота посту­пает от окружающей среды к ТЭ, и отрицательным, если теплота отдается ТЭ окружающей среде.

Используя (2.12), выражение для тц можно предста­вить также в следующем виде:

^ = (2.13)

Полученные формулы для rt относятся к тому слу­чаю, когда все процессы как в самом ТЭ, так и при теп­лообмене с окружающей средой обратимы.

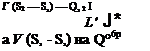Если процессы необратимы, то полезная работа будет меньше на V AS*, где AS*=S2—Si—Qi-2/T’, и соответ­ственно действительный КПД ТЭ

(2.15)

Выразив далее Q^2P jQ„ через it— 1, получим оконча­тельно ■>]= 1 -)-QN2/Qp. Общая производимая работа

L = Qp-T(Sx — S9) + Q*p (Г — T)jV. (2.16)

Так как выражение для L’ остается для T<iT’ тем же самым, что и в случае Т>Т’, приведенные выше формулы для ці ит] имеют самое общее значение. Ис­следованием выражений для ЭДС и термического КПД исчерпываются результаты анализа равновесных процес­сов в ТЭ.

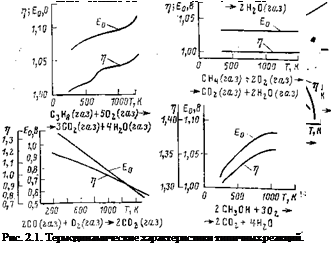Результаты непосредственных расчетов ЭДС и КПД ТЭ, выполненных по приведенной методике для наибо-

лее интересных веществ, представлены на рис. 2.1. Ана­лиз полученных соотношений, рассматриваемых в каче­стве каталога возможных реакций, позволяет в первом приближении оценить оптимальный температурный диа­пазон для выбранных исходных продуктов ТЭ.

Комментарии запрещены.