 Модели переноса заряда на границе электрод — электролит
Модели переноса заряда на границе электрод — электролит
В этом подпараграфе будет рассмотрена одна из важных проблем катализа — изучение причин переноса заряда через границу раздела сред: электрод (металл) — электролит.
Как уже отмечалось, процесс генерирования и переноса заряда через границу, включая преодоление энергетических барьеров, происходит во многих моделях ТЭ
при относительно низких температурах (например, в во- дород-кислородном ЭХГ 50—70°С), когда обычно рассматриваемые в физике твердого тела процессы эмиссии электронов нереальны.
Откуда же создается ситуация, обеспечивающая заряду возможность преодоления энергетического барьера через межфазовую границу? К сожалению, ответа, удовлетворяющего физической причинной схеме, пока получить не удается.
Возможные механизмы кинетики рассматриваются ниже.
Одна из первых феноменологических моделей была развита Хориучи и Поляни. Она позволяла объяснить
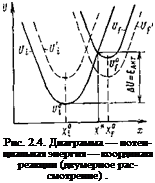 ряд основных закономерностей кинетики: зависимость скорости реакции от потенциала и энергии адсорбции промежуточного продукта реакции. При этом подходе выделяют некоторую координату реакции X, от которой зависит энергия системы В начальном состоянии энергия U°i минимальна около некоторого значения Х°{, в конечном—минимальна, U°f при X°f. Поскольку X°i, X°f не совпадают, две потенциальные кривые U—f(X) пересекаются в точке X* — возникает барьер высотой А(7= = U*—U°u который отождествляется с энергией активации (рис. 2.4). Сделанные предположения означают допущение чисто классической картины надбарьерного перехода системы из начального состояния в конечное. Повышение перенапряжения (сдвиг начальной кривой вверх — пунктирная кривая £/’,■) или увеличение энергии адсорбции (пунктирная кривая U’f) приводят соответственно к снижению энергии активации. Широкий круг важнейших закономерностей кинетики в этом приближении носит чисто феноменологический характер и не связан с тонким физическим смыслом X, т. с. с конкретным механизмом процесса. Современное развитие теории элементарного акта связывается с советскими работами (Р. Р. Догонадзе и др.) [2.6]. Более глубокий анализ 58
ряд основных закономерностей кинетики: зависимость скорости реакции от потенциала и энергии адсорбции промежуточного продукта реакции. При этом подходе выделяют некоторую координату реакции X, от которой зависит энергия системы В начальном состоянии энергия U°i минимальна около некоторого значения Х°{, в конечном—минимальна, U°f при X°f. Поскольку X°i, X°f не совпадают, две потенциальные кривые U—f(X) пересекаются в точке X* — возникает барьер высотой А(7= = U*—U°u который отождествляется с энергией активации (рис. 2.4). Сделанные предположения означают допущение чисто классической картины надбарьерного перехода системы из начального состояния в конечное. Повышение перенапряжения (сдвиг начальной кривой вверх — пунктирная кривая £/’,■) или увеличение энергии адсорбции (пунктирная кривая U’f) приводят соответственно к снижению энергии активации. Широкий круг важнейших закономерностей кинетики в этом приближении носит чисто феноменологический характер и не связан с тонким физическим смыслом X, т. с. с конкретным механизмом процесса. Современное развитие теории элементарного акта связывается с советскими работами (Р. Р. Догонадзе и др.) [2.6]. Более глубокий анализ 58
как свойств полярной среды, так и характеристик ковалентной связи позволил подойти к созданию квантовой теории элементарного акта реакций с переносом заряда.
 Эту теорию отличают две особенности. Во-первых, наряду с движением переносимой в ходе реакции частицы (электрон, протон) учитывается движение дипольных молекул растворителя. Энергия взаимодействия заряженной частицы с растворителем составляет несколько десятков килоджоулей на моль. Это означает, что энергия активации сильнозависит от поляризационного состояния растворителя. Характерной чертой является и то, что растворитель рассматривается как динамическая система, активно участвую щая в ходе элементарного акта. Второй особенностью развиваемой теории является последовательное применение квантовомеханического описания для всех видов молекулярного движения, сопровождающих реакцию. Дело обстоит так, что тот или иной вид движения (степень свободы) существенно зависит от его количественных характеристик.
Эту теорию отличают две особенности. Во-первых, наряду с движением переносимой в ходе реакции частицы (электрон, протон) учитывается движение дипольных молекул растворителя. Энергия взаимодействия заряженной частицы с растворителем составляет несколько десятков килоджоулей на моль. Это означает, что энергия активации сильнозависит от поляризационного состояния растворителя. Характерной чертой является и то, что растворитель рассматривается как динамическая система, активно участвую щая в ходе элементарного акта. Второй особенностью развиваемой теории является последовательное применение квантовомеханического описания для всех видов молекулярного движения, сопровождающих реакцию. Дело обстоит так, что тот или иной вид движения (степень свободы) существенно зависит от его количественных характеристик.
Так, если частота колебаний реагирующей степени свободы по соответствующей координате мала (энергит колебательного кванта Ды <С&Г), то степени свободы ведут себя «классическим» образом, т. е. переход по этой координате из начального состояния в конечное проходит над барьером. Если же частота колебаний велика, то необходимо учесть для этой степени свободы конкуренцию двух путей перехода: н. адбарьерного и подбарьерного. При Н(л~Э>кТ поведение соответствующей степени свободы становится существенно квантовым, поэтому подбарьерный переход становится наиболее вероятным.
С точки зрения теории Догонадзе электрохимическая реакция передачи заряда (например, разряд донора-про — тона) протекает следующим образом. Сначала в результате тепловых флуктуаций происходит изменение поля
ризации растворителя и ориентации диполей в реакционной сфере. Это движение носит классический характер, и вероятность достижения той или иной конфигурации диполей определяется по формуле Больцмана — по отклонению энергии системы в этом состоянии
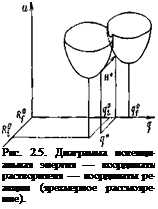
![]() от ее равновесного значения I, вероятность W ^е При некотором значении q* координаты растворителя (рис. 2.5) энергия исходного состояния оказывается равной энергии конечного состояния. Равенство энергий начального и конечного состояний означает, что в этот момент становится возможным надбарьерный переход из исходной потенциальной ямы в конечную. На рис. 2.5 изображены поверхности потенциальной энергии начального и конечного состояний как функции координат растворителя q и координаты реакции R. Стрелкой отмечено туннелирование протона, происходящее при постоянной энергии и координате растворителя q*.
от ее равновесного значения I, вероятность W ^е При некотором значении q* координаты растворителя (рис. 2.5) энергия исходного состояния оказывается равной энергии конечного состояния. Равенство энергий начального и конечного состояний означает, что в этот момент становится возможным надбарьерный переход из исходной потенциальной ямы в конечную. На рис. 2.5 изображены поверхности потенциальной энергии начального и конечного состояний как функции координат растворителя q и координаты реакции R. Стрелкой отмечено туннелирование протона, происходящее при постоянной энергии и координате растворителя q*.
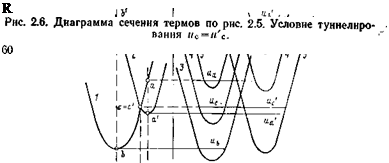
На рис. 2.6 в левой части изображены потенциальные кривые в функции q. Кривая 1 — при постоянном R, равном его равновесному начальному значению R°i, кривая 2 — при R—R°f. Кривые 1 и 2 представляют собой сечения соответствующих параболоидов на рис. 2.5 плоскостями R=R°j, Rz=zR°f. Эти две кривые спроектированы на одну плоскость. В правой части рис. 2.6 изображены кривые и в функции R при #=const. Кривые 3 и 3′ соответствуют равновесному q в начальном состоянии q°i, 4
U.
и 4′ — q°h 5 и 5’—q*, соответствующему пересечению
кривых в левой части рис. 2.6. Только для пары 5 и 5′ нулевые уровни протона выровнены, т. е. только в этом случае возможно туннелирование.
Развитые представления позволяют сформулировать вероятность элементарного акта, используя положения кваитовомеханической теории реакций. Согласно этой теории вводятся представления о входном и выходном каналах реакции, характеризуемых соответственно гамильтонианами и волновыми функциями Н и VF. Гамильтонианы
Ні + Vi и Hf + Vf (2.34)
включают только энергию невзаимодействующих реагентов во входном и выходном каналах. Функции Y/, 4*7 удовлетворяют уравнениям
Н№1=Е№ HfWf=EfWf. (2.35)
Функции Vi и Vf описывают взаимодействие реаген
тов во входном и выходном каналах.
В зоне реакции, где происходит элементарный акт, состояние системы не является стационарным, его следует рассматривать согласно временному уравнению Шре- дингера. Гамильтониан имеет двоякий вид
H=H,+ Vi=Hf+Vf. (2.36)
При решении необходимо принять во внимание, что до элементарного акта волновая функция совпадала
с ‘Г,-. Вероятность перехода дается выражением
Wlf = ■^ £ I< w, х | ■ЧГг > I г5 (Et — Е[) e~Eil*Tz-]. (2.37)
if
Суммирование проводится по состояниям конечного канала, и усреднение проводится по Гиббсу по состоянию начального канала.
Оператор перехода имеет вид
^ = Vi+VfWF^rTfdVi, S^O. . ■ (2.38)
Если взаимодействие реагентов слабое, то становится справедливым борцовское приближение теории реакций. Формула (2.38) приобретает более простой вид
w‘f = ■X £ 1 < WiГv‘’ ^ > Г8 — Er) e’El, kTz-
if ■
V:. . : ‘ 4 . ‘ ‘% І’ Ь (2.39)
‘. " * ■*’ С1
Фактический расчет вероятности перехода в наиболее общем виде был проведен в [2.6] на примере реакций переноса электрона. Для вероятности элементарного акта в единицу времени было получено выражение
где Vif — матричный элемент перехода; ег(ю)—относительная диэлектрическая проницаемость; е",- (со)—ее мнимая часть; В — энергия «реорганизации» среды,
 |
где D — индукция электрического поля.
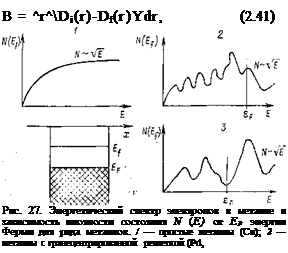
Pt); 3 — металлы с объемно-центрированной решеткой (W).
![]() N {Е ) = lim ь ДЯ-+0
N {Е ) = lim ь ДЯ-+0
Гетерогенные реакции, протекающие на электродах, являются одним из видов рассмотренных выше процессов, и к ним полностью применимы изложенные выше представления. Спецификой данного случая является наличие электрода и необходимость его описания.
На рис. 2.7 изображена структура энергетического спектра электронов металлического электрода, а также плотность состояний для некоторых металлов. Характерной чертой является непрерывный энергетический 62
спектр, характеризуемый плотностью уровней р (Ef) (Ef — энергетический уровень электрона, участвующего в реакции) и числом заполнения n(Ef) в соответствии с распределением Ферми —Дирака
где Ef — энергия электрона на уровне Ферми.
Вероятность перехода в данном случае характеризует ток элементарного акта, который определяется формулой
і = еСУ f п (Е,) р (Ef) Wif (Ef) dEj, (2.43) где C‘o — концентрация ионов; V’ — реакционный объем.
Теория Догонадзе является весьма общей и позволяет рассмотреть большое число процессов с единой точки зрения. Однако следует заметить, что не все случаи, встречающиеся на опыте, исчерпываются этой теорией. Характерным примером является реакция адсорбции, адекватное описание которой оказалось более сложным. Еще раз подчеркнем, что все изложенное выше относится к одночастичному приближению и не отражает фактическую картину сложных коллективных моделей переноса заряда в реальных системах.