Энергия ветра
Энергия ветра
Строго говоря, все виды возобновляемых энергоресурсов Земли взаимосвязаны и имеют общее происхождение от солнечной энергии. Общей теории современных возобновляемых энергоресурсов планеты пока не создано. Подход к независимой оценке потенциала конкретного энергоресурса имеет условный детерминированный характер, позво
ляющий определить масштабы и условия его практического использования.
Ветер характеризуется скоростью, являющейся случайной переменной в пространстве и времени. Поэтому, на современном уровне исследований, энергетические характеристики ветра представляются вероятностным описанием случайного процесса изменения ветроэнергетического потенциала. Основой вероятностного подхода является дискретизация временного процесса, позволяющая считать независимыми и постоянными все определяемые параметры на интервале дискретизации. В качестве временных интервалов стационарности обычно используется час, сутки, сезон, год.
Совокупность аэрологических и энергетических характеристик ветра объединяется в ветроэнергетический кадастр региона. Основными характеристиками ветроэнергетического кадастра являются:
• среднегодовая скорость ветра, годовой и суточный ход ветра;
• повторяемость скоростей, типы и параметры функций распределения скоростей ветра;
• вертикальный профиль средней скорости ветра;
• удельная мощность и удельная энергия ветра;
• ветроэнергетические ресурсы региона.
Для получения достоверных данных о средних скоростях ветра территории необходимо использовать значительные объемы измерений в течение достаточно длительного времени. В литературе [18] приводятся рекомендации о целесообразности 10-летних объемов выборки наблюдений.
Среднегодовая скорость ветра определяется как среднеарифметическое значение, полученное в результате измерений скорости через равные промежутки времени в течение заданного периода: сутки, месяц, год, несколько лет:
где V — скорость ветра в интервале измерения i; n — количество интервалов измерений.
Для численной оценки разброса скоростей ветра от среднего значения используется коэффициент вариации средних скоростей, который определяется выражением [18]:
где Sv — среднеквадратичное отклонение текущей скорости ветра от среднего значения; V ср — средняя скорость ветра за исследуемый период времени.
Известно, что скорость ветра по мере удаления от подстилающей поверхности возрастает и воздушный поток становится более устойчивым. Приближенно скорость ветра на высоте h может быть оценена по формуле
Vh = Vф (h / hф )а,
где Vh — скорость ветра на высоте h; Vф — скорость ветра на высоте флюгера; hф — высота флюгера; а — коэффициент, зависящий от средней скорости ветра на высоте флюгера.
Для открытой местности и небольшой шероховатости подстилающей поверхности принимается а = 1/7. Зависимость значений а от скорости ветра иллюстрируется данными таблицы 5 [6].
Зависимость а от скорости ветра Vф
|
Таблица 5
|
Важный энергетический показатель «Повторяемость различных градаций скорости ветра» можно рассматривать как процент времени, в течение которого наблюдалась та или иная градация скорости ветра. Эта характеристика важна для расчета энергетических и других параметров, необходимых для ветроэнергетических расчетов, связанных с оценкой интервалов времени работы ветроэлектростанции при различных скоростях ветра. В качестве примера распределения ветрового потенциала в течение года по градациям в таблице 6 приведены данные метеостанции Александровское Томской области.
Повторяемость скорости ветра по градациям представляет собой временную характеристику скорости ветра. Кроме эмпирических зависимостей типа данных табл. 6, для описания характеристик скоростей ветра используются некоторые модельные функции, описывающие распределение случайных значений скоростей ветра V в соответствии с выражением F(V) — интегральная функция распределения, равная вероятности того, что скорость ветра больше значения V; f(V) = — dF(V)/dV —
дифференциальная функция распределения, равная плотности вероятности.
Повторяемость (%) различных градаций скорости ветра
|
Таблица 6
|
Среднее значение или математическое ожидание скорости ветра М(У) определяется по выражению
M (V) = j Vf (V )dV.
0
Известны различные типы функций распределения скоростей ветра — Вейбулла, Рэлея, Грищевича и др. [23]. Одной из наиболее распространенных на практике функций, дающей наиболее точные результаты в диапазоне скоростей ветра 4…20 м/с, является распределение Вейбулла, описываемое выражениями:
F (V) = e-(V / c) k;
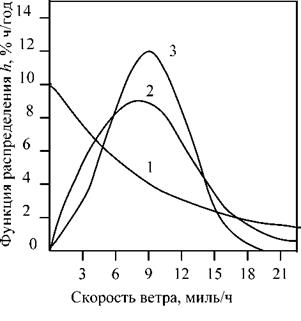
где коэффициент с, имеющий размерность скорости, характеризует масштаб изменения функции распределения по оси скоростей, а коэффициент k характеризует крутизну распределения. Графически функции распределения вероятностей имеют вид, показанный на рис. 2 [23 ].
Функция распределения Вейбулла при k = 1 соответствует экспоненциальному распределению и применяется в основном в теории надежности. При k = 3 распределение Вейбулла приближается к нормаль
ному закону, который часто называется параболическим законом распределения Гаусса.
|
Рис. 2. Функция распределения вероятностей Вейбулла при значении масштабного коэффициента с = 10 и параметров распределения к = 1, 2 и 3 (кривые 1—3 соответственно) |
В качестве интегральной энергетической характеристики ветра широко используется удельная мощность ветрового потока, приходящаяся на единицу площади поперечного сечения потока. Теоретический ветроэнергетический потенциал оценивается с помощью формулы:
Р = 0,5р ср (V 3) Ср,
2
где Р — удельная мощность [Вт/м ]; рср — средняя плотность воздуха
3 3 ^
[кГ/м ]; (V )ср — средний куб скорости.
Средний куб скорости ветра может быть выражен через среднюю скорость как:
(V3) ср = 1,9(^р )3,
а ветроэнергетический потенциал равен
P = 0,95рср (^р )3.
В качестве примера энергетических характеристик ветра на территории Томской области по сезонам года можно привести данные метеостанций, представленные в таблице 7.
Средняя скорость ветра (м/с) и удельная мощность (Вт/м )
для различных сезонов и за год
|
Таблица 7
Примечание: Уф — средняя скорость ветра на высоте флюгера. |
Сезоны, указанные в таблице, не совпадают с календарными, но являются однородными по ветровому режиму [19]: зима (декабрь, январь, февраль), весна (март, апрель, май июнь), лето (июль, август, сентябрь), осень (октябрь, ноябрь).
Максимумы удельной мощности соответствуют переходным сезонам. Основной минимум относится к летнему периоду, а вторичный — к зимнему.
Территориально распределение удельной мощности может характеризоваться двумя зонами: южная часть и пойма реки Оби — здесь Р изменяется в среднем за год в пределах 150…200 Вт/м, а на остальной территории области удельные мощностные показатели не превышают 100 Вт/м2.
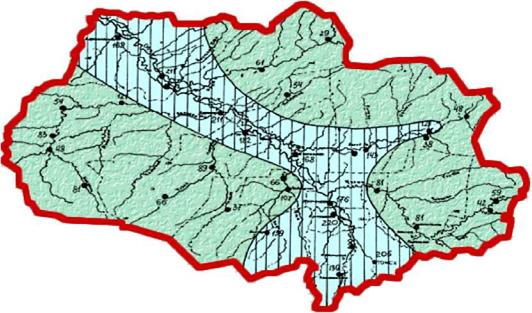
Карта-схема распределения среднегодовой удельной мощности ветра на территории Томской области приведена на рис. 3 [19]. Приведенные характеристики ветроэнергетического потенциала соответствуют высоте флюгера, равной 10 м.
|
2 Рис. 3. Среднегодовая удельная мощность ветра (Вт/м ) |
Для оценки ветрового потенциала территории, в частности валового, может быть использована следующая методика [18]. Валовый потенциал рассчитывается как суммарная энергия системы ветроустановок высотой h, распределенных равномерно по территории на расстояниях, исключающих взаимное влияние энергоустановок. Обычно считается, что возмущенный ветровой поток полностью восстанавливается на расстоянии, равном 20h от ветроэлектростанции. Это условие определяет порядок размещения ветроустановок по территории. Тогда, на территории площадью S (м2) в течение времени Т (обычно год), полная ветровая энергия всех установок определится как
или
![]()
W в = 4: pTS J v3 f (V )dv,
40 0
где V, ti — градации скорости ветра и их относительная продолжительность.
Технический ветровой потенциал территории может быть определен с учетом двух обстоятельств.
Первое — площадь территории, пригодной по хозяйственным и экологическим условиям для размещения ветроэлектростанций. Тогда площадь территории St, пригодной для использования ветровой энергии, равна St = qS, где q — коэффициент, зависящий от конкретного региона.
Фактически St — это часть территории S, остающаяся после вычитания площадей сельхозугодий, промышленных и водохозяйственных территорий, различных строений и пр.
При определении технического потенциала территории в настоящее время рекомендуется придерживаться некоторых правил [19]:
1. Для ветроэлектростанций большой мощности (более 100 кВт) коэффициент использования установленной мощности должен быть не ниже 20 %.
2. Эффективность использования ветровой энергии увеличивается с ростом мощности ветроэнергетических установок (в настоящее время их мощность доходит до 4.. .6 МВт).
3. Обычно для размещения ветроэлектростанций может использоваться не более 30 % территории.
Второе — технический уровень современных ветроэнергетических установок, характеризуемый генерируемой мощностью в зависимости от скорости ветра. Для сетевых ветроэлектростанций обычно используются ветротурбины с горизонтальной осью вращения на высоте башни 50 м. Кроме технических характеристик собственно ветроэлектростанций, необходимо учитывать порядок их размещения по условию максимального использования энергии ветра.
Мощность ветроэлектростанции P(V) с диаметром ветротурбины
п
D определяется выражением P(V) = — D2 PV3 ■ n(V),
8
где n(V) — КПД установки для скорости ветра V.
Среднестатистическое значение мощности определяется как
П n
Pср = ёD2 Р IV3n(V,0 • ti 8 i=1
или в интегральной форме
п ^
P ср = — D 2 Р V 3W) • f (V )dV. 8 0
Для максимального использования ветрового потока рекомендуется размещать ветроэлектростанции рядами перпендикулярными преимущественному направлению ветра на расстоянии 20D друг от друга. Если направление ветра может равновероятно меняться, то ВЭС целесообразно размещать в шахматном порядке между соседними станциями с расстояниями 20D.
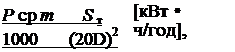 |
|
Тогда, в первом случае на площади 5т можно разместить St/(20D)2 установок, позволяющих получить за год (Т = 8760 ч/год) энергию, равную
или
Wт = ~П{D2РI vjn(Vi) ■ ti ■т Sт 2 [Вт • ч/год].
8000 i=i i (20D)2
Во втором случае можно разместить Sт/(100D2) установок, обеспечивающих технический потенциал энергии ветра территории
W т = ^ • т
1000 100 D 2
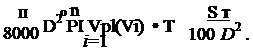 |
|
или, с учетом градаций ветра Vi,
Как следует из приведенных выражений, технический потенциал ветровой энергии не зависит от диаметра и, следовательно, единичной мощности ветроустановок.