Закономерности дискретных процессов
Процессы в реальном микро — и макромире представляют совокупность единичных актов взаимодействия отдельных частиц и тел; то есть реальные процессы – дискретны. В то же время, классическая физика с давних времен рассматривает континуальные (непрерывные) процессы. Исторически это, видимо, вызвано способностью человека ощущать, чувствовать именно такие, недискретные, процессы, в том числе изменение температуры, давления, уровня воды и т. п.
Математический аппарат, в частности, интегро-дифференциальное исчисление, также приспособлен к описанию недискретных процессов, процессов в полях средних (среднестатистических) величин. Это – как средняя температура пациентов в клинике: не учитываются многие дискретные акты взаимодействия, в том числе, определяющие течение процессов, особенно, при фазовых переходах, а также – процессов в микромире. Разработка представлений о механизмах дискретных процессов, зависимостей и алгоритмов для их описания способствует преодолению кризиса современной классической физики.
Такие зависимости представлены в /15/. Основными из них являются:
(1) 
– третий закон Ньютона в форме Ньютона;
(2) 
– динамический закон Кулона;
(3) 
– закономерность динамики фотоэффекта;
(4) 
– закон сохранения количества частиц и эволюции многочастичной системы;
(5) 
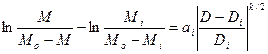– макрозакономерность фазового перехода;
(6) 
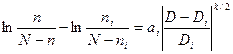– микрозакономерность фазового перехода.
Уравнение (1) встречалось выше. Это – закон сохранения изменения энергии. Он стал известен в России с 1915 года, с момента издания русского перевода труда И. Ньютона «Математические начала натуральной философии» с латинского (1686 год).
Однако им пользовались в форме равенства статических сил 
как результата действия сил, приведшего к напряженному состоянию. По Ньютону закон (1) читается так: произведение силы действия на скорость действия равно произведению силы реакции на скорость реакции. Это может привести к возникновению больших сил (по аналогии с домкратом, полиспастом, рычагом, ударом, взрывом и т. п.) и образованию нового качества, например, высокопотенциальной энергии взамен затраченной низкопотенциальной. То есть, третий закон в форме Ньютона исключает второй закон классической термодинамики об одностороннем изменении энтропии только в сторону ее увеличения.
Применение третьего закона в форме Ньютона обязательно к процессам микромира, которые являются дискретными, так как определяются актами взаимодействия между собой индивидуальных частиц при высоких, околосветовых, скоростях их движения.
Уравнение (2) – это связь причины-действия, как произведения силы на скорость фотона 
, и энергетическим обеспечением – следствием действия в элементарном акте. Здесь: 
– постоянная тонкой структуры; 
– энергия; 
– частота; 
– постоянная Планка как характеристика минимального действия.
Уравнение (3) показывает, что маленькая сила 
действия фотона, движущегося с большой скоростью (света), в веществе с малой скоростью распространения возмущений (скоростью 
звука) вызывает большую силу 
, локализованную в микрозоне и способную привести к возникновению новой структуры, фазы, выделению энергии, в том числе, высокопотенциальной, то есть привести к созидательному процессу, а значит уменьшению энтропии системы.
В уравнении (4) функция 
, называемая Синергией и Лагранжианом, являющаяся аналогом энтропии 
, много больше ее, >>
.
Это свидетельствует о том, что система взаимодействующих частиц несоизмеримо более вероятна, чем идеальная система распределения частиц в модели молекулярного хаоса. Собственно, именно это практически показал Д. Х.Базиев /3/ на примере организованного электродинамического взаимодействия молекул газа, в том числе воздуха, описанном в первой части настоящей монографии.
Все типы фазовых переходов имеют единую закономерность: (5) – для изменения характеристики 
(температура, давление и т. п.); (6) – для изменения числа частиц, так как пропорциональна числу 
прореагировавших частиц. Здесь:
– максимальное значение характеристики;
– характеристика на 
-той стадии процесса;
– внешнее воздействие;
показатель 
– для одномерных процессов, 
– для двумерных и 
– для трехмерных.
Графики (5), (6) имеют вид логистической (гистерезисной) кривой и совпадают, трансформируются в одну кривую, для разных веществ и фазовых переходов.
Приведенные зависимости (1)-(6) приспособлены к описанию дискретных множеств, что наиболее полно отражает течение и динамику реальных процессов в природе.