Бурение грунтовых зондов, установка энергетических колодцев

Длины волн (или полуволн), на которые умножается число фазовых циклов, представляют собой цену фазового цикла в линейной мере, различную для первого и второго каналов системы. Так как длина волны зависит от скорости распростра­нения радиоволн в атмосфере, а скорость зависит от метео­условий, то цена фазового цикла не является строго постоянной величиной. Практически для цен фазовых циклов принимают некоторые средние значения, определенные из предваритель­ных экспериментальных измерений в полевых условиях на участке работ. Определение цен фазовых циклов называется
калибровкой системы. Калибровка обязательна для всех си­стем ДВ и СВ диапазонов, ведущих запись фазовых циклов. При автоматизации измерений в вычислительное устройство изначально вводятся постоянные значения длин волн, соответ­ствующие стандартным условиям атмосферы, а результаты из­мерений исправляются поправками за отличие реальных усло­вий от стандартных.

Необходимость калибровки’ обусловлена также еще одним обстоятельством, связанным с отражениями радиоволн от под­стилающей поверхности. Дело в том, что появление дополни­тельного сдвига фазы из-за отражений от подстилающей по­верхности можно интерпретировать как изменение фазовой скорости радиоволн. В самом деле, закон изменения фазы

‘с расстоянием, обычно записываемый в видеф = со^———— —j

где v = c/n — фазовая скорость радиоволн, для ДВ и СВ диа­пазонов должен быть представлен в виде

<р = ©^—^ — фдоп, (4.72)

где дополнительный сдвиг фдоп зависит от электрических пара­метров подстилающей поверхности, расстояния, частоты излу­чения и высоты подъема радиостанций. Взяв полный дифферен­циал от (4.72) и приравняв его к нулю, получим.

dw = (ndt—(о — дфдап dr _ q (4.73)

v дг ‘

Так как скорость выражается производной dr)dt, то из (4.73) получим, что изменившееся значение фазовой скорости будет

т. е. наличие фдоп эквивалентно уменьшению фазовой скорости v

на ——^Рдоп . Зависимость фдоп от расстояния, выражаемая 2 п дг

производной <?фд0п 1дг, при небольших удалениях от излучаю­щей радиостанции нелинейна и весьма сложна, но на расстоя­ниях в. несколько десятков километров и более она приобре­тает линейный характер, и дфдоп/дг мало изменяется с рас­стоянием. По экспериментальным данным, производная дфдоп /дг, начиная с расстояния примерно 40 км, остается почти постоянной величиной, и это постоянство улучшается с увели­чением частоты. Постоянство дфдоп/дг, как видно из (4.74), обозначает постоянство фазовой скорости на трассе. На этом и основана возможность экспериментального определения цены фазового цикла А, ф=Оф//: мы не можем определить »ф, но если она постоянна в процессе измерений, то, измерив системой
заранее известные величины соответствующих приращений или разностей расстояний, можно получить А, ф, поделив эти изве­стные величины на измеренное число циклов.

Однако такая калибровка не будет отличаться особенно высокой точностью. Даже если дфДОп/дг=const, скорость Уф не может быть постоянной из-за зависимости величины v = c/n от метеоусловий (показателя преломления). Кроме того, сама ве­личина дфдоп/дг никогда не бывает строго постоянной. На ее значение, например, влияет рельеф местности. Невозможность учета всех факторов приводит к тому, что точность систем ДВ и СВ диапазонов не превосходит величины, лежащей в преде­лах от единиц до десятков метров. Более высокая точность обеспечивается системами УКВ диапазона.

Говоря о точности РГС, нужно различать точность измере­ний, выполняемых системой, и точность определения положе­ния пунктов при помощи РГС. Точность измерений — это та точность, с которой получаются измеряемые величины — рас­стояния или разности расстояний. Она определяется, как обычно, аппаратурными ошибками и ошибками из-за неточного учета внешних условий. Точность определения положения пункта — понятие несколько более сложное. Положение пункта определяется координатами, вычисляемыми по измеренным ве­личинам, и поэтому точность координат зависит не только от точности измеренных величин, но и от геометрического поло­жения определяемого пункта относительно базисов системы.

Приведем без вывода выражения для средней квадратиче­ской ошибки положения пункта М= — y/ntx + ntY (<Пх и ту — ошибки координат) для круговых и гиперболических систем (подробный анализ этого вопроса мощцо найти, например, в [1, 8, 11,13]):

для круговых (однобазисных) систем

Мкруг = -!^-; (4.75)

siny

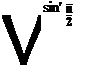для гиперболических (двухбазисных) систем

где mr и Шаг — ошибки измерения расстояния и разности рас­стояний соответственно; у, у и у2 — углы, под которыми видны из определяемого пункта базисы системы (углы за­сечки).

Площадь, в пределах которой ошибка М не превышает за­данной (допустимой) величины, называют рабочей зоной ра- диогеодезичоской системы. Эта площадь ограничена кривой равных ошибок МДОп=const и может иметь различные конфи­гурации.

Комментарии запрещены.