Бурение грунтовых зондов, установка энергетических колодцев

В случае измерения больших расстояний вторым этапом об­работки, как уже отмечалось ранее, является редуцирование на поверхность референц-эллипсоида и на плоскость в проекции Гаусса — Крюгера.

Остановимся вкратце на том общем принципе, который по­ложен в основу редуцирования линейных величин на референц — эллипсоид.

При редуцировании на эллипсоид необходимо получить длину геодезической линии, соответствующей редуцируемому расстоянию. Практически же вполне допустимо отождествить длину геодезической линии, соединяющей две точки на эллип­соиде, с длиной дуги нормального сечения из первой точки на вторую, ибо разность длины этой дуги и геодезической линии ничтожно мала (менее 10_3 мм при расстоянии 600"км).

Далее, для упрощения вывода редукционной формулы заме­няют длину дуги нормального сечения дугой окружности, т. е. заменяют референц-эллипсоид шаром, и получают формулу, в ко­торой фигурирует радиус шара R. В первом приближении R по­лагают равным среднему радиусу Земли (6371 км), что допус­тимо при обработке измерений, выполненных радиогеодезиче­скими системами не очень высокой точности и при не слишком больших расстояниях. При желании получить более точный ре­зультат в качестве R используют средний радиус кривизны эл­липсоида R3=V MN для средней точки линии (М — радиус кри­визны меридиана; N — радиус кривизны первого вертикала в этой точке). Наконец, при еще более точных вычислениях (ре­дуцирование результатов измерений свето — и радиодальноме­рами) в качестве R принимают радиус кривизны нормального сечения, проходящего через одну из конечных точек или, лучше, через среднюю точку линии (точку со средней широтой). Ра­диус кривизны нормального сечения Rn может быть вычислен, если известны азимут линии и ее средняя широта (соответ­ствующие формулы выводятся в курсе сфероидической геодезии и будут приведены ниже).

Итак, редукционная задача сводится к вычислению длины дуги окружности, в качестве радиуса которой затем подставля-

ется в зависимости от требуемой точности средний радиус сфе­рической Земли, средний радиус кривизны эллипсоида или ра­диус кривизны нормального сечения. Длину дуги окружности проще всего получить, вычислив сначала длину хорды, стяги­вающей эту дугу, и затем введя в результат соответствующую поправку, подобно тому, как это делается при рассмотрении ре­фракционного удлинения траектории, принимаемой за дугу ок­ружности (см. § 10, рис. 19).

Для вычисления длины хорды по измеренной наклонной дальности требуется, как мы увидим далее, знать геодезические высоты Н конечных точек линии, т. е. высоты их над референц- эллипсоидом. В каталогах же высот и на картах всегда приво­дятся не геодезические, а нормальные высоты Ну, эквивалент­ные высотам точек линии над квазигеоидом. При невысокой точности радиогеодезических измерений в отдельных случаях можно пользоваться нормальными высотами вместо геодезиче­ских, но при точных измерениях нужно получить геодезические высоты, связанные с нормальными высотами, как известно, со­отношением #=#v+£, где величина £ (аномалия высоты) есть превышение квазигеоида над референц-эллипсоидом. Эта величина может быть найдена при помощи специальных таблиц или по карте высот квазигеоида (геоида) над референц-эллип­соидом.

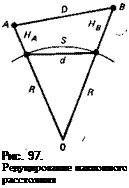
Общая формула для редуцирования линии. Получим общую формулу для редуцирования наклонного расстояния на сферу радиуса R. На рис. 97 AB=D — редуцируемое расстояние; точки а и b — проекции точек Л и В на сферу; НА и Нв — геодезиче­ские высоты точек А и В; d — хорда; S — дуга окружности, длину которой требуется получить. Из треугольника aob имеем

d? = Ri + R2—2#acosy = 2#a(l—cosy), (5.18)

а из треугольника АО В

D2 = (R + На?+(R + Нв?—2 (R + НА) (R + Нв) cos у. (5.19)

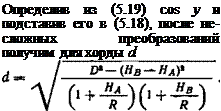(5.20)

Переход от длины хорды d к длине дуги S осуществляется по формуле (см. § 10)

(5.21)

В последнем члене этой формулы в любых случаях допустимо вместо d брать значение измеренной дальности Дав качестве

R— средний радиус земного шара R0, и окончательная общая формула редукции может быть записана в виде

S = d+-¥~, (5.22)

24*15

где d определяется формулой (5.20).

Радиус кривизны нормального сече­ния Rn, используемый в качестве R в (5.20) при наиболее точном приближе­нии, вычисляется по формуле:

Rn = Rs(l — — y cos 2Bm • cos 2A ); (5.23)

здесь Вт — средняя широта линии; А — азимут; Ra — средний радиус кривизны Вт, равный

где а — большая полуось эллипсоида; е — его первый эксцен­триситет. Для референц-эллипсоида Красовского а=6378245 м; е2=0,0066934216. Значения R3 и Rn для диапазона широт 36— 79° приведены в прил. 2 и 3.

Ошибка от замены длины дуги нормального сечения дугой окружности радиуса Rn, как показывают расчеты, может счи­таться пренебрегаемой вплоть до расстояний 600 км.

Лишь при измерении расстояний более 600 км следует вычис­лять не длину окружности радиуса Rn, а непосредственно длину дуги нормального сечения или геодезической линии на поверх­ности эллипсоида. Практически такое вычисление можно осу­ществить, перейдя от хорды окружности радиуса Rn, т. е. от ве­личины d, определяемой формулой (5.20), к хорде нормального сечения эллипсоида d3 и далее к длине геодезической линии S3 на эллипсоиде по формулам:

d3 = d—^/cos2BmcosM(tfm————— ); (5.25)

S3 = d3 + (1 + /- cos2 Вт• cos2 А)2, (5.26)

24 7va

где N =———————— радиус кривизны первого вертикала

(1 — е* sin* Вт)112

для средней широты Вт е’ — второй эксцентриситет [е’ = = 0,0067385254); Ят = — у — (На + Нв) — средняя высота линии. Величины N даны в прил. 4.

Рабочие формулы редуцирования. Выражение (5.20) явля­ется универсальным — оно пригодно для использования как в случае свето — и радиодальномеров, так и при измерениях ра­диогеодезическими системами. На практике его обычно преоб­разуют, внося при этом некоторые допустимые упрощения, и получают результат в виде суммы нескольких членов (поправок к измеренной дальности) достаточно простого вида. Преобразо­вания заключаются в том, что формулу (5.20) записывают в виде

а=о [і — ‘w ]’д (і + 1,2 (і + 1,2

(5.27)

и затем каждый из сомножителей раскладывают в степенной ряд, удерживая определенное количество членов разложения; перемножают ряды и в полученном результате также отбрасы­вают несущественные члены. В итоге получают рабочие фор­мулы, которые могут в различных случаях (измерения свето — и радиодальномерами, измерения разными типами радиогеодези­ческих систем) несколько отличаться друг от друга. Наиболее употребительны следующие формулы (приводим их с учетом со­отношения (5.22), т. е. для длины дуги окружности на сфере относимости):

1) для свето — и радиодальномеров

В этих формулах h=HB—#а.

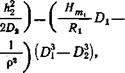Как видим, эти формулы отличаются друг от друга тем, что в (5.28) не учитываются члены ft4/8D3 и H2mD/R2 и добавляется поправка за рефракционное удлинение траектории (последний член), существенная при расстояниях более 150—200 км (р — радиус кривизны траектории радиоволны). Если радиогеодези­ческой системой измеряются не расстояния D, а разности рас­стояний Di—£>2 (гиперболические РГС), то для редуцирования разности расстояний формула (5.29) преобразуется в «разност­ную» формулу

где все индексы 1 и 2 относятся к расстояниям Dx и D2 соответ­ственно. Гиперболические системы определяют две разности рас­стояний (см. рис. 88), и соответственно формула вида (5.30) ис­пользуется дважды. При этом, как видно из (5.30), для вычис­ления поправочных членов нужно знать не разности расстояний, а сами расстояния, которые не измеряются. Однако их доста­точно знать приближенно, и их находят следующим образом: по измеренным разностям расстояний определяют приближенные координаты определяемого пункта при помощи гиперболиче­ской сетки, нанесенной, наряду с сеткой прямоугольных коорди­нат, на планшет участка работ (на котором отмечено положение базисных станций), а затем по полученным приближенным ко­ординатам определяемого пункта и известным координатам ба­зисных станций определяют (решая обратную геодезическую за­дачу) приближенные значения самих расстояний, которые и подставляют в формулы вида (5.30).

В заключение оценим точность, с которой требуется знать среднюю высоту Нт и превышение /і=Яб—На. Запишем от­дельно поправки, содержащие эти величины; при этом доста­точно ограничиться главными членами этих поправок, т. е. рас­смотреть формулу (5.29). Имеем

ДО».| —х°- ‘

Дифференцируя эти равенства соответственно по Л и Нт и пе­реходя к ошибкам, получим

mADh = M1=—mll;

ял D

тАОнт ft ‘

откуда допустимые значения ошибок тн и тНт будут

м,

D ’

Da /

5-Ю-7 —. Как видим, допустимая ошибка определения превы — h

шения тем больше, чем длиннее линия и чем меньше само пре­вышение. При D=30 км и Л=300 м она составляет 1,5 м, а при £>=10 км и том же превышении между пунктами уменьшается до —0,2 м.

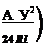Редуцирование на плоскость в проекции Гаусса—Крюгера. При необходимости обработки измерений на плоскости в про­екции Гаусса—Крюгера переход от длины линии 5, редуцирован­ной на эллипсоид, к длине SnjI на плоскости осуществляется по формуле, известной из курса высшей геодезии

где ут= -^-(Ул+Ув) — средняя ордината линии; Ау=Ув—Ул —

разность ординат конечных точек. Если линия расположена не более чем в 150 км от осевого меридиана шестиградусной зоны, второй член в скобке можно не учитывать.

Примеры редуцирования линии. Рассмотрим примеры вычис­ления редукционных поправок для случаев: 1) свето — и радио — дальномерных измерений и 2) радиогеодезических систем.

1. Пусть значение расстояния с учетом постоянной поправки, метеопоправок и поправок за центрировку и редукцию равно 0=26528,356 м; геодезические высоты центров знаков #і =

=218,7 м; Hz=238,4 м; высоты приборов над центрами h = = 1,5 м; Л2=20,8 м; Вт=54,50; Л=22°; t/j = 64,95 км; г/2 = = 74,32 км. Вычисления осуществляются по формуле (5.28), в которой R=Rn выбирается из таблицы прил. 3. При редуци­ровании на плоскость в формуле (5.31) можно брать как R3, так и Rn.

2. Пусть значение расстояния, измеренного круговой РГС, с учетом аппаратурных поправок и поправок за скорость рас­пространения, равно Z?=316,5824 км; геодезические высоты станций (антенн) НА=265,6 м; Яв = 584,8 м; Вт=52,0°; Л = 64°; і/і = 6,96 км; ^2=294,41 км. Вычисления осуществляются по фор­муле (5.29). Радиус кривизны траектории вычисляется как ве­личина, обратная градиенту индекса преломления (см. § 10). В данном примере примем р=25 000 км. Редуцирование на плос­кость осуществляется, как и в первом случае, по формуле (5.31).

Результаты вычислений для обоих случаев представлены в табл. 12.

Комментарии запрещены.