Бурение грунтовых зондов, установка энергетических колодцев

При измерениях радиогеодезическими системами конечной целью является получение координат определяемой точки по известным координатам базисных станций и двум измеренным расстояниям или разностям расстояний. Эта задача, как и урав­нивание сетей, в зависимости от длин линий, необходимой точ­ности и других требований может решаться как в системе прост­ранственных координат, так и на различных поверхностях отно­симости— на сфере, эллипсоиде или плоскости. Так, например, при длинах измеряемых расстояний более 500 км обработку ча­сто выполняют на эллипсоиде в системе географических коор­динат. При использовании любой поверхности относимости измеренные наклонные расстояния путем введения соответ­ствующих поправок приводятся на эту поверхность. Обработка измерений на эллипсоиде и на сфере изучается в соответствую­щих разделах курса высшей геодезии.

Здесь мы рассмотрим наиболее простой случай — решение указанной задачи на плоскости.

Определение координат из измерений круговыми системами. При измерениях круговыми системами получают (см. § 21) два расстояния от базисных станций до определяемой точки и реду­цируют их на плоскость. Заметим, что в этом случае можно оп­ределить местоположение точки простым графическим построе­нием на карте, на которую заранее нанесены базисные станции по известным координатам, однако точность этого способа не­велика, и в большинстве случаев используют аналитический способ вычисления координат определяемой точки.

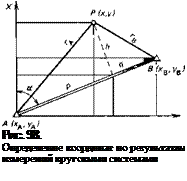
Итак, необходимо определить прямоугольные координаты х и у точки Р(х, у) по известным координатам базисных станций

А{ха, Уа) и В(хв, ув) и измеренным расстояниям гра и ^.ре­дуцированным на плоскость, например, в проекции Гаусса— Крюгера. Обозначим редуцированные расстояния через га и гь, а длину базиса АВ — через d и обратимся к рис. 98, чтобы по­лучить необходимые соотношения на плоскости. Непосред­ственно из чертежа следует:

x = Jc^ + P-cosa-f Л-sin a; (5.32)

У = Уа + Р sin a—A cos a, (5.33)

или

x = xB—</cosa +Asina; (5*34)

У = Ув~Ч-sina—Acosa. (5.35)

Таким образом, координаты точки Р можно вычислить, зная вспомогательные величины р, q и А. Эти величины легко нахо­дятся ПО полученным ИЗ измерений Га И Гь и известной длине ба­зиса d. В. самом деле, из рис. 98 имеем:

А2 = г|—р2 — г—q*; (5.36)

q = d—р; (5.37)

? = <Р—2dp + p (5.38)

Подставляя (5.38) в (5.36), найдем

(5.39)

Аналогичным образом, используя равенство p = d—q, воз­водя его в квадрат и подставляя в (5.36), получим

rl-rl+d2

2d

Для величины А из (5.36) имеем

h = ±л/г1~ Р* = ±л/г1~Я2 ■

Знак «плюс» перед корнем соответствует случаю, когда от­резок направлен вверх от линии АВ, знак «минус» — случаю, когда этот отрезок направлен вниз от линии АВ.

На практике рассмотренные вычисления, как правило, вы­полняются на ЭВМ, которая, в частности, может входить в со­став бортовой аппаратуры РГС.

Определение прямоугольных координат из измерений гипер­болическими системами (задача, фазового зонда). При измере­ниях гиперболическими системами получают (см. § 21) две раз­ности расстояний от трех базисных станций до определяемой точки, называемые гиперболическими координатами. Переход от полученных из измерений гиперболических координат к коорди­натам какой-либо общепринятой координатной системы осущест-

вляется путем решения задачи, часто называемой задачей фазо­вого зонда. Она формулируется следующим образом: найти коор­динаты определяемой точки по известным координатам трех ба­зисных станций и двум измеренным разностям расстояний.

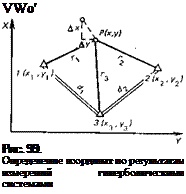
Рассмотрим эту задачу на плоскости, предположив, что из­меренные разности расстояний приведены на плоскость. На рис. 99 представлена соответствующая геометрия на плоскости в системе прямоугольных координат х, у. На этом рисунке для большего удобства при дальнейшем изложении буквенные обо­значения, фигурировавшие на рис. 98, заменены цифровыми: бо­ковые станции В и С обозначены номерами 1 и 2, а централь­ная станция А — номером 3, и все расстояния имеют соответ­ствующие цифровые индексы. Длины базисов обозначим через d и d.2. Редуцированные на плоскость разности расстояний

Аг81=г3—гі; (5.42)

Агз2 = Гз—/j. (5.43)

Выражая расстояния гь г2 и г8 через координаты соответ­ствующих точек, запишем (5.42) и (5.43) в виде

Arsl = V(х—xsy+(у—УаУ —V(x—Xi)2+(у—уїТ ; (5.44)

Аги = V (x—xsy + (у—Уз)2 —У(х—хг)2 + {у— y2f. (5.45)

Мы получили систему двух уравнений с двумя неизвестными х и у, решение которой и дает искомый результат. Однако стро­гое решение этой системы уравнений приводит к громоздким и неудобным формулам. Поэтому решение выполняют способом последовательных приближений (итераций). Искомые коорди­наты х и у точки Р представляют в виде

х = х0+Ддс; (5-46)

У = Уо + &У, (5-47)

где Хо, у0 — приближенные координаты точки Р, и тогда задача сводится к нахождению поправок Ах и А у.

Поправки Ал: й Ay вычисляют по формулам, которые мы при ведем здесь без вывода:

п2Ьгх — ПЬг2 в >	(5.48)
ТПТ12 — /Л2Лі
— Ш2ЬГ “1" ШЬг2 ~ 9	(5.49)

Л У-

гпіп2 — т%пх

где

6/1 = (^8 Гі) ‘(Гоз Гoi)j fir2 = (г3— г,)— (г03 — Г02);
‘-01= V(x0—*і)2 + («/0—Ух? Ли = l^(x0—х*)г + {Уо—УгУ
Ли = V{xo—xsf+{yo—y3Y;

тх =	$ і X со	Xo — Xi	и. —	Уо — Уь	Уо — Уі.
гоз	4 » Г01	‘*1	/оз	* Г01
т2 =	*0 — *3	*0 —*2 .	Пл —	_ Уо — Уо	Уо — У%
г03	Г02 *	■■	Гоз	Гог

Число приближений зависит от точности приближенных ко­ординат х0 и уо — Последним приближением считается такое, при котором поправки Ах и А у оказываются меньше величины, ха­рактеризующей точность данной радиогеодезической системы. Обычно на практике приходится делать от одного до трех при­ближений.

Приближенные координаты можно снять с карты или схемы района работ, построив на ней гиперболическую сетку; при на­личии такой сетки приближенные прямоугольные координаты х0 и уо находят графически по гиперболическим координатам — измеренным значениям разностей расстояний. Построить сетку можно несколькими графическими и аналитическими спосо­бами, однако это довольно кропотливая работа, отнимающая много времени. Применение ЭВМ для решения задачи фазового зонда позволяет обойтись без построения гиперболических се­ток. В этом случае по координатам нескольких точек в районе работ последовательно определяются координаты всех осталь­ных точек.

Комментарии запрещены.