ГЕОМЕТРИЧНИЙ МЕТОД
ГЕОМЕТРИЧНИЙ МЕТОД
Суть геометричного методу вимірювання скручування може бути представлена схемою (рис. 5.2) і реалізована за допомогою вимірювального ФАК та перетворюючого елемента в склад якого входить оптичний клин з невеликим заломлюючим кутом р і кутовий відбивач [154]. Інколи цей метод називається ще двопроменевим.
|
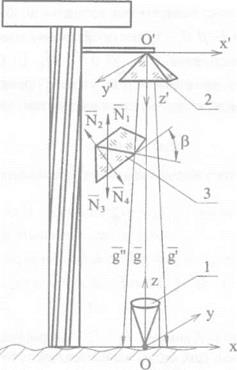
Рис. 5.2. Схема геометричного двопроменевого методу вимірювання кута скручування |
Фотоелектричний автоколіматор, який формує паралельний пучок променів, розташовується на стабільній основі споруди, скручування якої необхідно вимірювати. Таким чином, ФАК пов’язаний з нерухомою системою координат OXYZ. Оптична вісь ФАК сполучується (або розташовується колінеарно) з тією віссю системи координат, скручування навкруги якої необхідно вимірювати, тобто оптична вісь авто коліматора орієнтується уздовж вертикальної осі споруди. На монтажному рівні, скручування якого безпосередньо вимірюється, розташовується кутовий призмовий відбивач 2. Після установлення оптичного зв’язку з автоколіматором, відбивач жорстко скріплюється з елементом конструкції. Відбивач має двогранні кути між відбиваючими гранями, які повертають відбитий пучок променів в напряму протилежному до напряму падаючих променів. В якості відбивача може бути використаний і більш складний дзеркально-лінзовий відбивач. Перед відбивачем 2 розташовується оптичний клин З так, що його грань перекриває (віньєтирує) половину робочої апертури відбивача.
Таким чином, половина паралельного пучка променів до попадання на відбивач 2 проходить через оптичний клин-3 , а друга половина — не проходить. При цьому промені, які падають на відбивач і не пройшли оптичний клин не змінюють свого напряму. Промені, що попадають на відбивач, але попередньо пройшли через оптичний клин, відхиляються на деякий кут а, який визначається заломлюючими якостями клина. Після відбиття від
відбивача промені, які пройшли через оптичний клин, змінюють свій напрям на 180°, зміщуючись упоперек осі OZ на половину значення апертури відбивача в бік вільний від віньєтирування оптичним клином. Повертаючись в фокальну площину ФАК ці промені бу
дують перше зображення марки по одну сторону оптичної осі. Промені, які не пройшли через клин, після відбиття від відбивача змінять свій напрям на 180° і лінійно перемістяться упоперек осі OZ на половину значення апертури в бік віньєтирування клином.
Попадаючи на оптичний клинок, останній відхилить промені на кут а, після чого промені побудують в фокальній площині автоколіматора друге зображення марки. Це зображення буде симетричне першому відносно осі, яка задає вісь падаючого пучка.
Розташуємо оптичний клин відносно осей системи координат O’X’Y.’Z’ так, що нормаль N1 до першої заломлюючої поверхні має координати {0,0,-1}, а нормаль до другої поверхні Л/2 має координати {- р, 0, -1} при проходженні клина променем в зворотньому напрямі (після відбиття від відбивача) і N3 [0,0,1}, N4 [р, 0,1} при проходженні клина променем в прямому напрямі на відбивач. Тоді напрям променя q’ після відбиття відбивачем і проходження оптичного клина в нерухомій системі координат OXYZ можна визначити за формулою:
q’ = Т2Т^, (5.1)
а напрям променя q", відбитого відбивачем після заломлення оптичним клином буде визначатись за формулою:
q’^TJ’q, (5.2)
 (5.3)
(5.3)
матриці заломлюючого оптичного клину для двох напрямів променів. Для малих заломлюючих кутів клина матриця заломлення Т2 має вигляд [74]:
|
( 1 |
-X/jPz |
wPz |
||
|
То iyPz |
1 |
-л |
s |
(5.4) |
|
-vPy |
шРх |
1 |
||
|
/-» / w / ? у/ ^ /»4 / і •+■ 1 # 1 |
-1)/(qN)2 -1; |
(5.5) |
п — показник заломлення матеріалу клина;
Рх, Р,, Pz — компоненти вектора, направленого уздовж ребра еквівалентного клина; N — нормаль до вихідної грані оптичного клина.
Для матриці Т2 вектор Р = —[л//Л/2]/р, а для матриці Т2 вектор Р = -N4N3/ р. Вектори Р, Л//, Л/2, Л/3, N’4 визначені відносно осей координат O’X’Y.’Z’ .тобто в рухомій системі координат, а необхідно вектори Л/г’, Л/2, N3, N4 задати в нерухомій системі
OXYZ. Перехід від системи координатО’Х’У7′ до системи координат OXYZ здійснюється за допомогою матриці обертання, елементи якої виражаються через три незалежні кути повороту <р2, q>3 (кути Ейлера) [9]
 |
 |
де / = 1,2,3,4.
Після підстановки матриць 7) і Т2 в (5.1) і (5.2), з урахуванням (5.6) і q = ,0,-і}, координати X і Y векторів q’ і q" відбитих пучків будуть мати вигляд:
X’ = — X” = — у/ cos ft cos ср3,
У = — У = Ч* cos ср2 sin ср3. ^5’7^
Аналіз виразів (5.7) показує, що якщо кути ft і ср2 дорівнюють нулю, то кут повороту відбитих пучків однозначно визначає кут скручування ср3.
Крім того, можливо визначення кута скручування (р3 при наявності кутів розкручування ft і q>2. В цьому випадку виникає відносна похибка визначення кута ср3, яка може
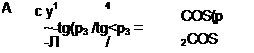 |
|
бути визначена за формулою:
Як видно із (5.8) похибка А не залежить від значення кута скручування ср3, а визначається тільки кутами ft <р2. Відомо, що при використанні в якості перетворюючого елемента оптичного клина в поєднанні з кутовим відбивачем, така конструкція забезпечує високу точність вимірювання скручування навіть при наявності розкручування об’єкта на кути ft і ср2. Наприклад, в діапазоні кутів ft і ср2 рівними ± 6° похибка А не перевищує ±0.6%.