Бурение грунтовых зондов, установка энергетических колодцев

Фазовое детектирование на частоте модуляции может осу­ществляться либо в устройстве, аналогичном модулятору света, либо в фотоприемнике. В первом случае схема имеет, как пра­вило, «симметричное» построение и часто называется схемой с синхронной демодуляцией.

Схема с синхронной демодуляцией в устройстве, аналогич­ном модулятору света. Такая схема в принципе была применена еще в 1928 г. Каролюсом и Миттельштедтом для определения скорости света и затем была положена в основу широко рас­пространенного в свое время советского визуального светодаль­номера СВВ-1, послужившего прототипом для всех разработан­ных позднее визуальных светодальномеров (дальномеры серий СТ, ТД, «Кристалл»). В настоящее время дальномеры с син­хронной демодуляцией имеют фотоэлектрический приемник света. В качестве примера можно назвать дальномеры СГ-3, ДВСД-1200 (СССР), Мекометр ME 3000 (Швейцария). .

Обобщенная блок-схема рассматриваемого варианта соот­ветствует рис. 45. Основным в этой схеме является то, что мо­дулирующее напряжение от генератора синхронно подается на модулятор света и на фазовый детектор (демодулятор), в ка­честве которого используется точно такое же устройство, как и модулятор. Если дальномер имеет плавное изменение частоты генератора (в частности, все визуальные дальномеры), то в схему вводится частотомер (показан на рис. 45 пунктиром). Если же дальномер работает на фиксированных частотах, то вместо частотомера обычно вводится оптическая линия за­держки (ОЛЗ) переменной длины (причем она может быть введена либо в приемный, либо в передающий тракт — в прин-

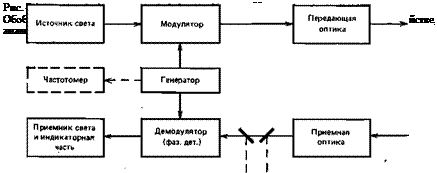ципе это не имеет значения; на рис. 45 ОЛЗ показана в прием­ном тракте). Оптической линии короткого замыкания (ОКЗ) не требуется. Индикаторная часть схемы может строиться раз­личным образом, ее устройство здесь несущественно. (В про­стейшем случае, когда дальномер — визуальный, приемником света и одновременно индикатором является просто глаз наблю­дателя.) Наконец, возможны модификации рассматриваемой схемы, в которых модуляция и фазовое детектирование происхо­дят в одном и том же устройстве, служащем модулятором при передаче и демодулятором при приеме; при этом передающая и приемная оптические системы также совмещены. Эти техниче­ские варианты построения схемы не меняют ее существа с точки зрения принципа работы. .

В схеме с синхронной демодуляцией, как правило, модуля­тором и демодулятором служат электрооптические устройства — ячейки Керра или ячейки Поккельса. Рассмотрим теорию ра­боты схемы в наиболее общем виде, справедливом при исполь­зовании любого из указанных электрооптических устройств, а также независимо от того, какая применена регистрация све­та— визуальная или фотоэлектрическая.

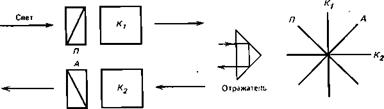
Обычно используется такое взаимное расположение электро — рптических ячеек, которое позволяет реализовать так называе­мый компенсационный способ экстремума (КСЭ). Передающая ячейка (модулятор) состоит (рис. 46, а) из поляризатора Я и электрооптического элемента Ki[14], а приемная ячейка (демоду­лятор) — из электрооптического элемента Кг и анализатора А. Электрооптические элементы Ki и Кг — это либо конденсаторы

Демодулятор Рис. 46. Расположение элементов электрооптических ячеек (а) и направление осей пропускания поляроидов и электрических полей электрооптических элемен­тов (б)

Керра с нитробензолом, либо электрооптические кристаллы (на­пример, типа KDP); поляризатор и анализатор — это совершенно одинаковые поляризационные призмы (типа призмы Николя) или, гораздо чаще, пленочные поляроиды. Поляроиды и элект­рооптические элементы устанавливаются так, что оси пропуска­ния поляроидов П и А (т. е. направления, в которых они линейно поляризуют свет) взаимно перпендикулярны, а направления оп­тических полей в /Сі и /С2 также взаимно перпендикулярны, но образуют с осями пропускания поляроидов углы 45° (рис.46,б).

Нетрудно видеть, что такая система из двух поляроидов и двух электрооптических элементов отличается от амплитудного модулятора света (см. § 12, рис. 34) только наличием вто­рого электрооптического элемента, удаленного от первого на расстояние 2D и развернутого относительно него на 90°. Для амплитудного электрооптического модулятора интенсивность выходящего излучения определяется общим соотношением (см., например, формулу (3.7)

/ = /0 sin2 — у-, (3.22)

где /0 — интенсивность линейно поляризованного излучения, вхо­дящего в электрооптический элемент; ф — разность фаз двух ортогонально поляризованных составляющих на выходе элект­рооптического элемента. Эта разность фаз зависит от приложен­ного напряжения и равна я —- f — const’ при эффекте Пок-

^Х’2

/ и г

кельса и я|———— 1 при эффекте Керра (С/х/г — полуволно-

V UX!2 )

вое напряжение, см. § 12), так что в обобщенной записи ее можно представить функцией ф(С/п), где п равно 1 или 2 и, следовательно, формулу (3.22) переписать в виде ’

7 = /0 sin2 ф ((/")]. (3.23)

Как изменится эта формула при введении в амплитудный модулятор второго электрооптического элемента, развернутого на 90°? Изменение направления электрического поля на 90° во втором элементе по отношению к первому приведет к тому, что та из ортогонально поляризованных составляющих, которая в первом элементе распространялась с большей скоростью и, следовательно, опережала по фазе другую составляющую, во втором элементе будет распространяться с меньшей скоростью и отставать по фазе от другой составляющей, и наоборот. Вслед­ствие этого разность фаз между составляющими ф2, приобретен­ная во втором элементе, будет противоположна по знаку раз­ности фаз фь приобретенной в первом элементе. Оба электрооп­тических элемента можно представить одним эквивалентным элементом со сдвигом фаз между составляющими ф, равным алгебраической сумме сдвигов фаз в обоих элементах. Поэтому в нашем случае

/ = /0sin2^|-_^-) = l0si4±p{U^-^[m)l (3.24)

К обоим электрооптическим элементам прикладывается на­пряжение от одного и того же генератора. Пусть это напряже­ние имеет вид U(t) = U0 + Umsin(iit. Однако необходимо учесть, что свет попадает во второй электрооптический элемент через промежуток времени x2d=2DIv после выхода из первого эле­мента. Этот сдвиг по времени эквивалентен (с точки зрения влияния на конечный результат) сдвигу фазы <р2с=ют2о напря­жения, поступающего на второй элемент, т. е. можно записать: U = U§— Uт sin at, U2 = U0—Umsin.((at — ф2d), и тогда (3.24) приобретает вид

• Щ = /0 sin* -L (ф (U0 + Um sin at)n —

—ф[^0 +^mSin(©/ —фго)]"}. (3.25)

Таким образом, световой поток, прошедший через всю си­стему и поступающий на приемник, описывается выражением (3.25). Этот поток, как мы видим, изменяется во времени с ча­стотой модуляции о. Инерционный индикатор дальномера, по­стоянная времени которого значительно больше периода моду­ляции, реагирует на среднее за период Т=2л/а значение саєто­вого потока, т. е. на величину _ т т

1 = ■-у — /о (0 dt = 5 {sin2 — L {ф (t/0 + um sin Ы)п-

■ 0 0

—ф [{U0+Umsin (at — фго)]"}) dt. (3.26)

Из (3.26) видно, что зависимость I от ф2о весьма сложна, но при этом имеет место одно характерное обстоятельство: если ф2в=2яМ, где N=0, 1, 2, …, то 1=0. Следовательно, если кэ — ким-то образом плавно изменять <p2d и следить при этом за интенсивностью света, то в момент нулевой интенсивности иско­мая разность фаз <ргd окажется приведенной к значению 2nN.

Техническое осуществление этой процедуры зависит от того, какой мы имеем дальномер — с переменной частотой модуляции или с фиксированными частотами.

В дальномере с переменной частотой требуемое соотношение ф2л=2яЛ^ (это соотношение часто называют целочисленным ус­ловием) устанавливается изменением частоты модуляции f. Так как всегда (p2D=2nfr2D и T2d=2D/v, то целочисленное усло­вие записывается в виде

2nf — = 2nN, . (3.27)

V

откуда

D= — N = — N. (3.28)

Ч 2

В дальномере с фиксированными частотами соотношение ф2в = 2nN достигается изменением самой величины <ргс посред­ством изменения пути света в оптической линии задержки [15]. Если считать, что при этом <рго изменяется на Д<р, получим ра­венство

2л/ + Дт = 2nN, (3.29)

V

откуда

D=-2-N + l={±N + l, (3.30)

Щ 2

где /=————- ——- сдвиг Дф, выраженный в линейной мере

21 2л

и определяемый отсчетом по OJI3.

Таким образом, измерив либо частоту модуляции /, либо из­менение фазы в линейной мере /, при которых наступает нулевая интенсивность света на выходе демодулятора, можно вычис­лить расстояние D; при этом для определения целого числа N такие измерения должны быть выполнены как минимум на двух различных частотах в дальномере с переменной частотой и на двух или более фиксированных частотах в дальномере вто­рого типа (см. § 4).

На практике из-за неизбежного различия параметров моду­лятора и демодулятора и неточной их установки получается не нулевая, а некоторая минимальная интенсивность света при це­лочисленном условии.

Компенсационный способ экстремума, описанный выше, отно­сится к так называемым экстремальным способам измерений,
при которых фиксируется мини­мум или максимум сигнала.

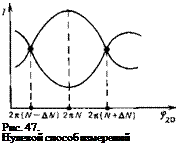В схеме рассмотренного типа может быть также использован компенсационный нулевой (рав­носигнальный) способ измере­ний, который часто называют способом сравнения. При этом способе после демодулятора об­разуются два световых сигнала, создаваемых обычно поляриза­ционными методами (например, расщеплением на два световых пучка с ортогональными поляризациями при помощи установ­ленной после демодулятора двулучепреломляющей пластинки). Интенсивность этих сигналов при изменении частоты или рас­стояния, т. е. при изменении измеряемой разности фаз ф2d, из­меняется в противофазе (рис. 47). При ф2в=2яЛ/ интенсивность одного из сигналов минимальна, а другого — максимальна; если разность фаз сдвигается от значения 2nN, интенсивность одного из сигналов будет возрастать, а другого — убывать, и при неко­тором значении разности фаз интенсивности обоих сигналов ста­нут равными. Из рис. 47 видно, что это происходит в точках, симметричных относительно значения 2nN на фазовой оси; в од­ной из них разность фаз будет 2n(N—AN), а в другой 2n(N+ +AN). Поэтому, если фиксировать две эти точки, т. е. изменять частоту (в дальномерах с переменной частотой модуляции) или фазу (в дальномерах с фиксированными частотами) до момента равенства интенсивностей сигналов последовательно в двух смежных точках, то среднее из отсчетов частоты или длины ОЛЗ в двух этих точках будет соответствовать целочисленному условию (f=2nN. Такой способ называется нулевым, поскольку фиксируются точки, в которых разность интенсивностей двух противофазных сигналов равна нулю. Нулевой способ повы­шает точность фиксации разности фаз в 2—3 раза по сравне­нию с компенсационным способом экстремума.

Схема с фазовым детектированием в фотоумножителе на ча­стоте модуляции используется значительно реже, чем схема с синхронным фазовым детектированием в оптическом демоду­ляторе. Она применялась главным образом в фотоэлектриче­ских дальномерах прежних выпусков — в дальномере ЭОД-1 (СССР), в геодиметрах первых моделей (Швеция), хотя иногда кладется в основу построения и более поздних приборов (совет­ский дальномер МСД-1М). Модулирующее напряжение от гене­ратора подается на модулятор света [16] и на фотоумножитель,

который здесь является одновременно приемником света и фазо­вым детектором. В этой схеме, так же как и в схеме с опти­ческим демодулятором, может использоваться как плавное из­менение частоты генератора, так и фиксированные частоты; в первом случае необходим частотомер, а во втором случае, бо­лее распространенном, опорное напряжение обычно подается на ФЭУ через фазовращатель. (Заметим, что с принципиальной точки зрения при фиксированных частотах роль фазовращателя может играть ОЛЗ.) Опорное напряжение выгодно приклады­вать к ФЭУ при помощи внешнего электрода — диска с отвер­стием или проводящего слоя, напыленного на торец баллона ФЭУ со стороны фотокатода, так что фазовое детектирование происходит в прикатодном пространстве фотоумножителя, т. е. до того, как свет выбивает из катода фотоэлектроны, и поэтому ‘время их пролета не входит в выражение для продетектирован­ного сигнала. Это выражение для среднего за период модуля­ции значения тока на выходе ФЭУ имеет вид

/ = А + В cos (dt2d> (3.31)

где А и В — постоянные (для конкретного случая) величины.

Сигнал вида (3.31) подается на индикаторное устройство, ко­торое для повышения точности обычно строится по схеме ампли­тудного синхронного детектирования, с применением фазовой манипуляции (периодической переброски фазы сигнала в опор- лом или сигнальном канале на 180°). При этом ток / на выходе ФЭУ периодически меняет свою величину с низкой частотой пе­реброски фазы (десятки герц), т. е. становится пульсирующим, и амплитуда пульсации зависит от разности фаз в опорном и сигнальном каналах. Изменяя эту разность фаз фазовращате­лем, можно добиться прекращения пульсаций, что обнаружива­ется по нулевому показанию индикатора. В этот момент будет справедливо условие

Ф20 + Дф = я(лг + -^, (3.32)

где Д<р — фазовый сдвиг, внесенный фазовращателем. Из (3.32) с учетом соотношения

2D

фго = 2я/—(3.33)

v

получим

°=^(ы+т)+1’ <334>

v Д<р

~2f 2лГ

— отсчет по фазовращателю, выраженный в линейной мере[17].

Гетеродинная схема

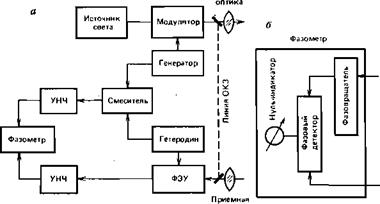
Наиболее часто встречающаяся схема построения гетеродин­ного светодальномера иллюстрируется рис. 48, а. Основным в этой схеме является то, что на модулятор и на фотоприем­ник (ФЭУ) подаются сигналы различных (но близких) частот — на модулятор сигнал частоты шм от основного генератора, а на ФЭУ — сигнал частоты ©г от вспомогательного генератора (ге­теродина). В такой схеме ФЭУ является одновременно прием­ником света и смесителем (сигнал от гетеродина подается, как правило, на внешний электрод ФЭУ, и смешение происходит в прикатодном пространстве). После ФЭУ выделяется (напри­мер, при помощи избирательного усилителя) сигнал низкой разностной частоты, фаза которого сравнивается с фазой опор­ного сигнала той же низкой частоты, полученной смешением сигналов от генератора и гетеродина в отдельном смесителе.

Пусть генератор модулирующего сигнала вырабатывает на­пряжение вида

^мод = Sin (йці ф фц). (3.36)

Для простоты анализа будем считать, что под действием этого напряжения выходящий из модулятора световой поток Ф изменяется по тому же синусоидальному закону

Ф — Фо “Ь Фм sin (о)м^ — j — фы). (3.37)

Кроме пренебрежения высшими гармониками в выражении для модулированного светового потока, мы также сознательно не обращаем пока внимания на задержки сигнала, обусловленные временем его прохождения от генератора до модулятора и инер­ционностью самого модулятора света. Далее в нашем анализе мы также не будем учитывать задержки сигнала в аппаратуре (как не учитывали их при рассмотрении предыдущих типов схем). На главный результат, который мы хотим продемонстри­ровать, это не повлияет, но сделает изложение более простым и наглядным. Вопрос об учете задержек сигнала для всех типов схем будет рассмотрен отдельно (стр. 161).

Рис. 48. • Гетеродинная схема: а — общая блок-схема; б — фазометр компенсационного типа

Вернувшийся с дистанции и принимаемый фотоприемником световой поток, очевидно, будет равен

Фпр = Ф0 + Фм sin + фм — фго)- (3.38)

Пусть, далее, гетеродин вырабатывает напряжение вида

і/гет = Ur sin (ю, і + фг). (3.39)

Под действием этого напряжения чувствительность ФЭУ, кото­рую обозначим через у, меняется по тому же закону, т. е.

Y = Yo + 7rSin((dr< + 9r). (3.40)

Мгновенное значение фототока на выходе ФЭУ определяется произведением мгновенных величин светового потока и чувстви­тельности

«ФЭУ = Фпр • Y = [Фо + Фм Sin (Ю„* + ф„ — ф2Й)1 X
х [Yo + Yr sin (a>rt + фг)] = Фоїо + Ф„Уо X
X sin (toj + Фм—фго) + ФoYг sin (art 4- фг) — f

+ у «^MYr COS [(©„ — Юг) < + (фм — фг) — фго] —

— у Ф*Уг COS [(ЮМ + ЮГ) t + (ф„ + фГ) —ф2£>]. (3.41)

Из сигнала (3.41) избирательный усилитель низкой частоты пропускает только составляющую разностной частоты £2= |юм—

—Юг|

которая поступает на один вход фазометра. На другой его вход поступает сигнал, получаемый гетеродинированием в отдельном смесителе. На смеситель подаются напряжения (3.36) и (3.39) от генератора и гетеродина. Смеситель имеет нелинейную вольт-амперную характеристику, обычно представляемую поли­номом вида i = ao+dU + a2u2>+…, где ао, Яь а2, … — постоянные коэффициенты. Обычно достаточно ограничиться квадратичным членом. Подставляя в эту характеристику в качестве напряже­ния и сумму смешиваемых напряжений (3.36) и (3.39), полу­чаем для тока на выходе смесителя

t’cM = a0 + al[UM sin (ю J + фм) + и г sin (юг* + фг)] +

—(hW и sin (<nHt + фн) —UT sin (Ю|і + фг)]а. (3.43)

Квадратичный член этого выражения содержит, в частности, со­ставляющую разностной частоты Q (образуемую от перемно­жения двух синусрв при раскрытии квадрата). Эта составляю­щая имеет вид

і’й = aJUJJT cos [Q/+(фи—фг)]- (3.44)

Она выделяется усилителем низкой частоты и подается на фа­зометр.

Таким образом, на фазометр поступают сигналы (3.42) и (3.44) низкой частоты £2. Нетрудно видеть, что они различа­ются по фазе на фго — Следовательно, в гетеродинном светодаль­номере низкочастотный фазометр позволяет измерить сдвиг фаз ф2В = ЮмТ2С, относящийся к высокой частоте модуляции Юм-

Измерение разности фаз может быть выполнено, в частно­сти, компенсационным нулевым методом; в этом случае фазо­метр состоит из фазового детектора, фазовращателя и нуль-ин­дикатора (рис. 48,6). Выходной сигнал фазового детектора в такой схеме пропорционален косинусу разности фаз входных сигналов и, следовательно, будет равен нулю при приведении

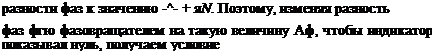фго + Дф = я(лГ + — і-|,

идентичное условию (3.32) для схемы предыдущего типа. Сле­довательно, формула для расстояния будет иметь вид (3.34)

Фазовые измерения в светодальномерах производятся ана­логовым или цифровым методом.

Аналоговые измерения выполняются, как правило, компен­сационными методами, с сущностью которых читатель уже зна­ком из материала предыдущего раздела. Компенсация подле­жащей измерению разности фаз до определенного значения про­изводится при помощи фазовращателя или оптической линии задержки переменной длины (а в дальномерах с переменной ча­стотой— изменением частоты). Оптическую линию задержки (ОЛЗ) применяют при достаточно высокой частоте модуляции света. Обычно это призменная система, удлиняющая ход луча и установленная в приемной или передающей оптике на пути светового пучка. Изменение длины ОЛЗ производится переме­щением призмы вручную или автоматически.

Большинство приборов с частотой модуляции в диапазоне 10—30 МГц содержит электрические фазовращатели индукци­онного типа. Индукционный фазовращатель — это своеобразный трансформатор с подвижной (вращающейся) вторичной обмот­кой (рис. 49). Неподвижная часть — статор — содержит две ортогонально расположенные обмотки L и L%, питаемые пере­менными напряжениями, одинаковыми по амплитуде, но сдви­нутыми по фазе на 90°. С подвижной обмотки L3 (ротора) сни­мается напряжение, сдвиг фазы которого относительно напря­жения в статорной обмотке Li определяется углом поворота ротора. Иногда ротор также имеет две ортогональные обмотки, с которых снимаются напряжения в квадратуре (т. е. отличаю­щиеся по фазе на 90°). Ось фазовращателя соединяется с от — счетным лимбом (шкала которого может быть проградуирована в условных делениях или непосредственно в единицах расстоя­ния) или с механическим цифровым счетчиком.

Аналоговое измерение сдвига фаз позволяет получить разре­шающую способность около ‘/зооо от длины волны модуляции.

При цифровых (дискретных) фазовых измерениях разность фаз. между опорным и измерительными сигналами представля­ется в виде числа импульсов. Исходные синусоидальные сиг­налы при помощи триггеров преобразуются в прямоугольные импульсы (рис. 50). Передним фронтом сформированного триг­гером импульса опорного сигнала открывается ключ, создаю­щий измерительный интервал (интервал счета), а передним фронтом измерительного сигнала этот ключ закрывается. Та­ким образом, ключ оказывается открытым на время т, соответ­ствующее измеряемому фазовому сдвигу <р=йт (Q— частота поступающих на фазометр сигналов). В то вермя, когда ключ открыт, он пропускает на электронный считчик равноотстоящие друг от друга по времени счетные импульсы, которые либо фор­мируются непосредственно из модулирующего сигнала с ис­пользованием делителей частоты, либо генерируются отдельным

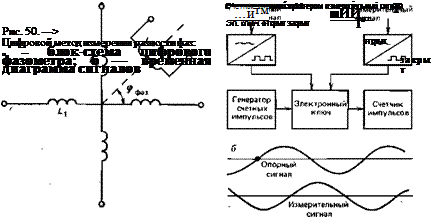стабилизированным импульсным генератором. Интервал вре­мени т определяется по числу т подсчитанных счетчиком им­пульсов как х=т-Тсч, где ТСч — период следования счетных импульсов. •

В дальномерах счетчик цифрового фазометра удобно градуи­ровать не во временной или фазовой мере, а сразу в единицах расстояния. Это достигается тем, что частоту следования счет­ных импульсов fc4 выбирают численно равной половине ско­рости света v/2 (в определенных асмосферных условиях) [18]. Дей­ствительно, так как линейная величина равна (о/2)т, а т= = mTc4=m/fC4, то при fC4=v/2 число импульсов m будет выра­жать собой непосредственно линейную величину. Для обеспе­чения десятичной системы отсчета частота счетных импульсов fc4 должна быть связана с частотой Af=Q/2n поступающих на фазометр сигналов соотношением

/с, = 10*ДЛ (3.45)

где k — целое число. Обычно k = 3, что обеспечивает точность результата до 0,001 от масштабной единицы длины, т. е. от

половины длины волны модуляции. При типичной частоте моду­ляции около 15 МГц (V2=10 м) это дает 1 см; при этом, если измерение разности фаз производится на низкой частоте Af= = 1,5 кГц, необходима частота следования счетных импульсов /сч=1,5МГц.

Для повышения точности производится не однократное, а многократное измерение разности фаз (например, 1000 от­дельных измерений, быстро следующих друг за другом в тече­ние примерно 10 с), и результаты измерений осредняются. Осредненный по многим измерениям результат выдается на электронное цифровое табло на один разряд точнее, т. е. окон­чательная точность получается 0,0001 от К/2, или от длины волны модуляции (в приведенном выше примере — 1 мм).

Цифровые фазовые измерения обладают следующими досто­инствами:

— более высокой точностью по сравнению с аналоговыми измерениями;

— высокой стабильностью при изменении внешних условий;

— удобством считывания и регистрации; .

— возможностью сравнительно простого ввода результатов измерений в систему последующей обработки (в частности, в ЭВМ) и, следовательно, пригодностью для использования в системах широкой автоматизации геодезических измерений.

Комментарии запрещены.