Бурение грунтовых зондов, установка энергетических колодцев

В САУ ланки можуть бути з’єднані в самих різних сполученнях. Проте будь-яку складну систему можна подати як сукупність трьох видів сполучення ланок: послідовного, паралельного погодженого і паралельного зустрічного.

Передаточна функція системи послідовно сполучених ланок (рис. 1.21) дорівнює до­бутку передаточних функцій цих ланок. При послідовному з’єднанні ланок вихідна величи­на першої ланки буде являтися вхідною для другої, вихідна величина другої ланки — вхід­ною для третьої і т. д.

w,(p) = —; W2 = —; W„(p) =

Xq x1 xn

Передаточна функція всієї ділянки ланцюга може бути знайдена шляхом виключен­ня проміжних змінних величин і записана у вигляді добутку

w.(p) = — = W1(p)- W2(p) — wn (p),

xn

або, в загальному вигляді

-п = W(p) = fjwi(p). (1.29)

і-1

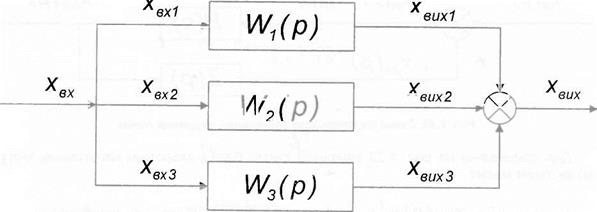
При паралельному з’єднанні ланок направленої дії вхідна величина системи одно­часно подається на вході всіх ланок, а її вихідна величина дорівнює сумі вихідних величин окремих ланок.

Рис. 1.22. Схема паралельного погодженого сполучення ланок

Для приведеної на рис. 1.22 схеми справедливо рівняння

^вих " вих1 ^вих2 ^вихЗ ■ 0 -30)

Зображення вихідних величин ланок через передаточні функції запишуться у вигляді

х<ші(Р) = Щ(Р)хт1(р);

m2(P) = W2(p)xm2(p); (1.31)

x.u*3(P) = W3(p)xex3(p).

Так як

Хе*і(Р) = Х. х2(Р) = Хтз(Р). (132)

Х, их(Р) = [ЩР) + ЩР) + Щ(Р)Хвх(р). (1.33)

В цьому випадку передаточна функція системи запишеться у вигляді

X (D) ,=л

, =Wl(p) + W2(p) + W3(p) = Xwi(P)- <134)

Хвх ( Р) І=1

тобто, при паралельному погодженому сполученні ланок передаточна функція буде дорів­нювати алгебраїчній сумі передаточних функцій окремих ланок, що входять в систему.

Паралельним зустрічним сполученням ланок називається таке сполучення, при яко­му вихідний сигнал першої ланки подається на вхід другої, а вихідний сигнал другої — на вхід першої після порівняння з відповідним знаком вхідного сигналу.

Рис. 1.23. Схема паралельного зустрічного з’єднання ланок

Для приведеної на рис. 1.23 замкнутої схеми САУ з зворотнім негативним (від’єм­ним) зв’язком маємо

(P) = [xeJp)-x33(p)]-H( р);

*зз(Р) = x. u*(P)Z(P);

*««(Р) = х. ЛР)-Н(Р)~ х, т(p)Z(р)Н(р); (1.35)

*SJP)_ Н(р) _ Н(р)

xjp) UH(p)Z(p)

де W(p) — передаточна функція розімкнутої системи.

Таким чином, передаточна функція замкнутої САУ дорівнює відношенню передаточ­ної функції прямого ланцюга до збільшеної на одиницю передаточної функції розімкнутої системи.

Для САУ з позитивним зворотнім зв’язком загальна передаточна функція має вид

х.„(Р)__Н(Р)_

х„(р) 1-W(p) ( ‘

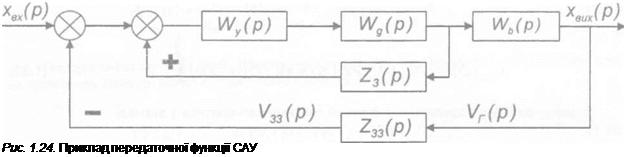Розглянемо приклад складання і перетворення передаточної функції САУ,

Для приведеної на рис. 1.24 САУ передаточні функції мають вид: — першої ланки

— третьої ланки

ланки місцевого зворотнього зв’язку

Для складання передаточної функції замкнутої системи необхідно спочатку знайти передаточну функцію разімкнутої системи W(p). Для цього умовно розіб’ємо структурну схему всієї системи на групи в відповідності з основними випадками з’єднання ланок. Пер­шою такою групою буде з’єднання ланок з передаточними функціями Wy(p) і W.(p). Об’єднавши їх, отримаємо

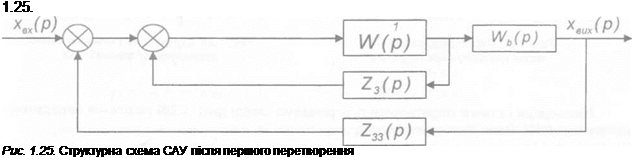Після такого перетворення структурна схема прийме вид, представлений на рис.

/

У другу групу ланок направленої дії можна виділити з’єднання W(р) і Z3(p). Після перетворення отримаємо

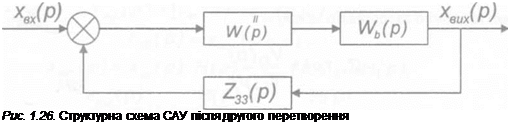Перетворена схема прийме вигляд представлений на рис. 1.26.

Передаточну функцію розімкнутої системи отримаємо після перетворення ланок W,(p) і Wb(p), рис. 1.27. Вона буде мати вигляд

ні її

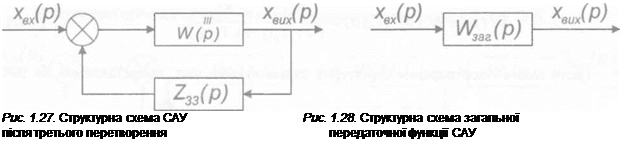W (р) — W (p)-wb(p). (1-44)

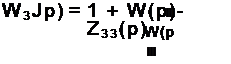Виконавши останнє перетворення, отримаємо схему (рис. 1.28) загальної передаточ­ної функції САУ. Вона буде мати вигляд

Комментарии запрещены.