Бурение грунтовых зондов, установка энергетических колодцев

Частотні характеристики отримали широке застосування при аналізі і синтезі САУ. Вирази для частотних характеристик окремих ланок і систем в цілому можуть бути легко отримані із відповідних передаточних функцій, записаних в операторній формі, шляхом заміни р на jw.

Фізично частотна характеристика замкнутої чи розімкнутої системи має місце при по­дачі на вхід системи гармонічного діяння при зміні частоти діяння від 0 до оо і збережені постійної амплітуди вхідного сигналу на всьому діапазоні зміни частот. При подачі на вхід системи гармонічного сигналу

система буде знаходитись в режимі змушених коливань. Відношення

Хвхтах, еМ®ї=(p(ja>) х

зих. тах

уявляє собою комплексну частотну функцію. Цей вираз можна розділити на речовинну і уявну частини

0(jco) = р(со) + j9(co)^ А(со)еМю}, (1.48)

де р(со),9(со), А(со),ср(со) — поліноми від (О.

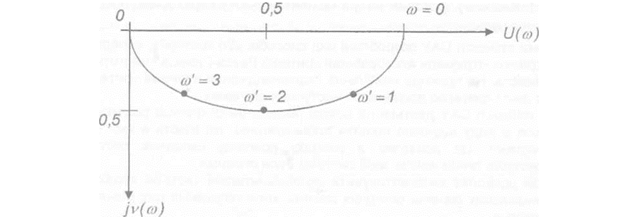
При зміні частоти со амплітуда і фаза векторів Ф(]со) будуть змінюватись, а їх кі­нець буде описувати на площині комплексну змінну криву, що уявляє собою амплітудно — фазову характеристику замкнутої системи.

У відповідності з прийнятими позначенями маємо:

р(со) — речовинна частотна характеристика замкнутої системи;

9(со) — уявна частотна характеристика замкнутої системи;

А(со) — амплітудно-частотна характеристика замкнутої системи; ср(со) — фазово-частотна характеристика замкнутої системи.

Співвідношення між ними визначаються наступними виразами:

A(co) = Jp2(co) + 92(co); ср(со) = агсІдв(о});

р(ю) (1.49)

р(со) = A(co)coscp(co); 9(со) = A(co)sincp(a>).

Цінність застосування частотних характеристик полягає в тому, що вони дозволяють побічно, без вирішення диференціального рівняння системи судити про поведінку системи в відношені стійкості і ряду показників якості, а також визначати і розраховувати засоби ко­рекції системи для отримання заданих динамічних показників.

Амплітудно-частотна характеристика розімкнутої системи уявляє собою зміну моду­ля W(jco) в залежності від частоти, а фазово-частотна — зміну аргумента вектора W (jco) від частоти вхідного сигналу со.

Визначимо амплітудно-частотну, фазово-частотну і амплітудно-фазову характерис­тики, наприклад, аперіодичної ланки. Приймемо для ланки К = 1, а Т = 2.5. Передаточна функція аперіодичної ланки приведена формулою (1.21). Замінюючи р на jco, отримаємо вирази для амплітудно-частотної і фазово-частотної характеристик:

А(со) = ~г=Т? ’

уі1 + со2Т2 (1.50)

ср(со) — arctg[W(ij)] = — arctgcoT.

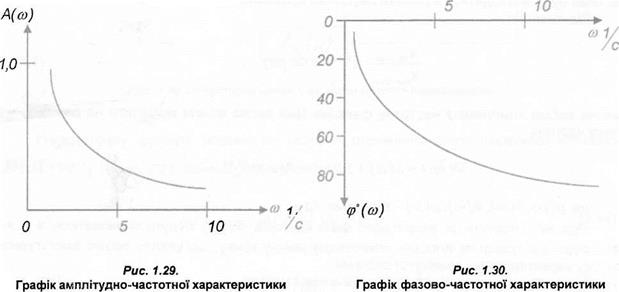Підставляючи числові значення Т, обчислюють А(со) і ср{со) для різних со, напри­клад в межах від 0,5 до 10. По результатах обчислень будують графіки (рис. 1.29, рис. 1.30, рис. 1.31).

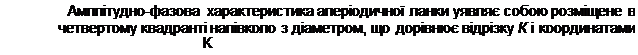центру на речовинній осі W( jco) представляють у вигляді речовинної і уявної частин

W(jco) = U(co) + jv(co);

а потім будують графік для різних значень со.

Розглянуті характеристики можуть бути побудовані як для замкнутих, так і розімкну — тих САУ, а також для окремих ланок системи. Найбільше застосування на практиці отри­мали характеристики розімкнутої системи завдяки їх наглядності і простоті побудови.

Мають також застосування тимчасові характеристики САУ. Першою важливою тим­часовою характеристикою ланки є перехідна функція. Перехідною функцією називається функція, що описує зміну вихідної величини ланки (системи), коли на її вхід подається одиничне ступінчасте діяння при нульових початкових умовах. Перехідною функцією L(t) ланки є сигнал, що отриманий на виході ланки при подачі на її вхід одиничного скачка 10(t) . Графік цієї функції (рис. 1.32) називається перехідною або розгінною характеристи­кою. Усталена складова перехідної функції характеризує статичні якості ланки.

Рис. 1.32. Графік перехідної або розгінної характеристики

Другою тимчасовою характеристикою є вагова або імпульсно-перехідна функція лан­ки. Сигнал, що отримано на виході ланки, при подачі на її вхід одиничного імпульса

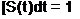( е Л

, називається ваговою або імпульсною перехідною функцією co(t) . Гра-

V.-є У

фік цієї функції є імпульсною або перехідною характеристикою.

Важливою динамічною характеристикою САУ є її стійкість. Система є стійкою, коли вона повертається до усталеного стану після закінчення діяння, яке вивело систему із цього стану. Для виконання практичних завдань система повинна бути стійкою. Математична умова стійкості системи визначається виразом

4mxc(t) 0, (1і52)

f—> со

тобто при необмеженому зростанні часу з моменту початку перехідного процесу складова хс обертається в нуль.

Для оцінки стійкості САУ розроблені ряд способів або критеріїв, серед яких найбіль­ше розповсюдження отримали алгебраїчний критерій Рауса-Гурвіца і частотні критерії Ми­хайлова і Найквіста. На практиці найбільше розповсюдження отримав критерій Найквіста. Застосування цього критерію доцільно по наступних причинах:

— оцінка стійкості САУ дається на основі передаточної функції розімкнутої системи, яка складається із ряду відносно простих співмножників, які мають в якості коефіцієнтів параметри системи. Це дозволяє в випадку розгляду складних систем вибирати параметри пристроїв таким чином, щоб системи були стійкими;

— критерій дозволяє використовувати екпериментальні частотні характеристики за­мість диференціальних рівнянь складних систем, коли складання цих рівнянь уявляє со­бою складну задачу;

— критерій зв’язує дослідження стійкості з наступним аналізом якості САУ.

Характеристичне рівняння замкнутої САУ описується рівнянням

D(p) + H(p) = 0, (1.53)

де D(p) і Н(р) — поліноми від р.

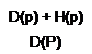Ліву частину рівняння (1.53) розділимо на D(p). Отримаємо

Позначимо в функції від р корені чисельника через р1,р2,… ,рп, а корені знаменни­ка — через р1гр2, ■■■, Рп■ При цьому вираз для W(p) можна переписати у вигляді

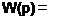
D(p) + H(p)
D(p)

1 , Н(р)_1 | к( fp-pjfp-pj-fp-pj °(Р) ( Р Рі)(Р Р2)’"(Р Рп)’

Допускаючи в попередньому виразі р = jco можна записати

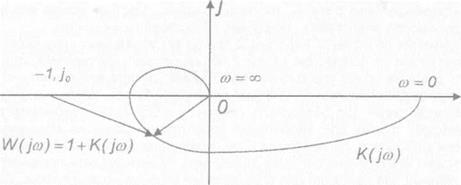
Так як кожний корінь р,. рівняння може бути представлений відповідним вектором, то при зміні со від — оо до +оо кінець кожного вектора-співмножника останнього рівняння по­вернеться на кут п. Графічно взаємне розміщення векторів представлено на рис. 1.33, де вектор

W(jco) = 1 + К( jco). (1.57)

По виду характеристики K(jco) розімкнутої системи можна судити про стійкість сис­теми в замкнутому стані. При досліджені стійкості САУ може ставитись завдання не тільки перевірки стійкості системи при заданих значеннях її параметрів, але і визначення деякої області зміни окремих параметрів, всередині яких система залишається стійкою. Встанов­
лено, що якщо характеристика K(jco) не охоплює точку з координатами [~1,j0, то сис­тема буде стійкою, і система буде нестійкою, якщо характеристика охоплює точку з коор­динатами [-1, j0].

Рис. 1.33. Розміщення векторів М(]ш) і К(]ш)

Комментарии запрещены.