Гидравлическая характеристика буровых растворов. Элементы реологии
Гидравлическая характеристика буровых растворов. Элементы реологии
Значительное большинство применяемых буровых растворов по своим свойствам во многом отличается от обычной воды. Несмот** ря на это, все они могут быть названы жидкостями, ибо с точки зрения гидравлики жидкостью являются любые тела в состоянии текучести: несмотря на ризличие их молекулярной структуры, они рассматриваются как сплошные среды с непрерывным (как правило) распределением в них основных физических свойств. .
Если .выделить мысленно внутри жидкости некоторый объем, находящийся в состоянии равновесия (если жидкость находится в движении, то необходимо учесть силы инерции и сопротивления*, и рассмотреть силы, которые действуют на него, то можно обнаружить, что эти силы могут быть двоякого рода. Первые из них —> это поверхностные, т. е. такие силы, которые распределены по поверхности выделенного объема жидкости и по своей величине пропорциональны поверхности. К ним должны быть отнесены силы трения, упругости, поверхностного натяжения, давление окружающей среды и т. п. Вторую категорию составляют объемные (массовые) силы, действующие на всю массу жидкости или, точнее, на каждую частицу выделенного объема. Это, например, сила тяжести, силы инерции и т. д.
В общем случае вектор какой-либо силы JR, действующей на определенной площадке da, образует с внешней нормалью к этой площадке некоторый угол и поэтому может быть разложен на две составляющие — нормальную Р и касательную Т.
Нормальная составляющая вызовет деформацию сжатия. Напряжение сжатия обозначается буквой р и называется гидродинамическим давлением, если наблюдается в движущейся жидкости, и гидростатическим давлением, если жидкость находится в покое. В частном случае, когда давление распределено равномерно,
р — Р/(0. (II* 1)"
Составляющая Г вызывает касательное напряжение (г—Т/а), т. е. напряжение трения или деформацию сдвига. Свойство среды сопротивляться деформации сдвига называется вязкостью. Это свойство противоположно текучести. Поскольку идеальная жидкость предположительно обладает абсолютной подвижностью, то в ней отсутствует касательная составляющая и не может быть свойства вязкости.
Для измерения касательных напряжений пользуются теми же единицами, что и для измерения давления. При этом, если отсчет ведется от абсолютной пустоты, то давление называется абсолютным, а при отсчете от давления окружающего нас пространства (т. е. от атмосферного давления) его называют избыточным или манометрическим. Давление ниже атмосферного называется вакуумом.
|
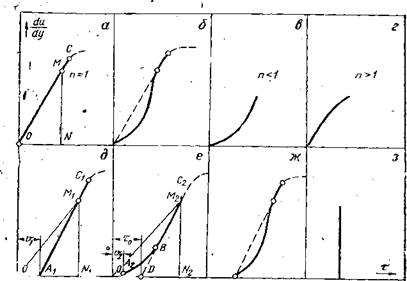
Рис. 1. Различные типы аномальных тел: а —- ньютоновская жидкость; б — тело Оствальда; в — псевдопластичная жидкость; г — дилатантная жидкость; д — вязко-пластичная жидкость (тело Бингама); е—аномальная > вязко-пластичная жидкость (тело Шведова); о» — тиксотропнопластичная жидкость; з— Хрупкое тело |
Ф. И. Шведов на примере разбавленных золей желатины впервые описал «несовершенные» жидкости, совмещающие в себе свойства жидкостей и твердых тел, которые с равным основанием можно назвать «несовершенными» твердыми телами. Тем самым были заложены основы реологии[1], которая занимается изучением 1
деформаций таких «аномальных тел». г
Различные жидкости могут быть аномальными во многих отношениях, однако все они занимают промежуточное положение между идеально вязкими (ньютоновскими) жидкостями и идеально хрупкими твердыми телами (рис. 1). Последние характеризуются, полным отсутствием текучести и разрушаются, как только величина приложенного напряжения по своей величине переходит определенный предел. Этот предел, при котором тело под воздействием приложенных внешних сил теряет способность восстанав- ;
-ливать первоначальную форму (необратимая или остаточная деформация), называется пределом линейной упругости или пределом пропорциональности. При этом под упругостью понимается ■ свойство тел восстанавливать первоначальную форму при снятии деформирующей нагрузки. Соответственно тёлй, обладающие свойством упругости, называют упругими телами.
В случаях, когда при постоянной нагрузке, превышающей предел упругости, тело медленно деформируется, принято говорить, что тело течет, а деформацию называть пластической. При этом напряжение, при котором тело начинает течь, называется пределом текучести, а само тело, обладающее заметной остаточной деформацией и текучестью, называется пластичным.
Течение представляет собой один из видов[2] деформации, при котором величина деформации непрерывно возрастает под влиянием постоянно действующей силы.
Таким образом, в общем случае величина деформаций, как и их характер, зависит от свойства тела, величины’ нагрузки, ее на* правления и т. д.
Реология устанавливает взаимосвязь между силами, действующими на материальное тело, и деформациями, вызванными этими силами. Основной задачей реологии является установление функциональных зависимостей между градиентом скорости течения du/dy и напряжением сдвига т. Кривые, графически отображающие указанные за! висимости, называются реологическими, а сами зависимости — реологическими уравнениями состояния.
В настоящее время известно множество разнообразных уравнений состояния, или, как их иначе называют, моделей. Также известно немало попыток дать единую классификацию реологических тел. Одной из распространенных является классификация Доджа, который в зависимости от характера реологической кривой предложил делить Лидкости на следующие три большие группы.
1. Жидкости, для которых скорость сдвига зависит только от приложенных касательных напряжений. Подобного рода системы описываются реологическим уравнением типа
и называются реологически стационарными жидкостями’
2. Жидкости, реологические характеристики которых зависят от времени действия касательных напряжений. .
Жидкости этой группы являются реологически нестационарными и в общем случае могут быть описаны уравнением вида
‘ ‘ * f=/(r, t). (И. З)
3. Вязко-упругие жидкости, т. е. такие, которые обладают свойствами как твердого тела, так и жидкости и частично упруго восстанавливают формы после снятия напряжения.
Для описания подобного рода жидкостей Максвелл предложил аддитивно объединить закон Гука и закон Ньютона в одно реологическое уравнение состояния:
TOC o "1-5" h z V = — + jr. (В-4)
ц G
где G — модуль сдвига. .
Типичным примером максвеллова тела может елужить смола (сапожный вар). •
Как показывают наблюдения, в нефтепромысловой практике приходится иметь дело в основном с жидкостями первой и второй групп.
Известно высказывание Максвелла, согласно которому различие между твердыми телами и жидкостями наиболее верно определять по результатам действия силы тяжести. Исходя из такой предпосылки, Н. В. Тябин, базируясь на выведенном им общем уравнении течения вязко-пластичной среды, доказывает существование некоторой величины
9 0 „
2кр — — * (В-5)
Р£ V ■
которую он называет критической высотой формосохраняемости (0—предельное напряжение сдвига; р — плотность; g— ускорение свободного падения). При этом, по мнению Н. В. Тябина, произведение pgzKV выражает то критическое значение потенциальной энергии, которое может накопиться в данной ср*де. При pgz> >pgzKp часть накопленной потенциальной энергии превращается в кинетическую энергию течения.
Таким образом, при z>zKp среда представляет собой вязкопластичную жидкость, для течения которой по всем возможным направлениям достаточно воздействия одной только силы тяжести. Будучи заключенной в сосуд, она принимает форму этого сосуда.
При 2<zKр среда ведет себя как вязко-пластичное тело, т. е. сохраняет свою форму под действием силы тяжести, но вязкопластически течет при напряжениях больших напряжения сдвига.*
Р. И. Шищенко приводит следующую классификацию вязкопластичных сред, в основу которой положено отношение 0/у:
е/V. см. 0,5 0,5—2,0 2—15 15
Вид Структурные Жидкие Густые ‘ Твердые тела,
среды жидкости пасты пасты вязко-пластичные
• тела