Бурение грунтовых зондов, установка энергетических колодцев

Ранее (см. гл. II, § 3) было получено уравнение расхода вяз­кой жидкости в виде выражения (11.23). Ради удобства примем R = b. Тогда пЬ*р

(11.23′)

8 ц1

Из этой формулы непосредственно видно, что зависимость гра- фически должна изображаться прямой, проходящей через начало координат (прямая 1 на рис. 21). Определяя значение средней ско- рости Q РЬ2

8/ц

из которой вытекает, что при ламинарном режиме, т. е. для зна­чения Re<2320 Х= 64/Re. (VI.2) Что касается зависимости Q=f(p) для случая, когда по круг­лой трубе перекачивается вязко-пластичная жидкость, подчиняю­щаяся закону Шведова — Бингама, то согласно выражению (II.24) •она должна иметь следующий вид: • = nR*P Г __i j%_ _J_ ( т0 у] 8rl L 3 тс 3 ^ тс / J

(VI. 1)

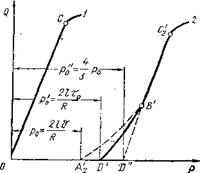
Рис. 21. Зависимость давления от расхода в круглой трубе. Режим: / — ламинарный; 2 — турбулент­ ный

я р заменяя h, из (VI. 1) найдем: * 8ц1и 32fx2v

уЬг

yd2

После умножения числителя и знаменателя на 2 vg с учетом (IV.11) это выражение легко мо­жет быть приведено к виду фор­мулы Дарси — Вейсбаха:

& 2g

64 Re

I v4 — = X, d 2gd ’

h =

Движение вязко-пластичной жидкости может начаться только — после преодоления характерной для нее величины то. Следователь­но, в круглой трубе при значениях г, для которых т<До, течения такой жидкости не будет (рис. 22). Обозначая г0 радиус цилиндра, на внешней поверхности которого соблюдается равенство т=т0, на основании (11.18) можем получить: ’

2/т„

Очевидно, что вязко-пластичная жидкость, находящаяся внутри объема, описываемого радиусом г0, должна двигаться как одно. ~ w целое, т. е. после начала движе­

	г0 /	< << ГГ.
	(	иО	——-
—————
Г"
		ттгг?’, ,,,.,,

Рис. 22. Схема распределения ско­ростей и касательных напряжений в круглой трубе при структурном режиме

ния жидкости в середине трубы образуется цилиндр с неразру­шенной структурой радиусом (ядро потока), имеющий ско­рость, которую обозначим через Ыо — Между ядром и стенками тру­бы образуется градиентный слой, напряжения в котором больше, а скорости, наоборот, меньше, чем в ядре. Следовательно, ско­рость ядра является одновремен­но и максимальной скоростью потока, т. е. при структурном дви­жении жидкости итах—щ. ‘

Обозначая р0 давление, при достижении которого начнется дви­жение раствора (при г=Ь), можно записать:

: Ро*

Ь

(VI. 4)

(VI. 5) (VI. 6>

Сравнивая эту величину с зависимостями (IL19) и (VI.3), убеждаемся, что

rjb = Ро/р = т0/тс.

Поэтому (11.24) представим в виде

л64р

8т]1

или, используя обозначения, принятые в (IV.41):

(VI • 7)

nb*p

/(Р) = <2оШ»

(VI. 8) (VI. 9)

7(Р); иП

h =

2 gd ’

Далее, поступая так же, как и в случае ламинарного режима последовательно находим: Q

я Ь2 84/ 64 vH

R е/(Р) 2gd

= —

64 64

Jt= — =——————— , (VI. 10)

Re/(P) Re[12]

где, следуя Э. К. Латыпову и Б. С. Филатову,

Re** = Re/(p)i

Однако выражение (VI.9) может быть использовано только в том случае, когда величина р наперед задана. Если же она подле­жит отысканию, то эта зависимость теряет свой смысл, так как в состав самой величины р входит искомая величина р.

Выражение для точного определения р было дано Б. И. Ми — Тельманом и Г. Д. Розенбергом на основании анализа выражения (VI.6):

P = — j — Ф(И), (VI. II)

из которого в результате сопоставления с формулой Дарси — Вейсбаха вытекает, что

———— 1—— (VI.12)

3 ЯшФ(И)

где

Яш = Р^/То! И = T0d/r)U.

Однако выражение для <р(И) в развернутом виде столь гро­моздко, что практическое использование формулы (VI.12) весьма затруднено. Менее громоздкую формулу для определения X пред­ложили Н. П. Лещий и Д. Ю. Мочернюк:

(VI.13)

л-=^г[1+4(,^’л,+и)]-

Как правило, р^>ро и поэтому третьим членом в скобках выра­жения (VI.6) пренебрегают. Тогда

я б4 / 4 я Ь[13]р ( 4

Как показывает анализ, использование упрощенной зависимо­сти (VI.14) вместо точной (VI.6) допустимо при р^0,5. Получаю­щаяся при этом погрешность не превышает 6 %*.

Решая (VI. 14) относительно р и используя зависимости (VI. I), (VI.4) , а также (III.8), можно получить: 32и… h =———— !г-+———— —. (VI.15)

г1 16 d* ^ 3

у а* б dy Сопоставление полученного выражения с формулой (III.20) дает 64rig

_ 64 )~ Re* ’

Х = —

(VI .16)

yvd

бтр

где

(VI. 17)

Зависимости (VI.16) и (VI.17) широко известны в расчетной практике. Однако они выведены из упрощенного уравнения (VI, 14) и поэтому являются приближенными, а па- раметр Re*, строго говоря, не является кри- терием подобия. . Нами совместно с Г. Г. Габузовым [68] предложена методика определения величины Re** по формуле 86 ‘ — (VI. 18)

Рис. 23. Зависимость И от Р

Re** = Re-

И

которая получается путем ряда преобразова­ний из выражения (VI.8). Параметр Ильюшина можно получить по формуле (VI.19)

И =

Этот параметр довольно легко вычислить, зная свойства глинистого раствора (ц, то), диаметр трубы d и расход жидкости Q, по формуле

nd3r0 4Qt]

(VI.20)

И:

VX]

Зная же величины параметра Ильюшина, по формуле (VI.19) или по заранее составленному на основании этой формулы графи­ку (рис. 23), очень просто определить величины р и 8р/И, необхо­димые для отыскания Re** без каких-либо допущений.

Комментарии запрещены.