Бурение грунтовых зондов, установка энергетических колодцев

Интересно собрать воедино величины общей механики, разве­дочной геофизики [137] и специфические величины ГТИ с це­лью выяснения их взаимосвязи и физической сущности.

С целью упорядочения написания получающихся при этом производных параметров введем очередность написания симво­лов в формулах (табл. 3.2).

Составим таблицу физических величин, рекомендуемых к оп­ределению при проведении ГТИ (табл. 3.3). В таблице даны ве­личины и их единицы СИ как непосредственно определяемые измерением, так и получаемые на основании метода размерно­стей как производные величины.

Для удобства последующей обработки производные величи­ны отнесены к четырем измерительным комплексам.

Комплекс 1 — обязательный (ОК), включает преобразовате­ли Ь, Г, V, С, Р, С? (табл. 3.1), комплекс 2— включает в себя ОК+ДК1 (р, V), комплекс З— ОК+ДК2 (/", А), а комплекс 4 — ОК+ДК1+ДК2.

В конце таблицы особо выделен комплекс 5, включающий обяза­тельный комплекс (ОК) и дополнительный комплекс 3 — ДКЗ (/ °, Гс), по размерностям не связанный с ранее упомянутыми измерительны­ми комплексами — объединение всех измерительных комплексов по­зволяет получить полный измерительный комплекс.

Из рассмотрения табл. 3.3 видно, что применение метода раз­мерностей уже на первом этапе позволяет получить значитель­ное количество наиболее простых по структуре производных еди­ниц, более чем на порядок превышающих количество основных величин ГТИ. В табл. 3.3 не вошли специфические величины ГТИ [81, 83], имеющие размерность физических величин. Они показаны в табл. 3.4. Кроме того, наряду с безразмерными вели­чинами, полученными в табл. 3.3, имеется целый ряд безразмер­ных величин ГТИ, часть из которых выведена Э. Е. Лукьяновым ранее [81, 83]. Физическая сущность некоторых безразмерных величин ГТИ раскрыта в табл. 3.5.

Анализ табл. 3.3, 3.4, 3.5 показывает, что применение метода размерностей дает возможность получить около двухсот относи­тельно простых по структуре производных величин ГТИ, имею­щих физический смысл. В связи с этим интересно выяснить ин­формационный вклад параметров ГТИ с непосредственным изме­рением для получения производной информации.

Таблица 3.2 Очередность написания символов в формулах № л/п Сим­ вол Размер­ ность Эквива­ лентные символы Обозначение величины 1 1 L /,//,/; Д Длина, смещение, глубина, диаметр 2 т М Масса 3 Т т ? Время 4 / т-1 /7, СО Частота колебаний, частота вращения, угловая скорость 5 V LT-‘ V Скорость 6 А it-1 Ускорение (#— свободного падения) 7 в LMT-2 Т7 Сила, вес, нагрузка 8 Р L-‘MT-2 Р Давление, механическое напряжение 9 0 L3T~’ <7 Расход объемный 10 Б L2 5 Площадь 11 Ф V К Объем, вместимость 12 IV L2MT-2 Л Работа 13 N UMT~l Р Мощность 14 Е L2MT Энергия 15 Р LMT-‘ Количество движения, ИМПУЛЬС силы 16 М L2MT-2 Момент СИЛЫ 17 J L2M Момент инерции 18 К L2MT-‘ Момент количества движения 19 р L-4I Плотность 20 у L-t-MT-2 Удельный вес 21 м L-‘MT-‘ Динамическая вязкость 22 и UT Кинематическая вязкость 23 е 0 1°,Ы° Терм од ин ам и ческая тем и ература, температура в градусах Цельсия 24 N г моль Количество вещества (содержание газа в газовоздушной смеси)

Физические величины, рекомендуемые к определению при проведении ГТИ, и их единицы № п/п Величина Единица СИ Г Непосредственно 1 определяег1ые величины Производные единицы Наимено­ вание Раз­ мер­ ность Наимено­ вание Обоз­ наче­ ние Выраже­ние через единицы СИ Измерительные комплексы Комплекс 1 обязательный (ОК) Комплекс 2 (ОК+ДК1) Комплекс 3 (ОК+ДК2) Комп­лекс 4 (ОК+ ДК1+ ДК2) 1 2 3 4 5 6 7 8 9 10 11 1 Длина (смещение) глубина, высота ь Метр м м ц Не, йе — V (5ри й У’~(Г’Ури V /с /’ур’ Ро. ро УА ‘ АР /А У ОР 2 Масса м Килограмм кг кг ‘ <7 а Л’/2 Ор / 3 Время т Секунда Минута Час с мин ч с 60 с 3600 с т, *6> ^кв*•■ V 1 А ’/ 4 Кривизна Метр в ми­нус первой степени 1/м м_| — — V С Уру и ‘ бри ‘ 6 / V? V’ /в’ УА АР р<2’рс г Ор У (7

1	2	3	4	5	6	7	8	9	10	и
5	Площадь (потенци­ал смеще­ния)	и-	Квадрат­ный метр	м2	м2	—	С (? Р’ У	—	/0 УА А V3	—
6	Объем	О	Кубичес­кий метр	м3	м3	Ф, Ус	У Р	—	0 У<2 /’ А	—
7	Скорость, декремент поглоще­ ния	пл	Метр в секунду	м с	М-С~’	У	І ^ 0 7” (7 ’5	<7		/А Лр
8	Ускорение	1Т-	Метр на секунду в квадрате	м	М’С~2	А	—	—	/2С /2е	/р Кр’ Лр
9	Сила, нагрузка	нат1	Ньютон	Н	М-КГС~2	О	РО У	К(2р, і (фи	Р{2 £Лр Д ’ /2	—

е

Продолжение табл. 3.3 1 2 3 4 5 6 7 8 9 10 11 10 Давление, механи­ческое на­пряжение, модуль Юнга, мо­дуль объ­емного сжатия 5= ч Паскаль Па М_|-КГ-С’2 Р (7 У 0 К2р /2с 110 АУ ’ 0 ’ АС7 /2С /с ’ и УАр / ’ ЬАр, ЦУр, ҐОр V 11 Объемный расход 1?Т’ Метр ку­бический в секунду м^ с м3-с’ 0 К5,™ Р ри ЬУА Ґ- (7 Ц> 12 Плот­ ность 1-Ш Килограмм на куби­ческий метр кг м3 КГМ’3 р (7 У<2 (7 і У V /Р С УА ’ /УА2 ’ (7 ЄР — Ь/С’ ЬУАО 13 Количес­тво дви­жения ІМТЛ Килограмм- метр в секунду м кг—— с М-КГ-С’1 (7 УЄ /’ А 14 Импульс силы 1МТЛ Ньютон- секунда Не М-КГ-С*1 — — — _ _

і	2	3	4	5	6	7	8	9	10	11
15 16	Работа, энергия (кинема­тическая и потен­циальная) Момент силы	имтг	Джоуль Ньютон- метр	Дж	М2’КГС’2				КС Р<2 / ’ /	ЄР0 £/1рг> ’ £К2 рг>
имтг	Нм	М2’КГС 2					/
17	Мощность, поток энергии волн	имг-	Ватт	Вт	М2-КГ-С’3		РО, КС		£К2ри
18	Период колеба­ ний	т	Секунда	с	с	г	—	—	К 1 А ’ /
19 20	Частота колебаний Коэффи­циент по­глощения	г1 7м	Герц Секунда в минус пер­вой степени	О 1 — —1 с	С’1 С’1	/	V	—	А ІЇ. АР VI С ’ ІІУА е	УАр Р ‘ С
21	Гравита­ ционный потенциал	и-т-2	Джоуль на килограмм Квадратный метр на секунду в квадрате	Дж кг 7 м~ т~ С"	М2’С~2	—	—	—	іаЛ, / /2<2 к	1Л2Р /»

ІІИІ и 111 ‘.Пі «і

Продолжение табл. 3.3 I 2 3 4 5 6 7 8 9 10 11 22 Вторая производ­ная грави­тацион­ного по­тенциала т- Ньютон на килограмм- метр я с-2 — — — Г2 /А У, у — (кг • м) 23 Плотность потока энергии волн МТЪ Ватт на квадрат ный метр Вт м2 кг-сэ — — — АО IV — 24 Момент инерции 1?М Килограмм — метр в ква­драте КГ’М2 М2’КГ СО К4 02р л 25 Момент количества движения, импульс момента силы и-мт-1 Килог — рамм-метр в квадрате в секунду т м~ кг—— с м2-кгс_| — — — СО уро ЬА ’ /А ’ 10 СК / ’ Ґ — 26 Жесткость МТ-2 Ньютон на метр я м кгс2 — — — АС [АС К4С К2 ’ /0 ’/2С — 27 Волновое сопротив­ление (акусти­ческая же­сткость) £-2Л/Г’ Килограмм на квадрат­ный метр в секунду кг М’2’КГ-С"2 — с 0 — /с £К2 — м‘ • с

1	2	3	4	5	6	7	8	9	10	11
28	Коэффи­ циент сопротив­ ления	МТ’	Ньютон — секунда на метр	н — м	КГС’1	—	с к	—	/с с ‘и	—
29	Динами­ ческая вязкость	і’МГ	Паскаль- секунда	Пас	м’-кгс-1	и	Ю С 0 ЧК’ ІР V	Си т	УР УвР А ‘Ь/АО’ АЄ Ув Р<2 ’ /0 ’ рс УА	—
30	Кинема­ тическая вязкость	итл	Метр в квадрате в секунду	м2 с	м2-^1	1)		с ЬУр	У2 1.А / ’ /
31	Удельный вес	ьш1	Килограмм на квадрат­ный метр — секунду в квадрате	КГ	М’2’КГС’2	У		С Р ЬУ<2	/Р АС У ‘ К0 ’ /С С 0 ’ /К4	04 £Ки ’ /2С Уу
2 2 м с

Продолжение табл. 3.3 1 2 3 4 5 6 7 8 9 10 11 32 Безраз­ мерные величины 0 КС К51 ’ Р(2 £С Г шЛ Орт 1 Оц; с Iе] £Уру 1£У/л ) /к к А’Ц’ АЄ /РО ІР К4р ’ ЬЛР рс’ і АР Р ‘ 1,УН Р<2 ‘ С ЦОр 33 Термоди­намичес­кая темпе­ратура (т-ра в °С) е (0 Кельвин Г радус Цельсия К °С К (Ґ+ +273,15) Комплекс 5 (ОК+ДКЗ) 34 Количес­тво вещес­тва (соде­ржание га­за в газо­воздушной среде) /Уг Моль моль моль С.+ С 1 п

Размерность специфических величин ГТИ № п/п Наименование величины Размерность Выраже­ние через единицы СИ Выражение величины 1 2 3 4 5 1 Коэффициент фильт­рации (размерность проницаемости) и м2 КИ,-КЯ1 Л к Аф‘ “ ± АН ~ АН ь, х) ./*А0 ф2 “ К — к 2 Параметр фильтрации (размерность проницаемости) и м2 П ф — АГбо * 3 Термоградиент к/м (°С/м) д©. дг дя ’ дя 4 Удельная энергоемкость ь-‘мт-1 джоуль м3 . N. АР<2 ЫОр у га, К5 з 5 Нормализованная скорость (по забойной мощности) 1_М1Т2 м3 джоуль КУ3 КЛ’з N Л^з Д/>0 /^Ср 6 Дифференциальный расход итА м3(литр^ С 1 с ) А0 = ±(0в-авых)

Продолжение табл. 3.4 1 2 3 4 5 7 Коэффициент гидравлического сопротивления £-2 ч М ^ММ’У р аг ~ Г)1 „ Увх ‘ Р вх ‘ 8 Коэффициент эффективного сечения гидравличес­кой системы (коэффи­циент утечки ПЖ) Ь2 м2(мм2) ♦ /3 ^ВХ Рй /> 9 Время«отставания» (время эвакуации забойной порции ПЖ до первичного пре­образователя инфор­мации в гидравличе­ской системе) Т с(мин) Г°т (9™ (с)’ Т°т ~ 16,6 п" (МИН>’ *£вых >^ВЫХ где Уш — объем затрубного пространства, м3; <2„ых — расход ПЖ на выходе из скважины, м3/с 10 Скорость: 10.1. Механическая 10.2. Рейсовая 10.3. Общая (коммерческая) 1ТЛ м/ч м/мин м/ч м/ст. мес V — Н ; V Д/г; V Н т5 д/ р ^ + 7; + Твсп где 7^п — время на вспомогательные операции; Гс — продолжительность спуско — подъемов долота; УЛЮ=7-^-, кал где Гкал — календарное время бурения скважин

Физическая сущность некоторых безразмерных величин ГТИ № п/п Выражение величины Название Сущность 1 2 3 4 1 г РО Коэффициент реа­лизации гидравли­ческой мощности Отношение реализованной на забое мощности к гидравлической мощности. Характеризует зависимость буримости породы от основных параметров процесса 2 II о. Коэффициент разбавления Отношение расхода ПЖ к объему выбуренной породы в единицу времени. Характеризует величину разбавления флюида из выбуренной породы промывочной жидкостью 3 II о : ^ Коэффициент обогащения ПЖ шламом Отношение объема выбуренной породы в единицу времени к расходу ПЖ. Характери­зует степень обогащения ПЖ шламом 4 к с 1АР 31 //0р’ 32 /2С Коэффициенты загрузки турбобура Характеризуют степень загрузки турбобура (забойного двигателя) от сочетания основных параметров процесса 5 К = и р /р Коэффициент интенсивности разрушения Отношение производной по механическому напряжению к производной по давлению в гидравлической системе. Характеризует интенсивность разрушения горной породы в конкретных условиях скважины (забойную прочность) 6 £ УА 6 Коэффициент буримости К6 имеет сходство с Ки р, дополнительно учиты­вает влияние глубины скважины и более глубоко связан с динамикой работы долота на забое

Продолжение табл. 3.5 1 2 3 4 7 К ° КпЖ ~ £Крг, Коэффициент влия­ния свойств промы­вочной жидкости Характеризует степень влияния свойств ПЖ на процесс разрушения в реальных условиях скважины 8 к Коэффициент динамичности Отражает влияние на процесс бурения динамики работы долота на забое. Является отношением ускорения углубления скважины к ускорению колебаний верха бурильной колонны 9 II О о Относительный коэффициент буримости Отношение скорости бурения за небольшой интервал времени Д/ к текущей скорости бурения (средней скорости бурения) за время / от начала рейса. В значительной мере снимает влияние состояния долота и режима бурения и рельефней выделяет различия в буримости горных пород 10 % 1 1 Л/>р Относительный коэффициент гидропроводности Основан на отношениях фактического и расчетного изменения давления в гидрав­лической системе при вскрытии пласта — коллектора 11 Пб = ^бо ‘ к. Параметр буримости Безразмерный параметр, являющийся произведением относительного коэффициента буримости на относительный коэффициент гидропроводности. Учитывает изменения как механических, так и фильтрационных свойств горных пород

1	2	3	4
12	П м= ‘ ^ПЖ = 75———— Qpv	Параметр момента силы	Является произведением К5 на К при замене А//1 на /, превращается в Ю/Ори, где £(7 — момент силы механической, Qpv — момент силы гидравлической. Отношение моментов силы — безразмерный параметр, характери­зующий соотношение гидравлических и меха­нических характеристик системы по стволу скважины
13	у ^(^150-400) ПС л 60—400	Коэффициент песчанистости	Отношение виброускорения в диапазоне частот 150—400 Гц к виброускорению в диапазоне частот 60—400 Гц. При бурении песчаников максимум энергии колебаний смещается в низкочастотный диапазон, поэтому К на песчаниках уменьшается
14	К = К (1-Л у по по. та.х уо’	Коэффициент открытой пористости	Кпотах— максимальная пористость неуплотнен­ных осадков в верхней части разреза (Кпо. тах — 0,4 [40% 1). Ат — относительная энерго­емкость горной породы. Ауо = Ау/А тах, где А’ — энергоемкость для изучаемой породы разреза; А[ах — энергоемкость глинистой покрышки (опорный репер), определенная в данном долблении или в сходных условиях по соседне­му долблению; п — показатель степени, п = 1,7 — 2,7 в зависимости от интенсивности уплотнения осадков в конкретном разрезе. Кп0 характеризует открытую пористость в широком диапазоне ее значений.

Продолжение табл. 3.5 1 2 3 4 15 Г РвХ РиЫХ Ко РсГГ /ПЖ — О Г ох Рвх — Р пых + ТГ’Рс Рю, Коэффициент газосодержания ПЖ Определяется методом объемной гамма — плотнометрии с учетом коэффициента обога­щения ПЖ шламом. Плотность скелета породы определяется по образцам шлама или принимается равной рсп= 2,5х103. Г1ж определяется отношением объема, занимаемого газом, к полному объему смеси. Безразмерен [м3/м3; см3/см3] 16 Лю ~ ^ПЖ ‘ Кр = Гпж ■ Коэффициент остаточной газона — сыщенности породы (приведен к атмос­ферным условиям) Определяется как произведение коэффициента газосодержания ПЖ на коэффициент разбавле­ния. При определении Гпо могут использоватться значения определенные как по результатам объемной гамма-плотнометрии, так и по резуль­татам измерения градиента давления, акустичес­ким методом и т. д. Характеризует остаточное газосодержание горной породы [м3/м3] 17 ОПУС-С2^з><С4хС5 х С,(С2 + высш) х!00 Обобщенный пока­затель углеводород­ного состава (ОПУС) Характеризует разницу углеводородного состава одним значением, которое увеличи­вается с увеличением «жирности газа». Приме­няется для любого числа компонентов п, значение С,— Сп которых отсчитывается в относительных процентах. Базразмерен [%%] 18 ОПУС3 = С| хС1 ; (С2 + С3) ОПУС4 = С, хС2хС3 (С 2 + с3 + С4) Применяется для случая загрязнения ПЖ добавками нефти, когда тяжелые углеводороды неинформативны. С увеличением «жирности» газа значения ОПУС3, ОПУС4 уменьшаются. Безразмерен [%%]

В условиях, когда получены десятки новых параметров ГТИ, имеющих физический смысл, но информационная ценность ко­торых для решения задач ГТИ еше не выяснена, логично не при­менять методы экспертной оценки или какие-либо другие мето­ды ранжирования ценности информации, как это делалось авто­ром ранее [83], а сделать допущение информационной равно­значности всех основных и производных величин ГТИ.

Из теории информации известно [110], что количество ин­формации, равное разности исходной и оставшейся после изме­рения энтропий, записывается для случая равномерного закона распределения плотности вероятности как

/ = Н(Х) — Н(Х/ХП) = log(X2 — Xt)~

— log 2А = log Xl ^ X[ = — log x, (3-6)

где Н(Х) — энтропия, характеризующая неопределен­ность измеряемой величины перед изме­рением (исходная энтропия);

Н(Х/Х„) — энтропия, характеризующая неопределен­ность, оставшуюся после получения пока­зания прибора (условная энтропия);

Хь Хг — начало и конец диапазона измерения;

±Д — абсолютная погрешность измерения.

Единицы измерения как энтропии, так и информации зави­сят от выбора основания логарифма в приведенном выражении. При использовании десятичных логарифмов единица измерения называется — дит, в случае двоичных логарифмов — бит, а при использовании натуральных логарифмов — нит.

Учитывая, что на данном этапе рассмотрения проблемы, ко­гда отсутствуют сведения как по диапазонам измерения вновь полученных величин, так и по абсолютной погрешности приме­няемых измерительных средств — А, применять общепринятые в информационной теории измерительных устройств единицы информации невозможно.

Поэтому на данном этапе введем понятие условной единицы информации (УЕИ), которое применительно к проблеме получе­ния информации при ГТИ может быть сформулировано следую­щим образом.

Условная единица информации равна количеству инфор­мации, получаемому при условии протяженности диапазона измерения х2 — *1 в 50 единиц шкалы и абсолютной погреш­ности измерения Д = 2,5.

Тогда при использовании десятичных логарифмов

УЕИ = 1ё *2 2д Л‘ — 1и= ЫЮ ° 1дит. (3.7)

Сделаем допущение, что как основные, так и производные физические величины обладают информативностью в 1 УЕИ (1 дит), т. е. информативно равнозначны между собой.

Составим таблицу информативности основных параметров ГТИ (табл. 3.6), представляющую собой матрицу измеряемых па­раметров и производных определяемых параметров. На пересе­чении определяется количество случаев применения измеряемых параметров для получения производного параметра, взятое из табл. 3.3, 3.4, 3.5.

Например: измеряемый параметр Ь один раз применяется для определения Ь, 1 раз — для определения т, 4 раза — для опреде­ления /, 5 раз — для определения V и т. д.

Столбец справа (2) и нижняя строка (2) матрицы представля­ют собой сумму случаев применения конкретного измеряемого параметра и сумму случаев применения измеряемых параметров для определения конкретного производного параметра, соответ­ственно.

Общее число параметров (без параметров комплекса 5) состав­ляет 190, общее число случаев применения измеряемых парамет­ров — 476. Следовательно, суммарная информативность парамет­ров 4 комплексов составляет 190 УЕИ, а средняя информативность 1-го измеряемого параметра в производных параметрах

Успп =^™ 0,399 = 0,4УЕИ.

Исходя из этого, в табл. 3.6 показана информативность ка­ждого измеряемого параметра в группе задач, решаемых 4 из­мерительными комплексами, а также информативность про­изводных параметров в этой группе задач (строка ниже мат­рицы).

| Измеряемый, параметр	Производный определяемый параметр, символ или порядковый номер в табл. 3.3	Информатив­ность, УЕИ
1.	т	Т	/	V	А	С	Р	<2	5	6	15 16	17	4	13 14	24	25	Р	и	и	21	22	23	26	28	6Д	р/с	б/с	2
1	1	1	—	4	5	3	2	4	4	—	1	2	1	—	—		1	2	1	2	2	—	1	1	1	7	7	1	55	22,0
т			1																							1	3	—	6	2,4
/	5	2	1	1	5	7	2	7	2	2	1	3	—	5	1		3	3	3	2	3	2	—	2	2	7	—	—	71	28,4
V	5	—	1	4	3	3	3	6	3	2	1	2	2	5	1	!	3	5	2	2	2	1	1	2	1	9	3	4	77	30,8
А	2	1	1	4	5	1	1	5	1	2	1	1	—	2	1	2	3	3	2	1	3	1	1	3	1	6	2	—	56	22,4
С	5	2	—	2	2	1	1	5	3	1	—	2	1	5	2	1	4	5	4	1	1	—	1	3	3	5	—	1	61	24,5
р	2	—	—	2	2	3	3	1	1	1	1	2	1	2	—	—	1	2	—		2	—	—	—	—	5	2	2	34	13,6
<2	3	1	—	2	3	1	3	4	1	2	3	2	1	3	—	2	4	3	3		2	—		2	—	6	7	3	61	24,5
р	3	1	—	2	2	2	2	5	2		—	2	1	3	—	1	1	1	—	1	1	—	—	—	—	6	2	2	40	16,0
и	3	—	—	—	1	—	1	—	—		—	2	1	3	—	—	—	1	—	1	—	—		—	—	2	—	1	16	6,4
2	29	8	4	21	28	22	18	37	17	10	8	18	В	28	5	7	20	26	15	10	16	4	4	13	8	54	26	14	476	190

Информативность, уел. ед. информации (УЕИ)

11, 6 3,2 1,6 8,4 11,2 8,8 7,2 14,8 6,8 4,0 3,2 7,2 3,2 11,2 2 2,8 8 10,4 6 4 6,4 1,6 1,6 5,2 3,2 21,6 10,4 5,6 190

Примечание: б/р — безразмерные величины,

р/с — размерные специфические величины, б/с — безразмерные специфические величины

■0.6

■0.6

Информативность, уел. ед.

‘0.4

‘1.0

"0.2

-1—— 1—— 1—— г

®ф©®ффф®®ф П АРАМЕТРЫ

Рис. 3.2. Информативность основных параметров ГТИ

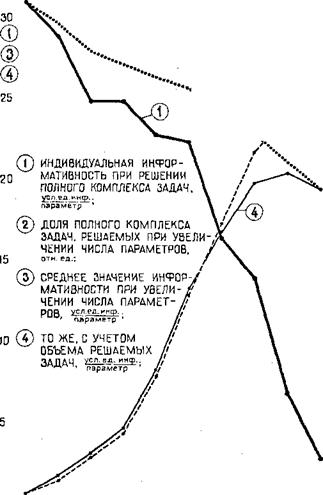
На рис. 3.2 (кривая 1) показана индивидуальная информатив­ность измеряемых параметров ГТИ (по степени падения инфор­мативности) при условии суммарного использования их в 4 из­мерительных комплексах. Наибольшей информативностью об­ладает параметр скорости (30,8 УЕИ), наименьшей — параметр времени (2,4 УЕИ).

Интересно проследить динамику роста объема решаемых за­дач с увеличением количества измеряемых параметров. При ус­ловии сохранения той же последовательности измеряемых пара­метров (V, /, (7, (2, Л, Ь, р, Р, V, 7) доля полного комплекса задач, решаемых при увеличении числа параметров, характеризуется кривой 2 на рис. 3.2.

Анализ этой зависимости показывает, что при последователь­ном наращивании 4 наиболее информативных измеряемых па­раметров (V, / <7, О) выполняется лишь 16% объема задач (-4% задач на параметр), последующее увеличение еще 4 менее ин­формативных параметров (А, Ь, р, Р) позволяет обеспечить 85% объема решаемых задач (-17% задач на параметр), последние два параметра (и, Т) снижают темп роста объема решаемых задач на 10 и 5%, соответственно.

Среднеарифметическое значение информативности одного па­раметра, определяемое как

(3.8)

где 11 — сумма информативности п параметров, изменя­

ется с ростом числа параметров по кривой 3 и достигает значения 19 УЕИ на параметр при полном наборе измеряемых параметров. Одна­ко кривая 3 построена без учета объема выпол­няемых задач и поэтому отражает истинную сред­нюю информативность лишь в последней точке (под 10-м параметром Т).

Динамика изменения истинной средней информативности на один параметр может быть определена по уравнению

(3.9)

2/ • Д УЕИ п параметр

где Д — доля полного объема решаемых задач, доля единицы. То же уравнение может быть представлено в виде

/сп = /с-Д.

Динамика изменения истинной средней информативности с учетом объема решаемых задач показана на рис. 3.2, кривая 4. Итоговое значение /сп совпадает со значением /с (19 УЕИ/пара — метр).

Таким образом, истинная средняя информативность изме­ряемых параметров ГТИ зависит от объема решаемых задач и может быть повышена до 20 УЕИ/параметр против 1 УЕИ/па — раметр, достигаемой при обычной регистрации измеряемых параметров ГТИ.

На рис. 3.3 показана оптимальная структура ИИС ГТИ и рас­пределение информационных потоков при проведении ГТИ. Здесь к измеряемым параметрам обязательного комплекса добавлены логические датчики состояния (ЛДС).

Логические датчики состояния не являются непосредствен­ными источниками информации, однако с их помощью стано­вится возможным получение служебно-сигнальной и производ­ной информации.

К ЛДС относятся: выключатель положения клиньев ротора, выключатель холостого хода талевого блока, выключатель нали­чия давления в гидравлической системе буровой установки, сиг­нализатор разъединения бурильных труб и т. п.

Информация от датчиков измерительных комплексов по­дается в блоки предварительной обработки (ПО), в функции которых входит первичная обработка измерительных сигналов (фильтрация, осреднение, интегрирование, нормирование и т. п.). После ПО информация поступает на средства отображе­ния информации (СОИ) 1-го уровня. Параллельно с этим ин­формация с блоков ПО подается в вычислительные контуры ВК1+ВК5, являющиеся составной частью управляющевычис — лительного комплекса (УВК). Информация, полученная в ВК, подается на СОИ 2-го уровня либо в следующий ВК. Все ВК связаны между собой межконтурным интерфейсом, позволяю­щим осуществить сквозную циркуляцию производной инфор­мации по всем вычислительным контурам. Интерфейс обяза­тельного комплекса связан со всеми ВК, интерфейсы допол­нительных комплексов связаны с ВК2+-ВК5. УВК в свою оче­редь имеет связь с СОИ 1-го уровня.

» — ^ фЫ • Ут»*1 ■■ ППГГ|1 —!ЧЬ

г *Л- 1 УВК

ОБЯЗАТЕЛЬНЫЙ КОМПЛЕКС (ОН)____

дкз

ДК2

ДК1

12     по

И по

по

75

59

15

-2- 1_

! КН

ВК4 ВК 5   1 т

вкз ~г

ВК2

ВК 1

т

СЛУЖЕБНО-Й=Н ПО сигнальная; инфорилция; —- -8-

-6-

■ЛДС

I 1________ УПРАВЛЯЮЩИЕ, Г" — .— —^ ВОЗДЕЙСТВИЯ

|_

ЛДС — логические датчики состояния ДК1 тдк з — дополнительные комплексы датчиков ПО — предварительная обРАБОтка ВК1 т ВК5 — вычислительные КОНТУРЫ

средства отображения информации (СОИ) 1и уровня | средства отображения иншормации(С(Ж)2иУРОВНЯ

-8- непосредственно определяемых] количество 59 вычисляемых параметров

интерфейсы СООТВЕТСТВУЮЩИХ комплексов

—— МеЖКОНТУРНЫЙ интерфейс

Рис. 3.3. Оптимальная структура ИИС ГТИ

СОИ представляют собой аналоговые и цифровые регистра­торы, плоттеры, принтеры, дисплеи, цифровые и звуковые ин­дикаторы, указатели, сигнальные лампы, табло и т. п.

Такая структура ИИС ГТИ является оптимальной, так как по­зволяет минимизировать набор технических средств, оптимизи­ровать процесс вычисления производной информации, рациональ­но распределив его по вычислительным контурам по параллель­но-последовательному принципу, иметь «горячее резервирование» В К, обеспечить сквозную циркуляцию получаемой информации и возможность ее представления на любых СОИ.

На рис. 3.4 показана информативность комплексов ГТИ в виде интегральной кривой роста информативности при последователь­ном наращивании измерительных комплексов и последователь­но-параллельной работе вычислительных контуров ВК1-^-ВК5. Сум­марная информативность ИИС ГТИ при решении вышеперечис­ленного объема задач может достигать 200 УЕИ.

Комментарии запрещены.