Спрощена система рівнянь
Спрощена система рівнянь
Побудовані системи рівнянь авторами [67, 212] досить складні. Отримаємо декілька спрощені рівняння, хоча при цьому втратимо деяку інформативність результатів. На початковій стадії вивчення проблеми важливо досліджувати достатньо прості випадки. З цією метою введемо коефіцієнти:
|
ka] lka4 кьі, |
(3.107) |
|
ka21 ka4 — kb2lkbi, |
(3.108) |
|
ka3ika4 — кьзікьь |
(3.109) |
|
ka4 — кь4ікьі, |
(3.110) |
|
ka5ika4 + l<bs 11<ь і ■ |
(3.111) |
Тоді рівняння функціонування мікроорганізмів запишуться у вигляді:
|
dmi/dt = kiinb |
mi(0) = тю, |
(3.112) |
|
dm2/dt = k2mb |
m2(0) = m20, |
(3.113) |
|
dm3/dt = k3mb |
m3(0) = m30, |
(3.114) |
|
dm4/d t= — кдтц, |
m4(0) = m4o, |
(3.115) |
|
dw/dt = k5mi + 6(Tn—’T)S, |
w(0) = w0, |
(3.116) |
|
w = c-rn-T. |
(3.117) |
Тут спрощення звелося до об’єднання доданків при подібних членах і позначення їх одним символом. У математичному відношенні тут немає якої-небудь зневаги членами. При цьому спрощується тільки структура системи, а сам процес розмноження і відмирання окремо не розглядаються, а об’єднані в один єдиний процес. Після заміни двох процесів одним, вже важко їх знову розділити на два процеси однозначно, якщо це буде потрібно. Об’єднання — од-
незначний процес, а розділення — не однозначний. Для отримання однозначного розділення треба знати структуру системи, долі кожного з цих процесів. Якщо до цієї проблеми підійти формально, то вона зводиться до того, що по відомих п’яти коефіцієнтах кь к2, к3, к4, к5 потрібно вирішити п’ять рівнянь (3.112)-(3.117) і визначити десять невідомих коефіцієнтів kail, ka2i, казі, к5Ь кЬ2Ь кьзь кЬ4Ь кЬ5Ь ка4, кы. По суті коефіцієнти кац, ка2Ь казь к5Ь кЬ2Ь кьзь кЬ4Ь кЬ5, визначаються структурою процесу. Залишаються невизначеними два коефіцієнта ка4, кы. Перший з них ка4 (або каі) визначається процесом розмноження, а другий кЬІ — відмирання. Отже між процесами є певні пропорції і при ідентифікації параметрів моделі треба користуватися ними.
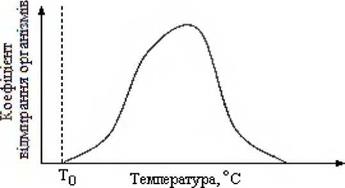
Для обчислення коефіцієнтів рівнянь використовуються приведені вище формули. Але у ряді випадків пропонується спрощена апроксимація їх квадратичною залежністю. Недолік їх в тому, що квадратична залежність не дозволяє враховувати асиметрію кривої щодо вертикальної осі. Тому менш точно апроксимують, чим формули (3.47)-(3.53) і (3.70)-(3.81), але зате значно простіше для аналізу. Крім того, ряд експериментальних даних дає залежність коефіцієнта від температури достатньо близьку симетричній. Наприклад, характерна експериментальна залежність [67, 70, 73, 74] приведена нарис. 3.10.
|
Рисунок 3.10 — Характерна експериментальна залежність |
На основі аналізу експериментальних [67, 70, 73, 74] коефіцієнт кі пропонується приблизно апроксимувати наступною залежністю:
k1 = k1(T) = k01 + kTIT-kT2T2, (3.118)
к, = к,(Т) = кот,(Т-То) — кот2(Т—То)2,
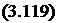
де зв’язок між коефіцієнтами апроксимацій (3.118) і (3.119) задається формулами:
де кп, кт2, кої, к0ть котг, Т0 — величини, які потрібно визначити при апроксимації експериментальної залежності коефіцієнта каі від температури.
Величина Т0 — температура, при якій припиняється життєдіяльність мікроорганізмів. Температура, зазвичай, вимірюється в градусах за шкалою Кельвіна. При Т>Т0 починається деяка життєдіяльність мікроорганізмів, якщо kj>0. Відмітимо, що член — кот2(Т—То)2 у формулі (3.119) негативного знаку. Він погіршує зростання популяції мікроорганізмів. Чинник впливу температури враховується коефіцієнтами к0ті і к0т2-