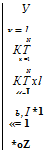Бурение грунтовых зондов, установка энергетических колодцев

Різні властивості використовують для описання математичних моделей. Поліноми алгебри знайшли найширше застосування. Розкладання невідомої функції в ряд Тейлора в околиці будь-якої точки з області її визначення

ч = ИЗД *«)=Я> + Х RX. + £ +1ДХ+-

L<j<h I4S*’ 1<*’-г ^ (7.107)

Апроксимуючи невідому функцію (хі, х2, …, хк) поліномом деякої міри обмежуються кінцевим числом його членів, але це тільки на практиці, а в загальному випадку степінний ряд нескінченний. Якщо функція відповідає ряду вимог, то подібна апроксимація має сенс. Безперервність і достатня «гладкість» є основними вимогами. Оскільки заздалегідь невідомо, наскільки ця вимога виконується, доводиться робити допущення про те, що це так.

Математичною моделлю можна представити відбиток газу в реакторі, та за лінійним рівнянням:

Я = *І>+5>Л

«*1

Де Ь0 — загальний ефект всього експерименту;

Ьі — ефекти чинників ;

Xj — чинники.

Будь-яку з поданий моделей можна вважати лінійною[77, 79, 90].

Поліном другої міри від к чинників:

y bQ + brt +b2x2+…+bkxk +bl2x x2 +bl, xlx3 +b21x2 + …+bkixk

Якщо ввести фіктивну змінну Хо = 1 і провести заміну нелінійних членів таким чином:

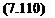ХХ2 ~ -‘•А+1>Х1Х! Xk+29"’*Xk-lXk ~ Хклі{ ’

(7.111)

(С2К — число поєднань з k по 2), то отримаємо однорідне лінійне рівняння [75,103].

(7.112)

Дані моделі завжди лінійні по невідомих коефіцієнтах, нелінійними можуть бути по чинниках.

Зображений на рис. 7.25 метод найменших квадратів зазвичай використовують для обчислення коефіцієнтів моделі. Спроможність, несмещенність, ефективність і достатність — оптимальні властивості в статистичному сенсі. При збільшенні об’єму вибірки оцінка коефіцієнта приближається до істинного значення коефіцієнта; Якщо математична оцінка коефіцієнта рівна оцінюваному значенню, то вона вважається незміщенною; ефективною вважають, якщо оцінка характеризується мінімальною дисперсією, а достатньою, коли включає максимум інформації про коефіцієнт.

Наступна функція відображає і мінімізує метод найменших квадратів:

(7.113)

де у„ і У u — відповідно експериментальні дані і розраховані по рівнянню (7.112) значення у у ц — му досліді; N — загальна кількість дослідів.

Введемо фіктивну змінну хо, що набуває в усіх дослідах значення

Мінімум функції (7.113) знаходимо прирівнюванням нулю масних похідних:

(7.114)

Система нормальних рівнянь методу найменших квадратів:

Л

= І.

*=І

Л

= І

її > 1

у

= Z х«.г»

н = »

Невідомі коефіцієнти моделі знаходимо в результаті вирішення системи. Кожен коефіцієнт вирішується за власним рівнянням:

Zv. ЇХ*.

*4 = =%-т-Л =-=^-3-. (7-116)

Z— Z-< Zx2. Z Zx<.

(7.117)

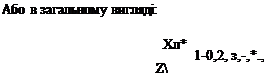Як висновок треба зазначити:

> Внесена наукова передумова об’єднання трьох стадій в єдиний цикл анаеробного зброджування відходів тварин і птахів;

> Щоб пояснити процеси, шо відбуваються під час утилізації відходів тварин і птахів, запропоновано застосовувати механізми акумуляції і енергію при анаеробному зброджуванні посліду;

> Запропоновано використовувати модель графа мережі Петрі у структурній оптимізації технологічного процесу зброджування посліду;

> запропонована математична модель оптимізації процесу утилізації відходів тварин та птахів.

1.

Комментарии запрещены.