Аналіз деяких окремих випадків
Аналіз деяких окремих випадків
Варінт 1. Розглянемо випадок, коли в моделі на розмноження мікроорганізмів не враховується вплив газів, що утворяться, і інших продуктів їхньої життєдіяльності. Наприклад, гази безупинно віддаляються, та інші продукти життєдіяльності мікроорганізмів з’їдаються іншими мікроорганізмами або змиваються, а живильних речовин для перших мікроорганізмів досить. Тоді з огляду на формулу (3.130) для визначення коефіцієнта
кі = кі(Т) = к0і + кцТ — кцТ2, модель процесу запишемо у вигляді:
(dmi/dt)/ mi= кю + кцТ — к2Т2, ті (0)=тю, dcmT/dt=k5 т, б (Тп-Т), Т(0) =Т0,
де кю, кть кт2, т ю, с, к5, Тп, Т(| задані постійні величини.
Був зроблений чисельний аналіз цієї системи, розглянуто шість випадків. Значення коефіцієнтів обрані з таблиць по їх фізичному змісту, так щоб модель якісно відображала реальний процес. Спочатку розглянемо наступні три варіанти (рис. 3.12 та рис. 3.13):
1)к10 = -2-1(Г3(годч), кт,= юДк-‘тодЛк-^ 1,515-1(Г8(ІС2тодч), к5= 8 (кДж/(кг-год)), 6 = 2 (МДж/(К-год)), с = 4000 (Дж/(кг-К)),
m = 1000 (кг), нію= 300 (кг), Тп= 280 (К), Т0= 300 (К).
2)кю — —2’10 3 (год 3), kTi ~ ІоДіС’тодДк-і^ ^ІЗ-юДк^-год4), к5 = 8 (кДж/(кг-год)), 6 = 2 (МДж/(К-год)), с = 4000 (Дж/(кг-К)),
m = 1000 (кг), іню= 300 (кг), Тп= 280 (К), Т0= 270 (К) (переохолоджене органічне середовище).
3)к10 = -2-1(Г3(годч), кт1= КГ5(Кчтод-‘),кт2 = 1,515-1(Г8(ІС2тодч), к5 = 8 (кДж/(кг-год)), 6 = 2 (МДж/(К-год)), с = 4000 (Дж/(кг-К)),
m = 1000 (кг), іню= 300 (кг), Тп= 280 (К), Т0= 360 (К)
(перегріте органічне середовище).
|
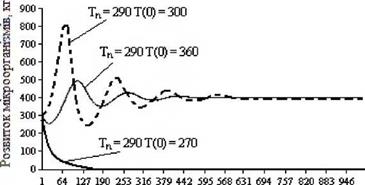
Температура, К Рисунок 3.12 — Залежність розвитку мікроорганізмів від температури |
|
Рисунок 3.13 — Залежність розвитку мікроорганізмів від температури |
У першому випадку температура органічного середовища сприятлива для росту мікроорганізмів, у другому ж і в третьому вона згубна для них.
Це видно і на графіку — у другому випадку маса мікроорганізмів швидко убуває і, через якийсь час, вони зникають повністю.
У третьому ж випадку їхня маса спочатку теж убуває, але вміст контейнера встигає остудитися до прийнятної температури і починається ріст мікроорганізмів.
У першому випадку ріст маси мікроорганізмів спостерігається із самого початку. Але в міру росту вони починають виділяти, у процесі життєдіяльності, тепла більше чим приділяється через стінки контейнера. Таким чином, у якийсь момент маса перегрівається і
починається загибель мікроорганізмів. Поступово маса прохолоджується до температури сприятливої для росту мікроорганізмів і знову починається їхній ріст.
Таким чином, у першому і третьому випадках процес поступово сходиться до деякого стаціонарного, для даної системи, режиму.
Тепер розглянемо наступні три варіанти (рис. 3.14 та рис. 3.15):
4) кю = -2-1(Г3(годч), кт,= юДк^тодЛк^ 1,515-1(Г8(ІС2тодч), к5= 8 (кДж/(кг-год)), 6 = 2 (МДж/(К-год)), с = 4000 (Дж/(кг — К)), т= 1000 (кг), пцо= 300 (кг), Тп= 300 (К), Т0= 290 (К).
5) кю = -2-1(Г3(годч), кт1= КГ5(Кчтод-‘), kта= ЮН-юДк^тодД, к5 = 8 (кДж/(кг-год)), 6 = 2 (МДж/(К-год)), с = 4000 (Дж/(кг-К)), m = 1000 (кг), тю = 300 (кг), Тп= 270 (К), Т0= 290 (К) (переохолоджене органічне середовище).
6) кю = -2* 10-3(год_1), кТі = 10“5(К“‘*год-1), кт2= иіЗ’ІОДісЧод-1), к5 = 8 (кДж/(кг-год)), 6 = 2 (МДж/(К-год)), с = 4000 (Дж/(кг-К)),
m = 1000 (кг), пцо = 300 (кг), Тп= 360 (К), Т0 = 290 (К)
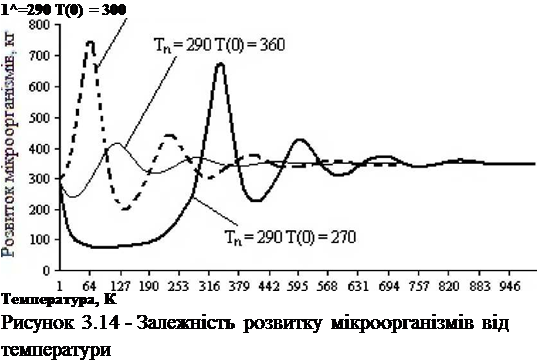 |
(перегріте органічне середовище).
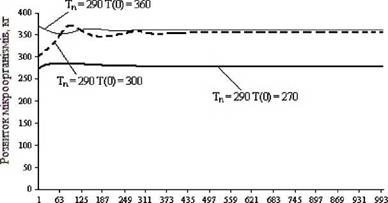
Рисунок 3.15 — Залежність розвитку мікроорганізмів від температури
У цих трьох випадках ситуація в цілому аналогічна розглянутим раніше. Тільки в п’ятому випадку, завдяки більшій температурі зовнішнього середовища, споконвічно переохолоджене органічне середовище встигає нагрітися, до сприятливої температури, перше ніж всі мікроорганізми загинуть, і їхня популяція поступово сходиться до стаціонарного значення, як і в четвертому і шостому випадках.
Варіант 2. Припустимо, що коефіцієнт теплоємності постійний і дуже малий. Температура швидко встановлюється, і перехідним процесом зневажаємо, тобто dcmT/dt=cdm/dt=0. При цьому Т=Тп+к5Гїіі/6. Досліджуємо вплив температури зовнішнього середовища Тп на розмноження мікроорганізмів. При цьому:
(dmi/dt)/mi=a+bmi-cmi, ті(0)=тю, (3.140)
де а=кіо+ктіТп-кТ2Тп2, Ь=(кті-2кт2Тп)к5/8, с=кт2(к5/8)2.
Введемо функцію y=a+bm1-cm12. При a+bm1-cm12=0 рівняння
(2.120) має два стаціонарних рішення:
ші(1) = Ь/2с + ((Ь/2с)2 + а/с)172 = const,
mi(2) = Ь/2с — ((Ь/2с)2 + а/с)172 = const.
При а>0, Ь>0, с>0 друге рішення стає негативним і тому з розгляду виключається. Залишається єдине рішення m/1)=const. Якщо в околиці цього рішення давати невеликі збурювання в меншу або в більшу сторону, то одержимо, що при величина у стає по-
зитивною і, відповідно до рівняння (3.140), dm|/dt — також позитивною. Тоді ні] зростає і наближається до стаціонарного рішення. Якщо ж то одержимо у<0 і dmj/dt<0. При цьому значення
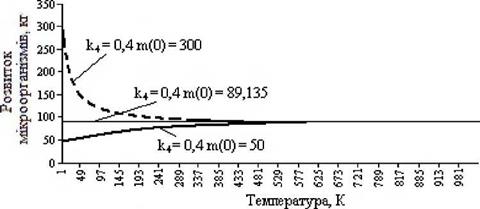
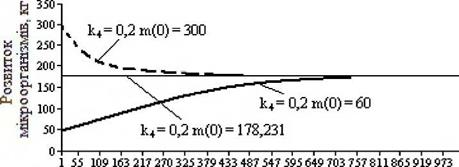
ні! убуває. Отже, вертається до стаціонарного значення т/Ч Це ознака того, що стаціонарне рішення стійке. Що й було підтверджено на декількох прикладах (рис. 3.16 і рис. 3.17) чисельним аналізом. Розглянемо приватні значення коефіцієнтів:
1) к10 = -0,01 (год”1), кТ1 = 2 -10-[2] [3] (К^тод-1) кТ2 = 3,279-10”[4] (К^-год"1), б = 0,2 (МДж/(К/год)), Тп= 300 (К), к5= 8 (кДж/(кг/год)),
тю = 300 (кг).
2) к,0 = -0,01 (год[5]), кт1 = 2- КГ5(К4-год4), кта = 3,279-КГ7(К-2тод-‘), б = 0,2 (МДж/(К/год)), Тп= 300 (К), к5 = 8 (кДж/(кг/год)),
тю = 50 (кг).
3) к,0 = -0,01 (год4), кт, = 2-Ю-^К-‘тод-‘), km = 3,279-КГ7(К-2тод-‘), б = 0,2 (МДж/(К/год)), Тп= 300 (К), к5= 8 (кДж/(кг/год)),
m10= 178,23 (кг).
|
Рисунок 3.16 — Залежність розвитку мікроорганізмів від температури |
|
Температура, К Рисунок 3.17 — Залежність розвитку мікроорганізмів від температури |
Варіант 3. Проаналізуємо розвиток мікроорганізмів під впливом зовнішнього нагрівання. Приймемо, що c=const і pH=const, а отруйні речовини не виділяються Тоді процес описується системою (3.21)-(3.25) і з них розглянемо два рівняння:
dm1/dt = k1m1, m1(0) = m10, (3.141)
dT/dt = (1 /cm)k5іп і + (6/cm)(Tn — T)S, T(0) = T00. (3.142)
Інші рівняння служать для визначення кількості газів т2, інших продуктів життєдіяльності мікроорганізмів т3 і витрачених живильних речовин т4. При прийнятих умовах вони на процес не впливають і визначаються після рішення розглянутої системи двох основних рівнянь. Коефіцієнти кі і к5 визначаються по формулах:
кі = каі — кьь
к 5 = ка5 + кь5,
а коефіцієнти ка5 і кь5, які входять у ці співвідношення, представляються вираженнями:
1<а5 ka5i(l/kaii)kai,
kb5 = кь5ікьі,
де ка5і, каі і, кь5і — постійні величини, обумовлені структурою процесу.
Коефіцієнти каі кы апроксимуємо спрощеними формулами:
каі = коті(Т-То) — к0т2(Т-Т0)2, кы = кьті(Т-Т0),
Тоді коефіцієнти к| і к5 запишуться у вигляді:
ki = (кои _ кьті)(Т-Т0) — к0т2(Т-Т0)2,
к 5 = [(ка5і/кц)коті + кь5і + кьц](Т-То) — (ка5і/кц)кот2(Т-То)2.
Уведемо позначення:
І! 11 = (коті — кьті), І1|2 = к0Т2,
ІІ21 = (ка5і/сітік| і)к()ті + кьті/(с-т),
ІІ22 = (ка5|/стк| і)к0Т2, h23 = S/(c-m),
ТОДІ
кі = 1іц(Т-Т0) — 1і!2(Т-Т0)2,
к5 = cm[h21(T-To) — ЬгаСТ-ТоЛ].
Використовуючи ці позначення і коефіцієнти к| і к5, рівняння
(2.121) і (2.122) запишемо у вигляді:
dnn/dt = [Ііц(Т-То) — 1іі2(Т-То)2]ті т^О) = т10, (3.143)
dT/dt = [І121(Т-Т0) — ІІ22 (Т-Т„)2,] m, + h23(T„-T), Т(0) = Т(ю, (3.144)
Проаналізуємо цю систему. Якщо початкове значення температури Т0о нижче, ніж Т0, то в цих умовах мікроорганізми не можуть розвиватися і варто прийняти кх=0 и m1(0)=0. Якщо і є мікроорганізми, то процесу їхнього розмноження не відбувається. Тоді залишається тільки останнє рівняння, що записується у вигляді:
dT/dt = h21(Tn-T), Т(0) = Too.
За рахунок нагрівання від зовнішнього середовища, тобто температури Тп якщо вона не нижче Т0, органічне середовище з мікроорганізмами буде розігріватися до температури Т0, після якої мікроорганізми почнуть оживлятися, і самі будуть виробляти теплову енергію. При цьому температура може і перевищувати Тп. З огляду на це надалі початкову температуру Т(0) приймемо рівною Т0 або вище Т0.
Помітимо, що коефіцієнт hn може бути і негативного знака, якщо коті<кьті тобто в одиницю часу гинуть більше мікроорганізмів, чим народжуються. При цьому популяція мікроорганізмів може тільки зменшуватися. Найцікавіший випадок, коли hi і позитивного знака, при якому популяція може, як розвиватися, так і убувати залежно від свого стану, у цьому випадку від температури середовища.
Перше рівняння (3.22) з роздільними змінними. Воно розв’язується відносно пі!:
иіі = пік, ехр Ц[1іцТ — Т0) — 1тг2(т — T0)2]ds|. (2.125) (3.145)
Підставляючи ті у друге рівняння, одержимо диференціальне рівняння для температури:
^ = [h21(T-T0)-MT-T0)?]-m10x
dt. (3.146)
xexp{J[h11T-T0)-h12(T-T0)2]ds} + h23(T11 — Т), Т(0) = Т„„
Це нелінійне рівняння і аналітично не вирішується. Рішення його проаналізуємо чисельним методом при різних значеннях параметрів рівняння. Помітимо, що при t=0, Т(0)=Т()„. одержимо (dT/dt)t=o=h23(Tn-Too). При (Тп-Т)>0 відбувається поступове нагрівання поки не досягне максимального значення, що відбудеться при dT/dt=0, а далі температура починає убувати.
Спочатку чисельно вирішуючи диференціальне рівняння (3.146), визначається розподіл температури, потім отримані значення температури підставляються у формулу (3.145) для визначення розвитку маси популяції мікроорганізмів і будується закон розвитку популяції. Далі, використовуючи їх, визначається кількість виділюваних газів в одиницю часу і споживання живильних речовин.