Бурение грунтовых зондов, установка энергетических колодцев

6.2.3.1. Теоретичні основи ди&ракиійного Memodv

Суть дифракційного методу формування опорного напряму базується на фізичних явищах дифракції світла на отворах різної форми. В основу метода покладається схема відомого досліду Юнга, де діафрагма (щілина) джерела світла, вісь симетрії щілин проміж­ного екрану і вісь ахроматичної полоси дифракційної картини в площині спостереження завжди знаходяться в одній площині. Спостерігач при розгляді дифракційної картини, на­приклад через зорову трубу, побачить характерні для неї дифракційний максимум в центрі і симетрично розташовані дифракційні спектри по обидва боки від нього.

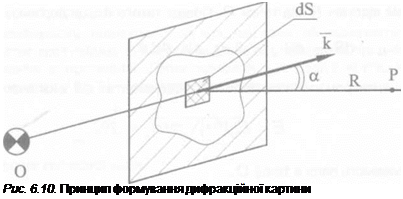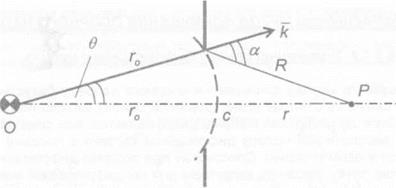
Результат взаємодії світлового потоку з отвором довільної форми на проміжному ек­рані приведено на рис. 6.10.

Світлове поле в довільній точці спостереження Р знаходиться в відповідності з принципом Гюйгенса-Френеля [49], який говорить, що повне світлове поле є результатом інтерференції вторинних хвиль від елементів отвору dS, тобто має місце складання ам­плітуд коливань, створених діючими ділянками фронту падаючої хвилі. Величина напру­женості поля в точці Р записується виразом

iikR

Ер = к(а) Е — dS, (6.9)

S

де: к(а) — деякий коефіцієнт, який враховує залежність амплітуди вторинних

хвиль від кута а між вектором к і напрямом на точку спостереження; к — хвильове число.

Модуль к(а) максимальний при а = 0 і зменшується при збільшенні а.

Топографія зон Френеля залежить від форми прозорих і непрозорих зон і від поло­ження екрану відносно джерела світла (точка О) і площини спостереження (точка Р). Прозорі і непрозорі зони можуть бути нанесені у вигляді вертикальних, горизонтальних або перехрещених під прямим кутом смуг, а також у вигляді концентричних кілець. Для спрощення задачі обмежимось симетричним круглим отвором і знайдемо розподіл напру­женості поля в точці Р, яка лежить на осі, що з’єднує джерело світла і центр круглого от­вору (рис. 6.11).

Рис. 6.11. До визначення напруженості поля в точці спостереження

В якості елемента dS в цьому випадку зручно взяти кільце на сфері всі точки якого лежать на однаковій відстані R від точки Р. Площа такого кільця дорівнює

dS = dS п = 2nr0 sin 6d6. (6.10)

Напруженість електромагнітного поля на всіх елементах dS визначається виразом

Е = Е0Іікг°, (6.11)

де Е0 — напруженість поля в точці О.

За змінну інтегрування в (6.9) слід вибрати R, тобто необхідно врахувати, що точка Р може знаходитись на різних відстанях від екрану. Із рис. 6.11 маємо

де: r0 — відстань від точки О до сфери;

г — відстань від сфери до точки Р.

Прийнявши значення г0 і г постійними величинами після диференціювання рівнян­ня (6.12) по в отримаємо

RdR = г0 (г0 + r)sin всів, (6.13)

З урахуванням (6.13) вираз (6.10) запишемо у вигляді

dS„=2x-r°?-dR. (6.14)

Г0+Г

Підставляючи (6.11) і (6.14) в (6.9) отримаємо напруженість поля в точці Р

у ^max

Ер — 2л E0likr° jk(R)likRdR. (6.15)

0 ‘ • г„

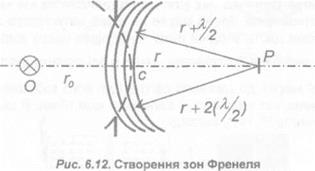
Для наближеного результату обчислення інтеграла (6.15) користуються прийомом, який полягає в тому що будують сфери з центром в точці Р, радіуси яких дорівнюють

г, г + У2,г + 2(л/2), г + п(У2) (рис. 6.12).

Ці сфери розбивають поверхню S на кільцеві зони, які називаються зонами Френе­ля. Із побудови стає зрозумілим, що вторинні хвилі від межі двох сусідніх зон приходять в точку спостереження в протифазі. Легко показати, що радіус круга, який відокремлює п — ну зону Френеля від (п + 1) — ї зони приблизно дорівнює

Rn=^n? irr0/{r + r0), (6.16)

де Я — довжина світлової хвилі.

Із (6.16) видно, що площі зон Френеля приблизно однакові. Так як X < г, то зміна R в межах однієї зони не значна і плавну функцію k(R) в підінтегральному виразі (6.15) при інтегруванні по п — ній зоні можна рахувати постійною. В цих наближеннях вклад п — ої зо­ни в інтеграл легко обчислюється за формулою

Г+П¥г 2к

кп | eikrdR = (-l)n neikr,

ik

де кп — значення функції k(R) в межах /7-ої зони. Обчислення напруженості поля в точці Р зводиться до підсумовування знакоперемінного ряду

Ер = (4*іг0Е0 /кУ^%-к2+к3-к4 +…). (6.18)

Аналіз виразу (6.18) дозволяє зробити вельми важливий висновок для використання зон Френеля при формуванні референтної лінії. При збільшенні отвору в екрані освітле­ність в точці Р змінюється не монотонно: поки відкривається перша зона Френеля освіт­леність збільшується і досягає максимуму при повністю відкритій зоні; при подальшому збільшенні діаметра отвору — по мірі відкривання другої зони Френеля — освітленість змен­шується і при повністю відкритих двох зонах мчиться майже до нуля. Потім при збільшенні діаметра отвору відкривається третя зона і освітленість знову збільшується і так далі. Та­ким чином, якщо відкриті всі непарні зони Френеля (1,3,5…) інтенсивність освітлення в

точці Р можна суттєво підсилити, так як вторинні хвилі від всіх відкритих зон Френеля бу­дуть приходити в точку спостереження в однаковій фазі і в результаті інтерференції підси­лять одна другу. Екран з відкритими непарними зонами Френеля називається зонною мар­кою (пластиною) або лінзою Френеля.

Аналогічно можна виготовити екран з відкритими парними зонами Френеля. Дія кож­ної зонної марки описується рівнянням (6.18), якщо в ньому залишені члени одного знаку. Зонна марка, яка містить п відкритих зон, створює в точці Р освітленість приблизно в п2 разів більшу, чим отвір в одну зону Френеля. Зонна марка створює зображення подібне до створеного лінзою або сферичним дзеркалом. Ідеальна лінза перетворює плоску хвилю в сферичну, центр кривизни якої знаходиться в центрі лінзи. Лінза створює такі різниці фаз, які необхідні, щоб вторинні хвилі від цих ділянок падаючого на неї хвильового фронту зби­ралися в фокусі в однаковій фазі. Зонна марка не може дати такого доброго ефекту, так як не всі ділянки кожної зони діють в одній фазі. Внаслідок цього амплітуда від всієї зони в

2/ — разів менша тієї, яка була б отримана, якщо б всі ділянки діяли синфазно.

Відстані від зонної марки до джерела світла і до його зображення в точці Р зв’язані таким же співвідношенням, що і відповідні величини для лінзи. В цьому легко пересвідчи­тись, переписавши формулу (6.16) у вигляді

1	1	1
1 + 1	~ Ґ	(6.19)
1	пЯ	Я
f R2n	2’	(6.20)

де f — фокусна відстань — постійна величина для даної зонної марки, так як права частина (6.20) не залежить від п (Pn » Vn). На відміну від лінзи зонна марка має декілька фокусів. Дійсно, наблизивши точку спостереження до марки, можна знайти таке її поло­ження, коли в центральному світлому крузі марки вміститься три перших зони Френеля (а не одна). Наступні три зони будуть перекриті темним кільцем. Потім три зони будуть збіга­тись із світлим кільцем і т. д. Радіуси зон Френеля визначаються формулою (6.16) для пер­шої зони

Ri =Угг0І(г0+г) = 4м,

де f визначається виразом (6.19). Якщо г = г0, тобто екран розташований посере­дині між джерелом і точкою спостереження, то f = —. При дифракції плоскої хвилі, коли

використовується, наприклад лазер, можна рахувати, що джерело знаходиться від екрана на нескінченності, тобто г0 -» од. Тоді f = г.

Розрахунок геодезичних зонних марок виконується по формулах, які дещо відрізня­ються від класичних для зонних пластин Френеля, що приводить до більш щільного розта­шування зон і наявності додаткової центральної смуги нульового порядку. Положення про­зорих і непрозорих зон Френеля визначається за формулами

go=Uror/2L)1/W.450;

qn={Ar0r/2L)144n-1.797)12; (6.22)

^п={Лгог/2ф(4п + 0.203)12,

де: с-.с-.с — — відповідно відстані від осі симетрії зонної марки до центральної зо­

ни, внутрішньої і зовнішньої сторони п — ої зони (рис. 6.13);

L = {r0 + г) — довжина референтної лінії.

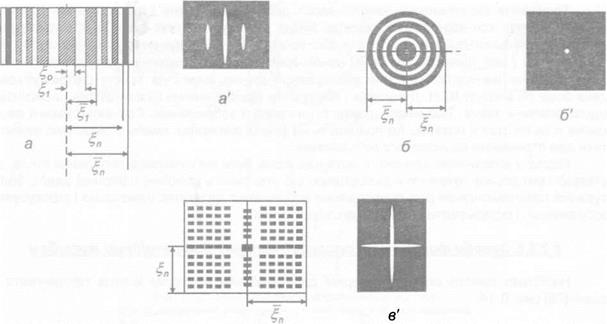
По формулах (6.22) розраховують всі типи зонних марок: одномірну (рис. 6.13 а), двомірну (рис. 6.13 в), кругову (рис. 6.13 б) та деякі інші. В теперішній час найбільшого розповсюдження отримали одномірна і двомірна зонні марки.

в Рис. 6.13. Геодезичні зонні марки і їх зображення: а — одномірна; б — кругова; в — двомірна.

Одномірна геодезична зонна марка з прямолінійними зонами (рис. 6.13 а) формує в точці спостереження зображення у вигляді вузької вертикальної світлової смуги шириною d. Розрахунок ширини d зображення, яке формується якісно виготовленою зонною мар­кою, може бути виконаний за формулою

де D = — відстань між крайніми зонами реальної марки, тобто ефективна ширина

робочої зони. Її можна підрахувати за формулою [49]

де N — 2п — необхідне загальне число всіх прозорих зон марки.

Так при п — 25(N — 50), r ~r0 -100м, Л = 0,6328 мкм, D = 78 мм, d -0.6 мм. При виготовленні зонних марок загальну кількість прозорих зон обмежують величиною 2п < 50, так як наступне збільшення їх числа мало впливає на ширину зображення, яке формується однорідною зонною маркою.

Двомірна зонна марка із перехрещених прозорих і непрозорих періодичних структур щілин (рис. 6.13 в) формує зображення системи смуг у вигляді хреста, центр якого розта­шований на одній осі з оптичною віссю джерела випромінювання і центром зонної марки. Зонна марка з круговими зонами (рис. 6.13 б) формує дифракційне зображення у вигляді яскравої світлової точки малих розмірів. Таким чином, для формування опорного напряму використовується властивість зонної марки формувати яскраве світлове зображення ви­значеної конфігурації, в залежності від виду зон на марці, строго симетрично відносно пря­мої, яка з’єднує джерело випромінювання і вісь симетрії зонної марки.

Технологія виготовлення зонних марок добре розроблена і полягає в нанесенні на екран прозорих зон відносно осі симетрії марки фотомеханічним шляхом або гравіруван­ням на спеціальних підкладках із скла або оргскла. На сьогодні методами фотолітографії можливо на 1 мм нанести до 2 000 ліній. Найбільш точно зонні марки виготовляються голографічним методом. Можливо записування зонних марок на товсту фотоемульсію з двох боків по методу Ю. Н. Денисюка і наступним відновленням білим світлом з селекцією однієї довжини хвилі. Такі марки дають тільки дійсне зображення. При записуванні зонної марки в світлі трьох лазерів, які працюють на різних довжинах хвиль, її можливо викорис­тати доя отримання кольорового зображення.

Поряд з класичною зонною пластиною може бути виготовлена голограма-лінза, яка створюється двома точечними джерелами, що утворюють розбіжні сферичні хвилі. Засто­сування голограми-лінзи для фокусування зображення дозволяє одночасно і сфокусувати зображення, і сформувати опорний світловий пучок.

6.2.3.2.
Засоби tboDмvвaння опооного напояmv дисЬоакиійним методом

За джерелом випромінювання 1, наприклад, лазером і однощільовою діафрагмою 2 розташовують соосно зонну марку 3 з перемінними відстанями між зонами. При випромі­нюванні лазера лінійна зонна марка, центральна зона якої має, наприклад, прозору зону шириною в два рази більшу чим сусідні, діючи аналогічно циліндричній лінзі, створює в площині фотоприймача 4 яскраве і різке зображення однощільової діафрагми. Застосу­вання лазера замість теплового джерела випромінювання підвищує контрастність зобра­ження. Використовуючи конструкцію фотоприймача доповнену бісектором, з’являється можливість підвищити точність визначення зміщення центра інтерференційної картини і розширити дію пристрою формування референтного напряму.

Формування референтного напряму в двох взаємно ортогональних площинах або в двох площинах, які перехрещуються під довільним наперед заданим кутом можливо за допомогою спектральної зонної марки спеціальної конструкції [147] рис. 6.15.

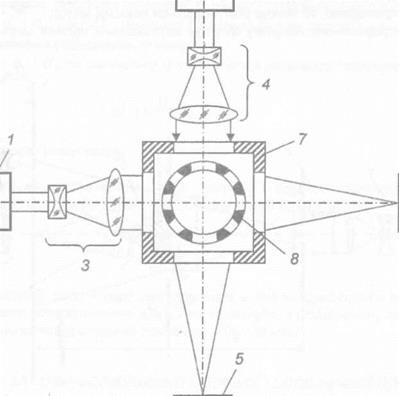
Рис. 6.15. Застосування дифракційного методу для формування референтного напряму у двох площинах

Референтні напрями формуються двома лазерами 1 і 2, які доповнені коліматора­ми З і 4 . Вимірювальна система постачається двома фотоприймальними пристроями 5 і б, розташованими в кінці напрямів. Кожний фотоприймальний пристрій оптично зв’яза­ний з відповідним лазером через одну спектральну зонну марку спеціальної конструкції 7. Марка містить корпус, в якому розташований дифракційний елемент 8. Останній викону­ють у вигляді циліндра, бокова поверхня якого має прозорі і непрозорі зони, при чергуван­ні яких діаметрально протилежні зони повинні бути рівними. Дифракційний елемент має можливість обертання навкруги вертикальної осі.

Перший референтний напрям формується, наприклад, лазером 1 при фіксованому нульовому положенні дифракційного елемента по фотоприймальному пристрою 6. Після цього дифракційний елемент обертається в корпусі на заданий кут. Розкручуванням лазе­ра 2 і фотоприймального пристрою 5 фіксується положення другого референтного нап­ряму.

Комментарии запрещены.