Бурение грунтовых зондов, установка энергетических колодцев

Точність поляризаційного методу залежить не тільки від чутливості приладу, але і від просторового положення основних оптичних елементів схеми — поляризаційних призм і пластини модулятора Фарадея. Оцінка указаної залежності необхідна для визначення до­пусків на установлення елементів приладу при його проектуванні, монтажі і в процесі екс­плуатації.

Нижче проаналізуємо вплив похибок просторового положення оптичних елементів поляризаційного пристрою на точність визначення кута скручування. В якості прикладу візьмемо схему із двох поляризаційних призм Глана і магнітооптичного модулятора Фара­дея з пластиною із кварцового скла. Одна із призм є поляризатором, друга — аналізатором, робочими частинами призм, що визначають положення площини коливань поляризовано­го світлового променя (для призм із ісландського штату — це І — промінь), будуть полови­ни, повернені одна до другої [50]. Точне рішення, що описує амплітудні відношення для різних світлових хвиль, які створюються на межі кристал — ізотропне середовище і ізотроп­не середовище — кристал, дається в роботі [175]. Вектор напруженості електричного поля світлової хвилі після проходження поляризаційної призми визначається виразом:

Е — Аа +В[па

де: А = (т]є0 — г}0ас)

В = -{г/ — г)0 і0 (Ь с) + а2 (qc) ;

є0 = п2 — діелектрична проникливість кристала для звичайного променя;

с — вектор оптичної осі кристала;- q — нормаль до вихідної поверхні призми; п — вектор рефракції вихідної із призми хвилі;

7 =- а2; ij0 = — yjs0 — а2 ; a = [nq] Ь =[qa].

Вираз (5.19) визначає поле поляризації в межах апертурного кута поляризатора.

Розглядаючи проходження світлової хвилі через пластину модулятора Фарадея, враховуємо, що в приладі модулятор звично жорстко скріплений або с поляризатором, або з аналізатором; при цьому пластина може бути точно орієнтована відносно робочої поверхні поляризаційної призми. Якщо модулятор розташований в блоці з поляризатором і пластина зорієнтована відносно його вихідної грані, то, використовуючи формули Френе­ля, для вектора напруженості електричного поля світлової хвилі після проходження плас­тини модулятора, отримаємо:

juE’ = A cos2(q>1 — ср)а + В[па (5.20)

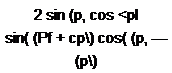% — кут падіння світла; cp — кут заломлення.

В процесі вимірювань аналізатор розкручують і приводять в погоджене положення з поляризатором, при якому на фотоприймач попадає мінімальний сигнал. Так як звичайний промінь поглинається в першій половині призми аналізатора, то умовою схрещеного поло­ження буде рівність нулю інтенсивності незвичайного променя в першій половині призми аналізатора, тобто:

)(є0а1 +а0 ) + В1(а0 + a1){a2(sc1)-a0s[a1c1]} = 0, (5.21)

де: a, =(ns) а0=^є0-а2 a, = [ns];

с1 — вектор оптичної осі кристала аналізатора; s — нормаль до вихідної поверхні аналізатора;

В1А1 — складові вектора Е" (відповідно паралельна і перпендикулярна до пло­щини падіння світлової хвилі на аналізатор).

/ІЕ" = А1а1 + В,[а п] (5.22)

Зв’язок між А, В,, і А, В можна знайти після почергового помноження (5.20) і (5.22) скалярно на а, і на [а, л]:

A =Acos2(<p1 — <р )(аа1 ) + Bfa^an]);

, _г_ , __ (5.23)

в, =Acos2(<p1-<p’1)(a[a1n)-B(aa1).

Підставляючи (5.23) в (5.21), отримаємо рівняння, яке визначає положення поляри­заційних призм при установленні їх в погоджене положення:

{д cos2 ({р1-(р1)(аа1) + В(а [а] її ]jVa, c,)(є0а, + а0) +

(5 24)

+ Acos2((p1-<p’1)(a [а. п]) — Bfaa,;})a2 (sc,) — a0s [а, с. ]} = 0.

Для вирішення рівняння (5.24) систему координат розташуємо таким чином, щоб вісь OZ збігалася з віссю пучка променів світла (рис 5.6). Нехай в початковому положенні по­ляризатор установлений так, що нормаль до його вихідної поверхні паралельна осі OZ, а оптична вісь кристалу лежить в площині YOZ. Кут між оптичною віссю поляризатора і ви­хідною поверхнею дорівнює у1. Відносно цього положення повернемо поляризатор на кут (р^ навкруги осі, яка складає кут а1 з віссю ОХ. Оптична вісь кристалу аналізатора нехай розташована під кутом у2 відносно його вхідної поверхні. При цьому нехай аналізатор бу­де нахилений на кут (рг навкруги осі, яка складає з віссю ОХ кут а2, і зміщений в площи­ні XOY таким чином, що світловий промінь, який проходить через призми, складає кут у/ з віссю OZ, а його проекція на площину ХОУ визначається кутом в з віссю ОУ. Нага­даємо, що установлення призм в погоджене положення здійснюється розкручуванням аналізатора навкруги осі OZ.

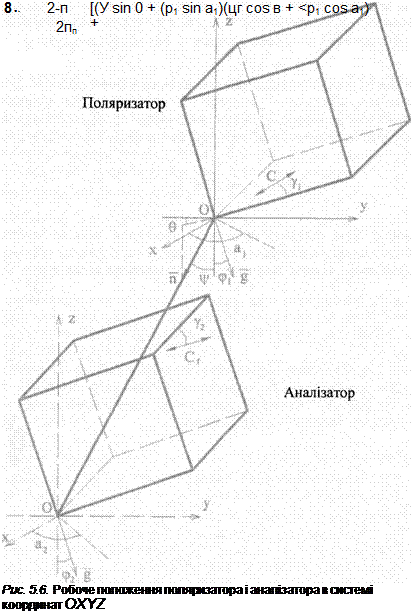В якості шуканого невідомого приймемо відмінний від 90° кут між осями призм, тоб­то кут між оптичною віссю поляризатора і нормаллю до поверхні, яка проходить через вісь аналізатора і нормаль до його вхідної грані. Позначимо ідей кут 8. З урахуванням малих значень кутів уи у2, <р1, (р2 і ц/, після обчислень, із рівняння (5.24) отримаємо:

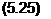+ (ур2 sin а2+у/ sin в) (у/ cos 9+ ср2 cos а2 j] — -y1(t//sin9 + <р, sinа1)-у2(у/cos6 + q>2 cosa2 j]-

z Л q>< . oZ2

у.(у/ cos 9 + % cos a1) + — sin a1 cos a1 — —— sin a2 cos a2.

Вираз (5.25) дозволяє визначити похибку скручування при розташуванні модулятора Фарадея і поляризатора в одному блоці. Якщо модулятор буде знаходитись в блоці з ана­лізатором, то в четвертому складовому виразі (5.25) необхідно кути ер1 і а1 замінити на

<р2 і а 2.

Розглянемо деякі окремі випадки роботи поляризаційної системи. Допустимо, що по­ляризаційні призми виготовлені так, що кутом між оптичною віссю кристалів і їх робочими гранями можна знехтувати. Тоді друга складова в виразі (5.25) опускається. Якщо нахили і зміщення аналізатора відносно осі OZ відсутні, то вираз (5.25) приймає вид:

тобто похибка пропорційна квадрату нахилу поляризатора і має синусоїдальний характер розподілу по азимуту нахилу з періодом п. При відсутності нахилу і зміщення поляризато­ра залежність похибки від нахилів аналізатора має такий же характер.

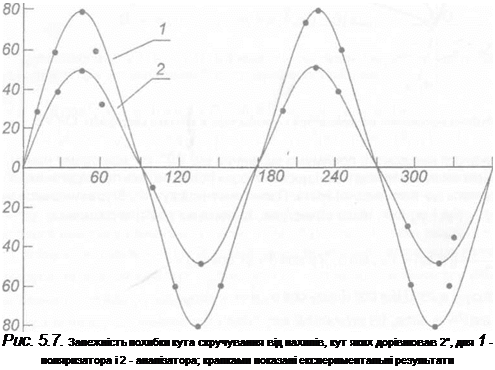
Вирази (5.26) і (5.27) експериментально перевірені [50] на пристрої, аналогічно при­веденому в [38]. Для вимірювання були використані призми, оптична вісь яких паралельна робочим граням. На рис. 5.7 приведені теоретично розраховані криві і результати вимі­рювань, порівняння яких показує їх добре збігання,

д, кут. с

Якщо нахили поляризатора і аналізатора відсутні, тобто призми зміщені паралельно одна другій, то визначення похибки можливо за формулою:

В цьому випадку спостерігається така ж залежність від кута проходження світла, як і при нахилах призм. Проте порівняння постійних величин виразу (5.28) з (5.26) і (5.27) по­казує, що паралельні зміщення призм приблизно в п’ять разів менше впливають на точ­ність, чим нахили будь-якої з призм. У випадку спільного зміщення і нахилів кути q> і у/ впливають на величину похибки в рівній мірі, про що свідчить наявність в виразі (5.25)

2 п

членів, які мають добутки ср^ і (р2цг. Вираз (5.28) має дві складові: , обумовлена

пг

. (п-1)2

похилим проходженням світла через поляризаційні призми, і v ‘ характеризує пово-

п‘

рот вектора напруженості електричного поля при проходженні світла через скло модуля­тора Фарадея. Різні знаки вказують на часткову компенсацію цих двох складових похибки. Компенсацію можна збільшити, якщо в хід променів ввести ще одне плоскопаралельне скло. Тоді формула (5.28) прийме вигляд:

Підставляючи числові значення п0 1,658 і п 1,46 (для плавленого кварцу) отри­маємо, що складова похибки системи з двома пластинами зменшується приблизно в 15 разів і стає зневажливо малою в порівнянні з похибкою поляризаційної системи, яка має одну пластину. Аналогічний результат можна отримати зміною кута падіння світла на пластину модулятора Фарадея шляхом виготовлення її з необхідною сферичністю. Кри­визна поверхні визначається із умови рівності першого і другого членів виразу (5.28). Крім цього, друга складова виразу (5.25) характеризує вплив на точність якості виготовлення поляризаційних призм, тобто непаралельності оптичної осі кристалів призм їх робочим граням, а саме:

8 =——- у1 (у/ sin в + у, sin а^- у2(у/ cos0 + <р2 cosor2)} (5 зо)

пп

Знаючи умови роботи поляризаційної системи, із (5.30) можна визначити вимоги до виготовлення призм. Положення оптичної осі поляризаційної призми відносно її робочої грані можна знайти, нахиляючи поляризатор навкруги осі OY. Тоді вираз (5.30) можна за­писати у вигляді:

а при нахилі аналізатора навкруги осі ОХ — у вигляді:

Із виразів (5.31) і (5.32) видно, що нахиляючи відповідним чином поляризатор або аналізатор і вимірюючи зміну погодженого положення призм, можна визначити кути у1 і

У 2 ‘

Комментарии запрещены.