Бурение грунтовых зондов, установка энергетических колодцев

1.1. ПОНЯТТЯ АВТОМАТИЧНОГО УПРАВЛІННЯ І РЕГУЛЮВАННЯ.

ОБ’ЄКТ УПРАВЛІННЯ

Виконання інженерно-геодезичних робіт припускає використання для вимірювання різних геодезичних приладів або систем. Ці геодезичні прилади чи системи управляються або оператором, або автоматично. В будь-якому випадку вони є об’єктом управління. Та­ким чином, при вирішенні інженерно-геодезичних завдань об’єктом управління може бути геодезичний прилад або більш проста чи складна система автоматичного управління (САУ) приладами, що забезпечує процес вимірювання.

Автоматичні вимірювальні системи взагалі і геодезичні автоматичні прилади і систе­ми зокрема будуються згідно принципів, що викладені в теорії автоматичного управління (ТАУ). Теорія автоматичного управління була розроблена на основі теорії автоматичного регулювання (ТАР). Під автоматичним регулюванням розуміють підтримання постійної або зміну по заданому закону деякої величини, що характеризує цей процес. Це виконується за допомогою вимірювання стану об’єкта або діючих збурень і діяння на регулюючий ор­ган об’єкту.

Задачі автоматичного управління охоплюють автоматичне регулювання і уявляють собою автоматичне здійснення сукупного діяння, вибраного із більшості можливого, на ос­нові визначеної інформації і направленого на підтримку чи покращення функціонування управляючого об’єкту у відповідності з цілями управління. Таким чином, крім задачі регу­лювання, ТАУ вирішує задачі адаптації або самонастроювання у відповідності із зміною параметрів об’єкту чи зовнішнього діяння, задачі формування оптимальних управляючих діянь, автоматичного вибору найкращих режимів із декількох можливих і т. п.

При інженерно-геодезичних вимірюваннях об’єкти управління розміщуються в реаль­них умовах і тому їх стан визначається рядом величин, що характеризують як діяння на їх зовнішнє середовище і управляючі пристрої, так і процеси, що протікають всередині само­го об’єкту. Одні із цих величин вимірюються в процесі роботи (температура, вологість, віб­рація, рефракція і т. п.) і називаються контролюючими. Інші не можуть бути виміряні в про­цесі роботи, хоча і впливають на режим роботи об’єкту. Вони називаються неконтролюю — чими. Таким чином, діянням називається величина, що визначає зовнішній вплив на об’єкт. Якщо діяння виробляється управляючим пристроєм чи задається оператором, то воно називається управляючим діянням.

На об’єкт управління також діє збурення, тобто діяння, що не залежать від системи управління. Збурення діляться на два види: навантаження і перешкода. Перешкоди пов’я­зані з побічними небажаними ефектами (вібрація фундаменту, рефракція атмосфери, гра­дієнт температури) і всяке їх зменшення покращує роботу системи. Навантаження, що змі­нюється в часі, не може бути принципово відділено від об’єкту (наприклад, робота вико­навчих приводів) і об’єкт не може бути принципово захищений від навантаження. Можливо лише зменшення його впливу на якість управління. Контролюючі величини, що характери­зують стан об’єкту, по яких ведеться управління, називаються управляємими або регулю­ючими величинами.

Нарис. 1.1. сукупність контролюючих діянь позначені вектором q = {q1,q2,… ,qj,

неконтролюючих — вектором f — {f1t f2,…, fn}, управляючих діянь — вектором U = {и1;и2,… ,us}, управляємих величин — вектором у = {у1, у2,… ,ук}.

Сукупність контролюючих і неконтролюючих величин однозначно характеризує стан об’єкта і позначена вектором х ={х1,х2,…,х]} . При цьому дотримується умова j>k.

Окремі координати х і у можуть збігатися.

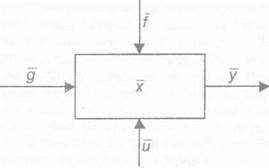В подальшому координати f і q будемо називати координатами зовнішніх діянь, коорди­нати у — управляємими, координати U — управ­ляючими, координати х — стану об’єкта.

Математичний опис об’єкта дозволяє однозначно зв’язати через систему рівнянь управляєм! величини з зовнішніми діяннями, а при визначених початкових умовах ця система рівнянь дозволяє по зовнішніх діяннях f, q, U,

знайти вектор стану х і вихідні управляємі ве-

Рис. 1.1. личини у. Якщо об’єкт характеризується однією

Вектори діяння на об ект управління J

управляючою і однією управляемою величиною,

тобто U і у мають по одній координаті, то

об’єкт управління називається однозв’язаним (простим). При наявності декількох взаємо­зв’язаних координат векторів П і у об’єкт називається багатозв’язаним.

Будь-який об’єкт може розглядатися в умовах статики і динаміки. Якщо и, д, f не

— — 0 і об’єкт знаходиться в статично — off

му стані.

dx

Якщо є залежності u(t), g(t), f(t), то у залежить від t, а — фО і об’єкт знахо-

dt

диться в динамічному стані. Шляхом введення поняття допоміжного вектора, що характе­ризує стан об’єкта, можливо математичний опис динаміки об’єкта записати рівняннями в нормальній формі Коші

x=Vil, q,f, x]

у =prlp, q,f, x}’ ‘

дх. …… .

де х = — и/і і ц/.. — деякі нелінійні векторні оператори, що перетворюють залежні

dt

від часу змінні U, q, f, х. Для вирішення (1.1) необхідно знати початкові умови х(0).

Якщо us дозволяє однозначно задати стан об’єкта, то об’єкт називається управляє — мим. Якщо с/, і ук дозволяють однозначно визначити стан об’єкта, то об’єкт називається повністю спостережним. В загальному випадку об’єкт може бути лінійним або нелінійним. Якщо об’єкт лінійний, то система (1.1) зводиться до системи лінійних диференціальних рівнянь, а якщо об’єкт нелінійний, то система (1.1) записується системою нелінійних дифе­ренціальних рівнянь. Для умови статики об’єкта х = 0, система (1.1) приймає вигляд

Vx-{u, q,f, x}

y = y/y{u, q,f, x}

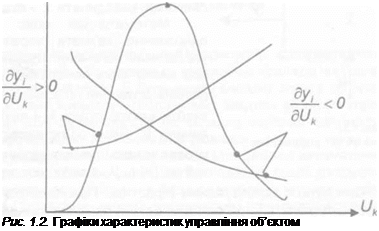де и, g f, у x не залежать від часу. При цьому залежність управляємих коорди­нат у від управляючого діяння називається статичною характеристикою управління. Ха­рактеристика управління (Uk) може бути монотонною, коли dyj/dUk не змінює знак, і екстремальною, коли при оптимальних значеннях Uk = Uk опт тобто dy, / d(Jk = О (рис. 1.2).

Об’єкт може бути стійким, нестійким, нейтральним, стійким в малому, але нестійкий в великому. Стійкий об’єкт повертається в вихідний стан після припинення зовнішнього ді­яння. Аналогом стійкого об’єкту є шарик в улоговині (рис. 1.3а). Нестійкий об’єкт не повер­тається в вихідний стан після припинення зовнішнього діяння, яким би коротким і малим воно не було, тобто управляема координата продовжує змінюватися. Аналогом цього є шарик на вершині горба (рис. 1.36). Нейтральний об’єкт після закінчення діяння встанов­люється в новий стан рівноваги, відмінний від початкового і залежного від виробленного діяння. Аналогом тут є шарик на горизонтальній площині (рис. 1.3в). Рис. 1.3г показує при­клад стійкого об’єкта в малому, але нестійкого в великому.

б)

Рис. 1.3. Приклади положення об’єкту

Комментарии запрещены.