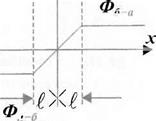Бурение грунтовых зондов, установка энергетических колодцев

В автоматичних інженерно-геодезичних системах часто необхідно виконувати відхи­лення світлового променя на заданий кут в заданому напрямку і розгортання світлового променя в опорну геодезичну площину. Цей процес називається скануванням. В оптико — механічних пристроях процес сканування здійснюється за рахунок руху всієї оптичної сис­теми або за рахунок її окремих елементів таких як дзеркала, призми, клинки, діафрагми (диск Ніпкова). Застосовується також дзеркальне розгортання з багатократним відбиттям і сканування елементами волоконної оптики.

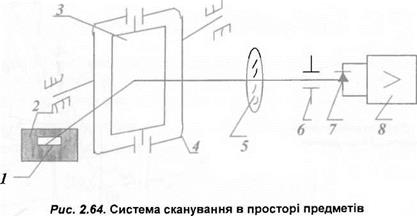
В якості двокоординатного скануючого елемента часто використовують плоске дзер­кало, закріплене в двокоординатному карданному підвісі і установлене на шляху оптично­го випромінювання. Сканування здійснюється поворотом відбиваючої поверхні дзеркала навкруги двох взаємоортогональних осей. Скануюче дзеркало можна установити або до об’єктива, або після об’єктива. В першому випадку це сканування в просторі предметів, а в другому — в просторі зображень. В інженерній геодезії краще здійснювати сканування в просторі предметів (рис. 2.64). На рис. 2.64 позначені: 1 — миттєве поле зору; 2 — поле огля­ду; 3 — дзеркало; 4 — двоступеневий карданний підвіс; 5 — об’єктив; 6 — діафрагма; 7 — фото — діод; 8 — підсилювач.

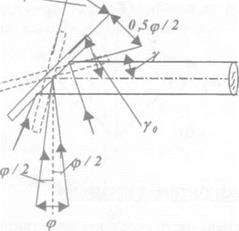
В практиці вирішення інженерно-геодезичних завдань велике значення має зв’язок кутів установлення скануючого дзеркала з кутом поля огляду. Початковий кут установлен­ня скануючого дзеркала відносно оптичної осі об’єктива позначимо у0 (рис. 2.65). Його

значення, як правило, вибирають рівним 45°. Таким чином, приймаючи поле огляду рів­ним ер маємо, що кут коливання дзеркала у визначиться із виразу

0,5(ц/_2

Рис. 2.65. До визначення кута коливання скануючого дзеркала

Траєкторія сканування плоским дзеркалом найбільш просто може бути знайдена при його закріпленні під кутом 45°. Сканування по осі ОХ (рис. 2.66) здійснюється навкруги вертикальної осі карданового підвісу на кут ± /?, а сканування по осі OY здійснюється

поворотом дзеркала навкруги горизонтальної осі карданового підвісу на кут ± Лу — у — у0. Координати зміщення променя мають вид

X = L0tg(3; (2.80)

Y = Ltga = (LJcos p)tga,

де а = 2Ay — кут повороту скануючого поля.

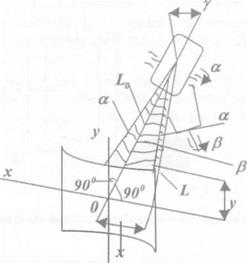Рис. 2.66. До визначення траєкторії сканування

Необхідно відзначити, що тільки середні строчки при а — 0 і у = 0 для любого р, в тому числі р — 0, будуть прямими, а по мірі віддалення від цих ліній буде спостерігатись перекручування поля.

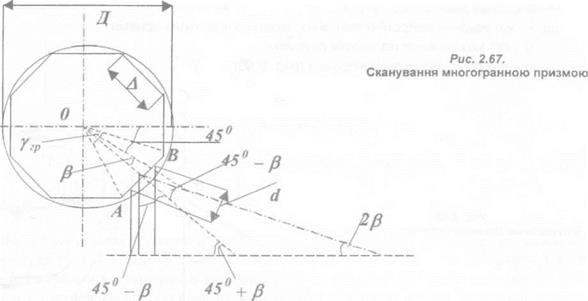Нижче розглянемо сканування многогранною призмою. Перетин обертаючої призми уявляє собою многокутник, габаритні розміри якого цілком характеризуються діаметром Д описаного кола, а положення — кутом 45° + (3 між нормаллю до робочої грані і горизон­тальною віссю (рис. 2.67), де /З — кут сканування.

Кутовий розмір грані визначається центральним кутом

уго = 2л / N = 360°/N,

де N — число граней.

Лінійний розмір грані дорівнює

Л = АВ = 2AOsin(угр / 2) = Д sin(угр / 2). (2.83)

В процесі обертання здійснюється симетричне сканування поля огляду відносно вер­тикалі, причому розмір грані АВ повинен забезпечувати відсутність віньєтировання в ме­жах поля огляду ср0. Кутовий розмір строчки (рс = (р0 зв’язаний з відповідним кутом пово­роту дзеркала ус співвідношенням (рс = 2ус. В той же час ус = т]угр, де tj — коефіцієнт ви­користання дзеркальної грані, і таким чином

срс = 2г/угр = 2г](360° / N) = (720 / N)rj. (2.84)

Перевагою такої системи розгортання є велика частота відтворення площини в полі огляду, що досягається великою кількістю граней призми. Зв’язок між діаметром вхідної зіниці об’єктива d і діаметром описаного кола D записується виразом

sin(45° + р) sin(угр / 2 — (рс / 4)

Викликає інтерес і сканування оптичними клинками. Призма з кутом при вершині д відхиляє промінь світла до основи. При цьому справедливий вираз

sinii.. U _!h_n sin i1 i1 n<

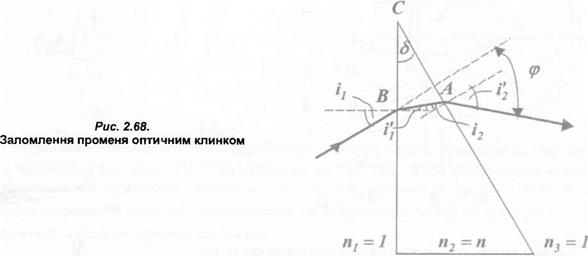де: / — кут падіння випромінювання на передню поверхню призми; і] — кут заломлення на першій поверхні; п — показник заломлення призми (рис. 2.68).

При заломленні на першій поверхні промінь відхиляється на кут і1 -/), а на другій — на кут і2 — /2, тому повний кут відхилення ер буде дорівнювати

<P = U — ‘і +і’2-і2=(п~ 1)(і + і2). (2.87)

Із ЛАВС

5 = ZCBA + ZCAB = п. (2.88)

Так як ZCBA = — -/), a ZCAB = — — /2, то S = і +і2.

Таким чином

<р = S(n-1). (2.89)

Якщо клинок обертати навкруги напряму падаючих на нього променів, то вихідний промінь буде рухатись по твірній прямого кругового конусу з кутом при вершині

2ср = 25(п-1). (2.90)

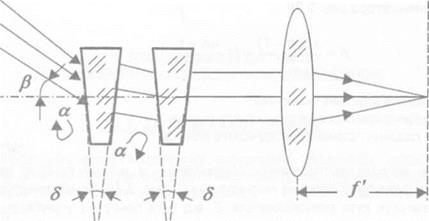
Якщо по ходу променів, падаючих нормально на першу поверхню і які вийшли із клинка, встановити точно такий же другий клинок, то пара клинків буде відхиляти промінь як деякий еквівалентний клинок (рис. 2.69) з кутом при вершині

8еке =2dcos(yl2),

де у — кут між напрямами, що характеризують орієнтацію вершин кожного клинка.

(Pi =SeKg(n-1) = 2S(n-1)xcos(y/2) = (pmax cos(y/2), (2.91)

Де <Ртах = 28(П~ 1).

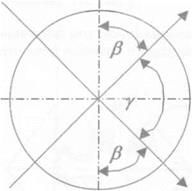
Якщо пару клинків обертати в різних напрямах з однаковою швидкістю, то скануючий промінь буде рухатись уздовж бісектриси кута у (рис. 2.70), тобто уздовж прямої, різним чином орієнтованої на площині в залежності від початкового установлення клинків. Для початкового установлення, що відповідає куту 180°, коли пара клинків еквівалентна плос — копаралельній пластинці, величину сумарного відхилення променя можна виразити через кут (З повороту кожного клинка від початкового положення.

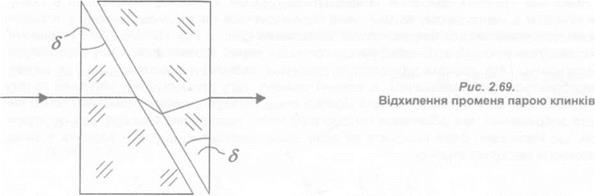Рис. 2.70. Сканування променя
при обертанні клинків

На рис. 2.70 позначені: / і /’ — два положення вершини першого клинка; II і //’ — два положення вершини другого клинка. Так як у = 180° — 2(3, то

<Рї = (Ртах C0S(ї/2) = Ртах C0S(90° ~ Р) = Фтах Sin Р — (2-92)

Якщо пару клинків обертати в одному напряму з однаковою швидкістю, то скануючий промінь буде рухатись по кругу, кутовий розмір якого визначається початковим установ­ленням клинків. Якщо клинки обертати в одному напряму з різними швидкостями, то ска­нуючий промінь буде рухатись по спіралі, шаг якої визначається різницею швидкостей обертання клинків.

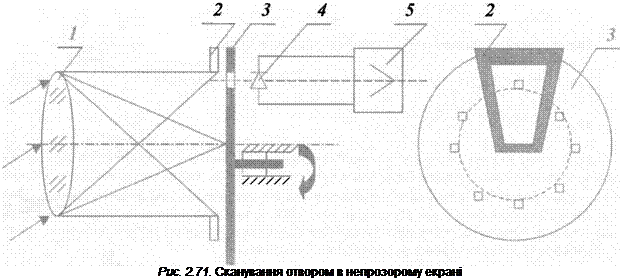Найбільш простим способом реалізації сканування в просторі зображень є скану­вання отвором в непрозорому екрані, який переміщується по заданому закону в площині зображення і створюється ширококутним об’єктивом (рис. 2.71). На рис. 2.71 позначені: 1 — ширококутний об’єктив; 2 — діафрагма поля; 3 — екран з отворами; 4 — фотоприймач; 5 — підсилювач. Така система називається системою сканування миттєвої дії. Тут сигнал, що виробляється фотоприймачем, в кожний момент часу пропорційний величині потоку випромінювання, який проходить в цей момент отвір. Отвори в екрані розміщені таким чи­ном, що зображення, яке обмежене діафрагмою поля, послідовно аналізується по строч­ках так, що коли один отвір виходить за межи вікна діафрагми, другий — входить в вікно, викреслюючи наступну строчку.

Для збільшення частоти сканування застосовується розгортання за допомогою піра­міди. Вісь обертання піраміди розміщують паралельно осі скануючого світлового потоку рис. 2.72а.

а)

Піраміда може бути зрізаною (рис. 2.726), що робиться з ціллю зменшення габаритів і ваги пристрою. Кут відхилення променя Ла дорівнює куту повороту а дзеркальної грані. Теоретично максимальний кут повороту зв’язаний з числом граней піраміди т залежністю

атах(теоР)=2лт — (2.93)

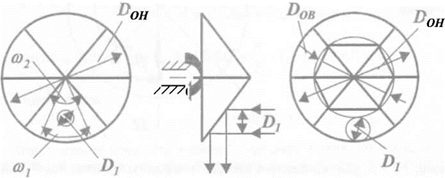
Необхідно відмітити, що відхилення світлового пучка без віньєтирування залежить від апертури D1 відхиляємого пучка, розмірів граней і діаметра D0H нижньої основи піра­міди. При повному перекритті світлового пучка однією гранню кут відхилення дорівнює

(2.94)

де со1 = 2п / т.

Із рис. 2.72

tq(o>2 / 2) = D/(D0H — D), (2.95)

Де D = (D0H + D0B ) / 2, звідки

= 2arctq[D /(D0H — D)J. (2.96)

Тоді максимальний кут відхилення буде

Аа„————— 2arctg(D°H 1). (2.97)

т D

При необхідності створення високої частоти сканування світлового променя викорис­товують пластинчаті дефлектори (рис. 2.73). У цих дефлекторів є відбивач 1, консольно закріплений п’єзоелемент 2, утримувач 3, джерело живлення 4. Дзеркало 1 може бути за­кріплено на боковій поверхні п’єзоелемента або на його торцьовій поверхні.

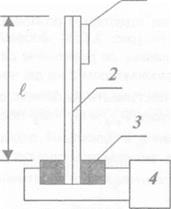Рис. 2.73. Пластинчатий дефлектор

Вираз кута сканування для такого пристрою записується як

aw і аі і

Латдх = Sincot’ (2.98)

і і, ,1

де: d31 — п’єзоелектричний модуль;

І — довжина пластинки;

0 — коефіцієнт динамічності;

ІІт — амплітуда напруги живлення; т — частота сигналів напруги живлення; h — товщина двошарового п’єзоелемента;

Л, — товщина одного шару двошарового п’єзоелемента.

Для отримання інформації про розподіл освітленості в площині зображення в прий­мальну оптичну систему ОЕП вводять спеціальні елементи, що називаються аналізатора­ми.

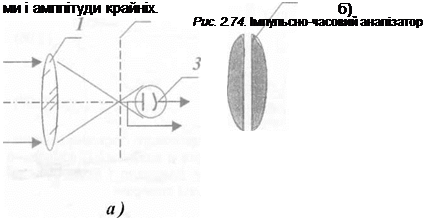
Розглянемо два приклади. Нехай в кутовому полі об’єктива 1 (рис. 2.74а) є три пря­мокутні візирні цілі (рис. 2.746) зображення яких будуються в фокальній площині 2. Пере­міщуючи уздовж осі х перед приймальним фотоелементом 3 непрозорий екран з вузькою прозорою щілиною 4 з постійною швидкістю З, на виході отримаємо світлові імпульси, які відповідають візирним цілям. їх форма і розміщення показані на рис. 2.74в. В залежності від зображення об’єкту і2 форма і амплітуда середнього імпульсу відрізняється від фор­

Ф

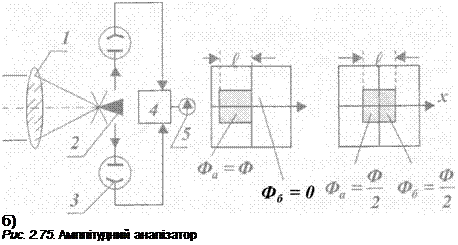
Другим прикладом розповсюдженого амплітудного аналізатора служить світлороз — дільний блок (рис. 2.75а). Зображення прямокутної марки будується об’єктивом 1 в фо­кальній площині, де розміщене ребро світлороздільного кубика 2. Весь світловий потік Ф ділиться аналізатором 2 на дві частини Фа і Фб, які попадають на фотоприймачі 3, сигна­ли з яких поступають на блок порівняння 4, де утворюється їх різниця. Пропорційний цій різниці сигнал Фа_б =Фа — Фб поступає на індикатор 5. При зміщенні марки з оптичної осі її зображення в фокальній площині зміщується (рис. 2.756). Різниця світлових потоків Фа_б буде змінюватись пропорційно цьому зміщенню. Залежність вихідного сигналу від вхідного розузгодження (статична характеристика) має вигляд, який представлено на рис. 2.75в.

Ф

в )

Має місце також аналізатор у вигляді обертаючогося напівдиска, який встановлюєть­ся у площині зображення. При зміщенні зображення буде змінюватись форма і амплітуда сигналу. Такі аналізатори відносять до амплітудно-фазових.

Для компенсації зсуву зображення випромінювача в оптичну систему вводять ком­пенсатор, який розміщують або перед об’єктивом, або між об’єктивом і аналізатором. В першому випадку компенсатор працює в паралельному пучку променів, а в другому ви­падку — в збіжному пучку променів. Найбільшого застосування має компенсатор, який пра­цює в паралельному пучку променів. Прикладом такого компенсатора є два обертальних в протилежні сторони з однаковою кутовою швидкістю оптичні клинки (рис. 2.76).

l і/ і і Рис. 2.76. Компенсатор з двома оптичними клинками в паралельному пучку променів

Залежність кута розузгодження на вході оптичної системи (3 від кута повороту ком­пенсатора а має вид

Р = 2S(n -1)sina, (2.99)

де: S — заломлюючий кут оптичних клинків;
п — показник заломлення матеріалу.

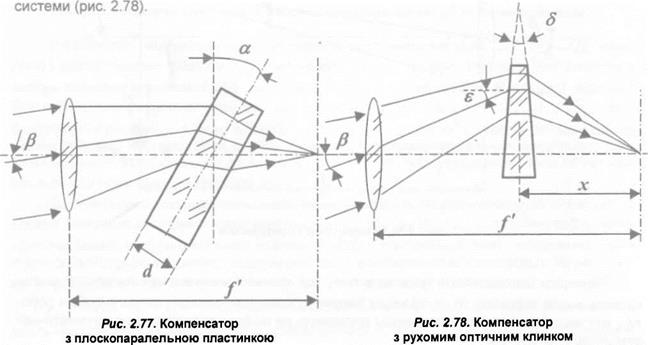
Прикладами компенсаторів, які працюють в збіжних пучках променів є плоскопара — лельна пластинка (рис. 2.77) і оптичний клинок, що переміщується уздовж оптичної осі

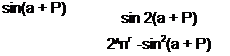Залежності кута розузгодження р від кута нахилу а і лінійного зміщення х для цих компенсаторів визначаються виразами: а) для компенсатора рис. 2.77

б) для компенсатора рис. 2.78

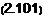х8(п-1) м ~ — + (U 2п‘

де: Р — фокусна відстань об’єктива;

d — товщина плоскопаралельної пластинки; є — кут падіння променя на поверхню клинка.

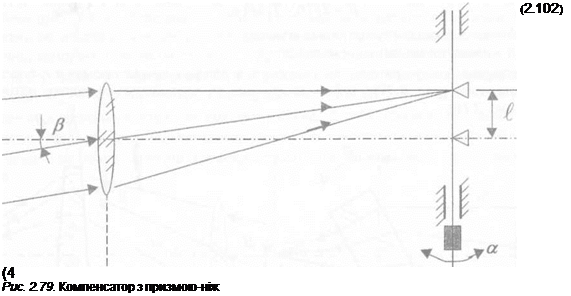Має також широке застосування компенсатор, в основі якого є призма-ніж, що переміщується в фокальній площині на величину і (рис. 2.79) по мікрометреному гвинту з шагом S. Залежність кута розузгодження р від кута повороту гвинта а визначається формулою

Ґ

Перевага компенсаторів полягає в тому, що звично малим значенням кута р відпо­відають великі значення а, х та інших параметрів, що змінюються, так що похибки робо­ти з компенсаторами незначним чином впливають на вихідне розузгодження автоматичної вимірювальної системи.

Розділ III

Комментарии запрещены.