Бурение грунтовых зондов, установка энергетических колодцев

Основное уравнение гидростатики:

Р=Р0 + рёИ, (5.19)

где Р — абсолютное статическое давление, Па; Р0 — внешнее стати­ческое давление, Па; И — глубина, измеряемая по вертикали, м.

Следствием основного уравнения гидростатики является закон Паска­ля: внешнее давление передается во все точки жидкости без изменения.

Уравнению (5.19) можно придать иной вид:

(5.21)

В дифференциальной форме записи, справедливой как для жид­костей, так и для газов,

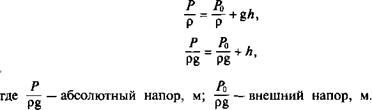
(5.22)

где р = р(Р)— уравнение вида термодинамического процесса измене­ния состояния жидкости (газа).

Экспериментально доказано, что основные параметры состояния реального газа (Р, Т, р, У^, V) приближенно связаны между собой в любом термодинамическом процессе в данный момент времени урав­нением состояния совершенного (идеального) газа (уравнением Клапей­рона — Менделеева) (5.23) — (5.26).

Совершенным называют газ (смесь газов), подчиняющийся уравне­нию состояния.

Чем меньше плотность реального газа, тем меньше его поведение отличается от поведения совершенного газа. При этом справедливы следующие зависимости:

рул=лт-, РУ= тЛТ; Р^УЛ = ^ЫЯТ; Р=рЯТ,	(5.23) (5.24) (5.25) (5.26)

где Л —удельная газовая постоянная, Дж/(кг • К); т — масса газа, кг; цм — молярная масса газа, кг/кмоль; для воздуха цм = 28,97 кг/кмоль;

= Ь — — молярный объем газа, м3/кмоль; при нормальных (физи-

ческих) условиях (Р= 101 325 Па, Т= 273,15 К) для любого совершен­ного газа цм = 22,41410 м3/кмоль; цмЛ — универсальная газовая по­стоянная, ц. мЯ = 8314,51 ДжДкмоль • К):

(5.27)

8314,51

Им Им

1 Iсмоль (киломоль) — условная единица количества вещества, содер­жит количество частиц, равное числу Авогадро (6,022 • 1026 кмоль1).

Количество вещества равно 1 кмоль, если число килограммов веще­ства равно относительной молекулярной массе:

цм = Mr ■ 1 кг/кмоль, (5.28)

где Mr — относительная молекулярная масса.

Мг = ‘^(пЗТ1АГ1), (5.29)

/ = |

где яат — число атомов в молекуле химического элемента; Аг — отно­сительная атомная масса химического элемента; у — количество хими­ческих элементов в соединении.

Единицей количества вещества в СИ является 1 моль, однако удобнее пользоваться в расчетах величинами, в которые входит кмоль.

Связь между начальными и конечными значениями параметров состояния в изохорном (р = const, или г) = const), изобарном (Р= const) и изотермном (Г= const) термодинамических процессах определяет объединенный газовый закон:

= Д = const. (5.30)

-*/ Рм/

Процесс изменения состояния газа по глубине примем изотерм- ным. Решая совместно (5.22) и (5.30) после интегрирования, получим основное уравнение газовой статики:

Р = Р, е^, (5.31)

где е ~ 2,72 — основание натуральных логарифмов.

Или

P = Po^F, (5-32)

В уравнениях (5.19), (5.31) и (5.32) при рассмотрении статики жидкости (газа) в буровой скважине следует учитывать возможный наклон скважины:

h = L cos 0, (5.33)

где L — длина ствола скважины, м; 0 — среднее по длине скважины значение зенитного угла.

Разница между абсолютным и внешним давлениями жидкости на­зывают весовым давлением Рв,

P-P0 = PB = pgh, (5.34)

Р Р — Р

— = ——— (5 35)

pg pg ’

Рв

где — — весовой напор жидкости, м.

При Р0 = Ра (сосуд открыт, жидкость граничит с атмосферой) Р„ = Ря. Разницу между абсолютным и атмосферным давлениями назы­вают избыточным (манометрическим, сверхатмосферным) давлением Р„ и измеряют манометром.

Р-Р^Р«, (5.36)

Р Р — Р

— = ——— (5 37)

pg РВ ’ 1 ‘

р

где — избыточный (манометрический, сверхатмосферный) напор, м.

Разницу между атмосферным и абсолютным давлениями называ­ют вакуумметрическим давлением Ртк и измеряют вакуумметром.

Рл-Р=Рт (5-38)

Р Р — Р

юк а (5.39)

pg Pg

р

* на

где —— вакуумметрическии напор, м.

г О

Определим максимальное значение высоты всасывания (вакуум- метрического напора) воды насосом в атмосферных условиях; при вса­сывании в камере насоса Р>РНП. Примем Р=РНП. При / = 4°С Ра = 0,981 • 105 Па, р = 1000 кг/м3, РИП ~ 0. Тогда (5.39) примет вид:

Рык „ Р,-Р Рш — о 0,981 -105 1П

Комментарии запрещены.