Бурение грунтовых зондов, установка энергетических колодцев

По буримости методом плавления все горные породы можно разделить на низкотемпературные (лед, сера, каменная соль) и высокотемпературные (гранит, глина), плотные и пористые, связ­ные и рыхлые [63]. Отдельно могут быть выделены породы мало­эффективные для бурения плавлением, при нагреве которых про­исходит выделение газообразных и тугоплавких элементов (изве­стняк, доломит).

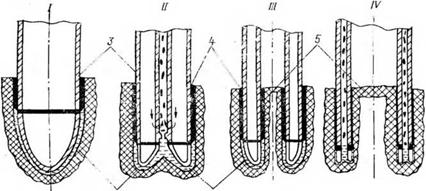
В зависимости от способа удаления расплава из зоны забоя все разнообразные конструкции буровых устройств для плавления скважин могут быть разделены на два основных типа: уплотняю­щие— для плавления в пористых породах; экструзионные (выдав­ливающие) — для плавления в плотных породах (рис. 5.1). Уплот­няющие буровые устройства, расплавляя пористые породы или грунты, обеспечивают затвердевание всего расплава в уплотнен­ном и остеклованном слое на стенках скважины (керна). Для кон­тактного бурения плавлением с отбором керна должны применять­ся специальные колонковые буровые снаряды как уплотняющего, так и выдавливающего типа, конструкции которых характери­зуются наличием кольцевого нагревателя, керноприемной трубы и системы охлаждения, обеспечивающей затвердевание расплава как на стенках скважины, так и на поверхности керна.

Многие технологические процессы сопровождаются плавле­нием твердых тел при контакте с поверхностью, разогретой до тем­пературы, превышающей температуру плавления. Образующийся при этом расплав течет под действием внешней силы со стороны греющей поверхности или плавящегося образца. Такие явления сопровождают плавление в контактных плавильных аппаратах,

2 1 Рис. 5.1. Схемы конструкций основных типов пенетраторов. I — сплошные уплотняющие; II—сплошные экструзионные; III — кольцевые уплотняющие; IV — кольцевые экструзионные. 1 — расплав горной породы; 2 — горная порода; 5 —пеиетратор; 4—остеклованный слой; 5—керн

сварку плавлением, пайку и др. Несмотря на распространенность, этот сложный многопараметровый процесс остается теоретически и экспериментально слабоизученным. Опубликованные исследования зачастую основаны на простейших балансовых соотношениях, что не позволяет учесть влияние многих важных в практических при­ложениях факторов. Экспериментальное изучение закономерностей процесса контактного плавления, его математическое моделирова­ние становятся особенно актуальными при решении различных технических проблем, возникающих в ходе новых разработок, а также при совершенствовании созданных ранее конструкций и тех­нологий. Это непосредственно относится и к новому способу буре­ния горных пород плавлением [63, 64].

Исследование и разработка технических средств и технологии бурения плавлением является одним из перспективных направле­ний повышения эффективности проходки скважин в сложных гео­логических и горно-технических условиях на основе нетрадицион­ных способов разрушения и крепления горных пород. В основе технологии бурения скважин способом плавления лежат чисто фи­зические процессы разрушения горных пород, связанные с измене­нием агрегатного состояния последних в результате интенсивного теплового воздействия в зоне забоя скважины. Процесс бурения плавлением определяется в основном температурой и теплофизиче­скими свойствами проходимых пород и мало зависит от их меха­нических свойств. Последнее обстоятельство обусловливает уни­версальность рассматриваемого метода бурения для большинства горных пород, представляющих собой обычно полиминеральные многокомпонентные системы, преимущественно силикатного со­става (75 % земной коры по данным А. Е. Ферсмана), температур­ный интервал плавления которых находится в пределах 1200— 1700 К при атмосферном давлении. В отличие от механического бурения рассматриваемый способ с увеличением глубины сква­жины и соответствующим ростом естественной температуры по­роды повышает свою эффективность. Этот новый способ бурения скважин позволяет решать задачу поддержания устойчивости • и закрепления стенок скважины и керна непосредственно в процессе бурения путем создания за счет застывающего расплава прочного водонепроницаемого стекловидного слоя. Так как при бурении плавлением отпадает необходимость во вращательном или ко­лебательном движениях бурового инструмента, существенно сни­жаются потери энергии при передаче ее к забою, появляется воз­можность точнее выдерживать заданное направление сква­жины.

Отличительными особенностями технологии бурения плавле­нием являются высокая концентрация в зоне забоя скважины теп­ловой энергии, эффективная передача ее породам с целью обеспе­чения заданной скорости плавления, выдавливание расплава из зоны забоя, формирование на стенках скважины монолитного и прочного остеклованного слоя, удаление продуктов расплава из скважины на поверхность или в специальный шламосборник цир­кулирующей промывочной средой.

Передача тепловой энергии к поверхности забоя в общем слу­чае может осуществляться излучением, конвекцией и контактной теплопередачей. Однако необходимость использования в процессе бурения скважины жидкостной или газообразной среды с пара­метрами, определяемыми в основном требованиями очистки сква­жины от продуктов разрушения и поддержания в устойчивом состоянии ее стенок, затрудняют и ограничивают возможности ис­пользования двух первых видов теплообмена. Более широкое при­менение в настоящее время получает метод контактной передачи тепла от поверхности нагревателя к плавящейся поверхности за­боя через образующийся между ними слой жидкого расплава.

Благодаря специфическим особенностям техники и технологии бурение скважин плавлением дает принципиальную возможность реализовать следующие потенциальные преимущества [15, 26, 28, 63].

1. Беструбное бурение скважин с помощью полуавтономных буровых снарядов на грузонесущем кабеле или шлангокабеле по­зволяет исключить трудоемкие и длительные спуско-подъемные операции, устранить потребность в громоздких и тяжелых буро­вых вышках и мачтах, повысить до 90 % КПД передачи энергии с поверхности к забою, скважины, улучшить такие важные эконо­мические показатели бурения, как трудозатраты, металлоемкость, энергоемкость и др., а также успешно решать задачи оптими­зации и комплексной автоматизации как основных, так и вспомо­гательных процессов и операций, связанных с бурением сква­жины.

2. Одновременное с бурением закрепление стенок скважины в слабосвязных и неустойчивых горных породах за счет создания прочного и непроницаемого остеклованного слоя позволяет упро­стить конструкцию скважины, резко снизить расход обсадных труб н тампонажных материалов, затраты времени и средств на тру­доемкие и дорогостоящие работы по креплению скважины обсад­ными колоннами.

3. Сохранение в процессе бурения (за остеклованным слоем) естественных фильтрационных свойств коллекторов позволяет по­высить качество опробования скважин и эффективность эксплуа­тации продуктивных горизонтов в сложных горно-геологических условиях.

4. Отсутствие в скважинах колонн обсадных труб позволяет повысить результативность методов каротажа и скважинной гео­физики.

На современном этапе имеется достаточно оснований считать актуальным проведение аналитических и экспериментальных ис­следований процесса бурения скважин плавлением, направленных на разработку технических средств и технологий в целях быстрей­шей практической реализации преимуществ этого нового перспек­тивного способа бурения скважин.

5.1. ТЕОРЕТИЧЕСКИЙ АНАЛИЗ ПРОЦЕССОВ ТЕПЛОМАССОПЕРЕНОСА ПРИ ПЛАВЛЕНИИ ГОРНОЙ ПОРОДЫ НА ЗАБОЕ СКВАЖИНЫ

Большинство теоретических исследований явлений тепломас­сообмена, лежащих в основе технологических процессов, связан­ных с контактным плавлением твердых тел, выполнено при по­стоянных значениях физических и теплофизических параметров этих тел и их расплавов, осредненных для широкого интервала температур [3, 18, 48, 60, 64, 69]. Однако при высоких температу­рах, близких к температурам агрегатного перехода (плавления), свойства горных пород и их расплавов могут существенно зави­сеть от температуры. Особенно это относится к реологическим свойствам расплавов горных пород, где эта зависимость для тем­пературного диапазона плавления пород существенно нелинейна. Все это предопределяет возможные значительные погрешности при исследованиях задач тепломассопереноса в линейной постановке.

С целью анализа эффективности процесса бурения горных по­род плавлением исследуем* рассмотренную в разделе 4.2 матема­тическую модель контактного плавления породы на забое сква­жины, предполагая, что теплофизические параметры среды являются функциями температуры, а слой расплава породы пред­ставляет собой несжимаемую жидкость со сложной реологией.

, Рассмотрим наиболее важный с практической точки зрения установившийся режим бурения с постоянной скоростью углубки скважины v = const. Для контактного плавления породы забоя используются нагревательные устройства с двумя принципиально разными формами контактирующих с забоем поверхностей: 1) по­верхность с осевой симметрией, полученной при вращении обра­зующей вокруг оси скважины, — для бурения скважин сплошным забоем; 2) криволинейная поверхность кольцевого нагреватель­ного устройства, один из размеров которой достаточно велик по сравнению с двумя другими характерными размерами, — для бу­рения скважин кольцевым забоем с отбором керна. —

Полная математическая модель процесса бурения скважин плавлением предполагает совместное решение уравнений, описы­вающих процессы тепломассопереноса в криволинейном слое рас­плава и распределения температуры в нагревательном устройстве и в окружающем массиве.

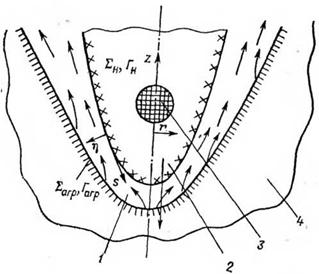
Так как схемы вывода уравнений для двух типов нагреватель­ных устройств принципиально не отличаются друг от друга, ‘.рас­смотри*! лишь первый тип греющей поверхности — осесимметрич­ный. По аналогии с исследованием задачи тепломассопереноса для постоянных_значений теплофизических и реологических харак­теристик сред, рассмотренной в разделе 4.2, ‘введем, как показано на рис. 5.2, связанные с нагревательным устройством системы ци­линдрических г и 2 и криволинейных s, т] координат. Как и в раз­деле 4.2, обозначим через 60 и w0 неизвестные пока масштабы толщины слоя расплава б и продольной скорости его течения ws

Рис. 5.2. Схема процесса контактного плавления горных пород при буре­нии скважины. 1 — слой расплава; 2~ корпус нагревательного устройства; 3 — тепловыделяющий эле­ мент; 4 —массив горных по­род.

и введем следующие безразмерные характеристики и независимые переменные:

TOC o "1-5" h z п____ Г. 7__ . о________ .

К 1 , 1 , С> ^ ,

’І б — Аб / ’ б0 ’

р = Л. ^

7 /Г» » > ^Ї1

о ’ я и>0 ’ 1 ю0рт

Л (>к ^агр _ 11 (V. *ж)

*чч)

®ж = 7——- — Г-’ М =

ЮоЦ-ІЇО. ^алр — ^«,)1

К

° — »* ^0 ьж лж

гЬ„ да/

ш.— ■ рР —

0 „ , ч ’ „о

“Ж (^агр ^оо)

2^. . ^ РежД

^жРж ^агр *«)

Здесь / — характерный размер нагревательного устройства; р — давление в слое расплава; С —внешняя нагрузка на нагрева­тельное устройство; Шп — ортогональная составляющая скорости течения расплава; ц — динамический коэффициент вязкости рас­плава; уо’—характерный масштаб у, у=-у/2//, // — второй инва­риант тензора скоростей деформации; т5,ь тп», — касательные составляющие вязких напряжений в слое расплава; с^, Ъ°ж, —

характерные значения коэффициентов теплоемкости, теплопровод­ности и температуропроводности сред; индексы «ж», «т», «агр», «оо» — относятся соответственно к жидкой и твердой фазам, гра­нице фазового перехода и к горному массиву в бесконечно уда­ленных точках.

Переходя в общих уравнениях неразрывности и движения к безразмерным координатам и применяя к ним методы теории по­добия и анализа размерностей, находим выражения для опреде­ления масштабов продольной скорости течения расплава в зазоре о>о и толщины слоя расплава 6о

^РтЦ (®о/^о» ^агр) ш/рж

(5.1)

(5.2)

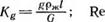из которых получаем следующие соотношения, определяющие три основных безразмерных комплекса Ке, Ке, /С6, характеризующие перенос массы и импульса в слое расплава:

к’/ртА’/б

РжЮ

Как показали исследования, выполненные в работе [65], комп­лексы Кв, Ие и К6 для условий бурения плавлением горных пород во многих случаях довольно малы, поэтому в уравнениях пере­носа в слое расплава можно пренебречь всеми величинами по­рядка 0(Ке, Йе, Кь), что позволяет считать в рамках выбранной точности давление в слое расплава функцией только одной коор­динаты 5, т. е. Я == Р(х).

Число Бринкмана Вг, определяющее роль диссипативного ра­зогрева в слое расплава, при контактном плавлении твердых тел с большими энергетическими мощностями также мало (при плав­лении горных пород Вг » 10~4-Ь 10~3), что позволяет существенно упростить и уравнение переноса тепла в слое расплава.

Таким образом, ^истема уравнений, описывающая тепломассо — перенос в слое расплава, может быть представлена в виде

д

ди

где у=1 соответствует осесимметричной, а у = 0 — плоской кар­тине течения расплава соответственно для условий работы сплош­ного и кольцевого нагревательных устройств.

Вид граничных условий для системы уравнений (5.3) — (5.5) в общем случае зависит от особенностей конкретной реализации процесса контактного плавления. Однако при этом условия на по­верхности плавления забоя скважины (V — 1) и на рабочей (грею­щей) поверхности нагревательного устройства (V = 0) остаются без изменения и с точностью до величин 0(/(6) могут быть запи­саны в следующем виде:

а) при 1] = 0 (Л = иц — 0;

TOC o "1-5" h z „о = <2» (5.6)

■ч-0 Л’вд С

б) при 11=1; Us— 0; иц = —dRH/dS„;

e»l,., = 0; = + (5.7)

Здесь 0„ — приведенная температура рабочей (греющей) по­верхности нагревательного устройства; QH — приведенная плот­ность теплового потока, подводимого к рабочей поверхности со стороны нагревательного устройства; QT — безразмерная плотность теплового потока, поступающего со стороны забоя в горную по­роду.

Система дифференциальных уравнений (5.3) — (5.5) с гранич­ными условиями (5.6)-(5.7) может служить основой для построе­ния замкнутых математических моделей процессов тепломассопе — реноса с нелинейными теплофизическими (сжДж) и реологическими (jl) свойствами расплава горных пород.

Тепловое взаимодействие слоя расплава с породой забоя оп­ределяется плотностью теплового потока на поверхности плавле­ния со стороны забоя в горную породу QT, а последнее зависит от распределения температуры в горной породе 0Т. Таким обра­зом. задача о температурном поле в горной породе представляет собой одну из основных составляющих общей математической мо­дели контактного плавления.

Если форма поверхности плавления забоя задана, то задачу о температурном поле в твердой фазе можно рассматривать как самостоятельную и исследовать независимо от других задач общей модели.

Введем, как показано на рис. 5.2, для области Q в твердом плавящемся материале декартову систему координат х, у, z и свя­жем ее с поверхностью нагревательного устройства Еи таким об­разом, чтобы ось z была направлена в сторону, противоположную вектору V. Тогда краевая задача о распределении температуры в твердом плавящемся материале tT в области й может быть сфор­мулирована в безразмерной постановке

—Рест (®т)-^т + div [Ят (0Т) grad 0Т] = 0 (5.8)

с граничными условиями

Г 1. (*, ¥> 2)е2агр; НтІ2агр=2. 1 0,, (X, К, г) є 2,;

(5.10)

Пт ©т(А, к, г) = о, (х,-к, і)єй.

ХІ ,о ’

ХЧУ’ + 2;->0

В уравнениях (5.8) — (5.10) использованы следующие обозна­чения:

Перейдем в выражениях (5.6) — (5.8) к параболическим коор­динатам (о, т), которые определяются соотношениями

2г == (т2 — а2), г — от.

Пусть поверхность плавления ЕаГр или с точностью 0(Лд) грею­щая поверхность 2н совпадает с координатной поверхностью о — = ао. Тогда краевая задача (5.8) — (5.10) становится одномерной и может быть представлена в виде

0

(5.11)

с граничными условиями вт|а=(Уо=1, Нтвт —0.

Для решения задачи (5.11) разработан численный алгоритм [65]. Для случая, когда теплофизические параметры твердого тела постоянны, задача (4.14) решена аналитически в замкнутой форме [65]. Найденное решение позволило представить ^безразмерную плотность теплового потока в горную породу фт в виде

оо

оо а

оо

Полученные выше дифференциальные уравнения и граничные условия могут служить основой для построения замкнутых мате­
матических моделей процессов тепломассопереноса с нелинейными свойствами теплофизических и реологических сред при сравни­тельно малой толщине слоя расплава в зазоре между нагрева­тельным устройством и поверхностью плавления забоя, т. е. при Кд< 1.

Введем вспомогательную функцию g(x. t) такую, что функция хц(х. t) является обратной к g(x, t). При этом равенство (5.2) можно представить в виде

Рж 6

Тогда, очевидно, что из уравнения (5.4) следует

— т1о)’ 0ж] sign (ч — Чо), (5.13)

где

g(x, вж) = £(Ял, Gx, tJ/glKл, G(tarp — tJ];

r]o— точка, где dUs/di] — 0.

Из уравнений (5.3) и (5.13) с граничными условиями (5.6) и (5.7) получим

»1

Us = b g (—,л||-1ч —Чо1. ©ж) sign (г) — т]0) rfrj; (5.14)

о

u’ = l?~k fA2/?V (-Д S-l ^ “ Чо I, еж)(1 — ч) sign (ч — Чо) dr] j,

(5.15)

где константа rjo определяется из соотношения i

Л7£Г|11 —^ 0ж) sign (ч — Чо) ^Ч = 0. (5.16)

о

Из выражения (5.15) и граничного условия для при i] = 1 после интегрирования по 5 получаем

Rv+’-R:+1 г _/ Л dP

(v+ 1 )A2RV

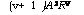S В (~Л тЬ"1 Ч — Чо I. ©ж) sign (ч — Чо) Ч Л,- (5.17)

Это в общем случае нелинейное дифференциальное уравнение первого порядка для функции /э(5).

Будем считать, что в районе концов образующей рабочей по­верхности (5 = 5], 5 = 52) поддерживаются заданные значения давления /Э(5])=Р1 и Р(5>2) = Р2■ Первое из этих условий опре­деляет константу интегрирования уравнения (5.13), а второе позволяет найти постоянную /?*, которую при А?* е [/?„(5|),/?„(52)] можно интегрировать как координату точки разветвления потока расплава, где

= 0 (ив = 0).

Далее, подставляя выражения (5.14) и (5.15) в уравнение (5.5), получаем интегрально-дифференциальное уравнение для на­хождения ©ж. Граничные условия по координате т] заданы и опре­деляются соотношениями (5.6), (5.7). В точке R = R* уравнение (5.17) вырождается. При этом естественно потребовать ограничен­ности производной двж/dS, что дает граничное условие по коорди­нате s, необходимое для решения уравнения переноса тепла в слое расплава.

Кроме того, очевидно, что осевая нагрузка, приложенная со стороны греющей поверхности нагревательного устройства к слою расплава, уравновешивается силами внутренних напряжений в жидкой фазе, которые с. точностью до слагаемых порядка 0(К&) представлены силами давления. Таким образом, нетрудно записать дополнительное условие

*—— [RP — dS=l. (5.18)

*i(S2)-Si(Si) г dS

Для случая, когда рабочая поверхность нагревательного уст­ройства изотермическая (0Н = const) и имеет форму параболы, а расплав является жидкостью, реологические свойства которой описываются степенным реологическим уравнением, построенная система интегрально-дифференциальных уравнений после преоб­разований приводится к системе конечных уравнений, удобных для инженерных расчетов.

Пусть

ц = [ & (0>К)/ДЕ (5.19)

тогда из выражений (5.14), (5.15) имеем

и*=\ ГШ Гsign (% — ц) rfT)Ale+ 1>/е (~ S’)17′: <5-20>

о

где

° = ~ I тш Г 11 Sign (т|° ~ Т|) dr];

О

•п

Ф(Т1) = Г] ^ | ^°(~J |1/е sign fa — Г]) dr] —

я

f^prisignfa-rOrfri.

о

Точка г)о определяется из соотношения i

|т(0^ |1/е sign (-*1° — — г,) dn = °. (5.22)

Краевая задача для температуры 0Ж в соответствии с уравне­нием (5.5) и граничными условиями (5.7) на поверхности т] = 1 примет вид СЖФ (т1) Л д РежЛ ёвж ё

{к-к)

(5.23) (5.24)

D

dr di

при

I _______ (Л.__________ Яж dS lrj=I и> ^ д

В.

где

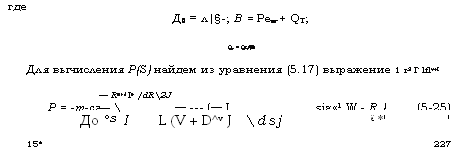
Д0 = л|§-; В = Pew + QT; QT = Qt/’-[s ■ Для вычисления P(S) найдем из уравнения (5.17) выражение 1 г2 Г lflv+I — Rv+l Iе /dR2Ј Р = — т-сг— ——- (— I sig«1 W — R.) (5-25) До °S I L (V + D^v J dsj ё *’ ‘ 15* 227

0,4 " e*PilB/(W>]. «=0,8. агр + Р(<-<агр)"

Л-Яг_ +

0,2 0,4 0,6 О, В 1}

Рис. 5.3. Распределение давления Р 1,6 и толщины слоя расплава б вдоль рабочей поверхности нагревателя (а), скоростные профили и& и в слое 4? расплава (б) и распределение темпе­ратуры 0 и суммарного теплового потока N по толщине слоя распла­ва (в).

0,8

Константа До определяется из выражения (5.18)

Яг _ I -,г+1 пГ+1 ■ Е, ло ч 2е

(5.26)

Система уравнений (5.13) — (5.22) замкнута и позволяет найти такие характеристики процесса контактного плавления, как 0Н, <Э„, Ре, (}т, <ЭЖ, А, и в, ип, Р.

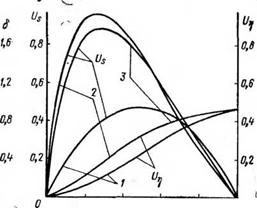
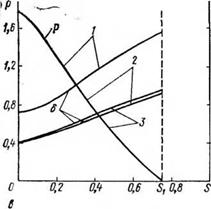
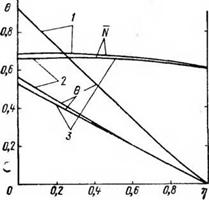
С этой целью разработан и реализован на ЭВМ алгоритм чис­ленного расчета процесса контактного плавления горных пород при бурении скважин. Результаты выполненных вычислений, ил­люстрирующих зависимость параметров процесса тепломассопере — носа от нелинейности теплофизических и реологических характе­ристик горных пород и их расплавов, представлены на рис. 5.3.

Анализ выполненных расчетов позволяет в каждом конкретном случае для различных типов горных пород выбрать режимы плав­ления, обеспечивающие минимальные потери тепловой энергии, т. е. позволяющие вести процесс с максимальным КПД [39,61,66].

Комментарии запрещены.