Бурение грунтовых зондов, установка энергетических колодцев

Бурение горных пород плавлением с помощью высокотемпе­ратурного жаропрочного пенетратора является результатом со­вместного проявления сложных тепломассообменных и гидродина­мических процессов, точное описание которых представляет серьез­ные математические трудности [17, 18, 40, 48, 61, 65, 67 и др.]. Вместе с тем интересы практического освоения перспективного спо­соба бурения горных пород плавлением настоятельно требуют разработки инженерной методики конструктивных и технологиче­ских расчетов, связанных с проектированием макетов и опытных образцов высокотемпературных пенетраторов, режимных парамет­ров бурения плавлением в породах с различными физическими и теплофизическими свойствами, а также расчетов, ‘ позволяющих оценивать значения таких важнейших характеристик процесса бу­рения плавлением, как температура рабочей поверхности пенетра­тора, толщина слоя расплава породы под пенетратором, темпера­тура расплава и связанная с ней вязкость и пр. Единственный выход в данных условиях — разработка приближенной методики расчетов, не противоречащей физике явлений, сопровождающих процесс бурения плавлением, увязывающей воедино влияние всех основных определяющих процесс факторов и обеспечивающей до­статочную для практики точность.

При разработке приближенной методики расчета процесса бу­рения горных пород плавлением без отбора керна тепловым пене­тратором уплотняющего действия примем следующие исходные положения и упрощающие допущения.

1. В качестве внешней формы рабочего органа — пенетрато­ра— принимается тело вращения цепной линии вокруг ее верти — калькой оси. Эта форма выгодно отличается от других вероятных форм (цилиндр, конус, полусфера, параболоид вращения) возмож­ностью в широких пределах варьировать высотой пенетратора, со­храняя в любом случае плавный переход в цилиндрическую форму в верхней части, которая необходима для надежного формирова­ния оплавленных стенок скважины. В сравнении с другими избран­ную форму можно считать наилучшей с тепловой и гидродинами­ческой точек зрения.

2. Рабочий орган — пенетратор с расположенным внутри ис­точником тепловой энергии в виде высокожаропрочного электро­сопротивления — рассматривается как тело с равномерно распре­деленным источником.

3. Процесс бурения горных пород плавлением рассматривается при установившемся режиме. Как показано С. С. Силиным [1965 г.] на примере плавления льда, установившийся режим на­ступает через несколько секунд после начала процесса. По этой причине при анализе процесса бурения горных пород плавлением нет нужды учитывать фактор времени, что существенно упрощает постановку и решение задачи.

4. Теплофизические свойства полиминеральной горной породы характеризуются некоторыми средними значениями плотности, теп­лопроводности и теплоемкости.

5. Температура рабочей поверхности пенетратора и толщина слоя расплава породы под пенетратором характеризуются их не­которыми средними значениями.

6. Вязкость породного расплава принимается при температуре, средней между температурой плавления породы (агрегатного пе­рехода) и температурой поверхности пенетратора.

7. Верхний торец пенетратора теплоизолирован и в теплооб­мене не участвует.

8. Рассматривается двухмерная тепловая задача в постановке, упрощенной с помощью принципа элементарной суперпозиции [37], в соответствии с которым реальный пенетратор представлен в виде эквивалентного по объему V цилиндра радиусом /?, равным радиусу верхнего торца пенетратора, и высотой Нч— У/(пЯ2).

9. Радиальное рассеивание теплоты в массиве в связи с крат­ковременностью теплового воздействия пенетратора на форми­руемые им стенки скважины определяется как одномерный тепло­вой поток в полуограниченное тело.

Введем понятие активной тепловой мощности пенетратора Ыя, под которой будем понимать ту часть его общей электрической мощности, которая затрачивается на собственно бурение горных пород плавлением, поскольку возможны не учитываемые данной теорией потери теплоты, например, связанные с принудительным охлаждением подводящих коммуникаций или с промывкой сква­жины в целях транспортирования продуктов расплавления вполне монолитной породы с верхнего торца пенетратора к устью.

Активная тепловая мощность пенетратора Na при установив­шемся процессе бурения плавлением расходуется на перегрев

окружающего расплава фь на скрытую теплоту плавления породы С* на нагрев массива впереди движущегося забоя от его есте­ственной температуры до температуры плавления и на ради­альное рассеивание в окружающем пенетратор массиве (2*.

В рамках принятых допущений количество теплоты в единицу времени на перегрев окружающего пенетратор расплава можно выразить через площадь сечения скважины с учетом толщины слоя расплава в верхней части пенетратора 26 (при средней его тол­щине 6), температуру расплава как среднюю арифметическую между температурой поверхности пенетратора и температурой плавления породы /агр и установившуюся скорость бурения V.

<?1 = у Я (Я + 2б)2 С«Рж (*н — ^агр) V, (5.52)

где /? — радиус верхнего торца пенетратора, м; 6— средняя тол­щина слоя расплава под пенетратором, м; сж — удельная массо­вая теплоемкость расплава, Дж/(кг-°С); рж — плотность расплава, кг/м3; tн — средняя температура рабочей поверхности пенетра­тора, °С; /агр — температура плавления породы (агрегатного пере­хода), °С; V — установившаяся скорость бурения плавлением, м/с.

Из тех же соображений тепловой поток на плавление горной

«ороды выразим соотношением

(?2 = л (/? + 26)2 ‘фрта, (5.53)

где ф — скрытая теплота плавления породы, Дж/кг; рт — плот­ность горной породы, Дж/(кг-°С).

Количество теплоты, рассеивающееся в единицу времени в ок­ружающем пенетратор горном массиве, в соответствии с упомяну­тым выше принципом элементарной суперпозиции [37] будем рас­сматривать раздельно для осевого и радиального направлений, предварительно представив реальный пенетратор в виде эквива­лентного ему по объему цилиндра радиусом /?. При этом прини­мается, что в осевом направлении тепловой поток распростра — ияется по площади поперечного сечения скважины — п(/? + 26)2, а в радиальном направлении — по ее боковой поверхности пло: щадью 2л (/? + б)Яц.

В работе [23] на основе методики движущегося теплового ис­точника [81] показано, что температурное поле впереди плоского забоя (одномерная задача) в условиях установившегося процесса бурения плавлением описывается выражением

V

{ = *т + ^е “Л (5.54)

где и — естественная температура породы на данной глубине, °С; q — поверхностная плотность теплового потока, Вт/м2; ат — тем­пературопроводность породы, м2/с; Ят — теплопроводность породы; Вт/(м-°С); 2 — координата в движущейся системе координат, совпадающая с осью х, параллельно которой движется плоский источник тепла, м.

Полагая для поверхности забоя 2=0, ^ = ^агр и раскрывая а,- = },г/ (Стр.,.), для количества теплоты в единицу времени на

прогрев породы от температуры плавления впереди движущегося

забоя с учетом оплавления стенок скважины на основе выражения

(5.54) после преобразований получим

<2з = л (/? + 26)2 стрт (*агр — /т) V. (5.55)

Для оценки теплового потока в окружающий массив в радиаль­ном направлении от пенетратора в соответствии с изложенными выше допущениями примем за основу известное выражение (см., например, [37]) для количества теплоты, поступающей в полуог- раниченное тело за время т, которое применительно к нашему слу­чаю представим в виде

0 = 2/> д/(/агр — *т) ут, (5.56)

где /V — площадь поверхности полуограниченного тела, м2; К — теплопроводность горной породы, Вт/(м-°С); т — продолжитель­ность теплового воздействия боковой поверхности пенетратора на окружающий массив, с.

Среднее значение теплового потока на радиальное рассеивание можно оценить как среднее за время т количество теплоты, погло­щаемой окружающим массивом:

<2* = 0/г. (5.57)

Представляя в соответствии с принципом элементарной супер­позиции действительный пенетратор в виде эквивалентного ему по объему цилиндра радиусом /?, площадь поверхности полуограни­ченного тела с учетом средней толщины слоя расплава б можно выразить следующим образом:

/> = МЯ-М)Яц, (5.58)

где Нц—-высота цилиндра радиусом /?, эквивалентного действи­тельному пенетратору по объему, м.

Время воздействия высокотемпературного пенетратора на ок­ружающий массив в радиальном направлении можно выразить че­рез высоту эквивалентного цилиндра и скорость бурения плавле­нием:

т = Нг/ю. (5.59)

Подставив соотношения (5.58) и (5.59) в равенство (5.56) и затем в выражение (5.57), после преобразований для теплового потока на радиальное рассеивание в окружающем пенетратор мас­сиве получим

— 4 (Я + 6) Уя/,тСтртЯц£> (/шр — /т). (5.60)

Решая тепловой баланс

Л^а = С1 + (^2 + 0з + С?4 (5.61)

2(ЛГа

+

агр + 0^ — (Зз ~~ <3«)

п (Я + 26)2 сжржи

Рис. 5.6. Профиль пеиетратора в форме тела вращения цепной ли­нии. а — параметры цепной линии; б —изме­нение профиля пенетратора в зависи­мости от его высоты при постоянном диаметре торца.

относительно средней тем­пературы поверхности пене — тратора и, получаем урав­нение

(5.62)

в правую часть которого входит неизвестная величина — скорость бурения плавлением.

Вместе с тем для теплового потока от общей рабочей поверх­ности пенетратора Т7 с температурой /н в окружающий массив че­рез слой расплава средней толщиной б справедливо выражение

(5.63)

приравняв которое К сумме <32, (28 И <^4 и решив относительно

и, получим второе уравнение для средней температуры поверх­ности пенетратора

6 № — Ь Яз ~Ь Я*)

агр

(5.64)

в правую часть которого помимо искомой установившейся ско­рости бурения V входит неизвестная средняя толщина слоя рас­плава б.

Толщина слоя расплава под пенетратором определяется суммой гидродинамического и гидростатического давлений, испытываемых расплавом при выдавливании, и зависит от плотности и вязко­стных свойств расплава при средней температуре, от осевой на­грузки на пенетратор и скорости бурения плавлением.

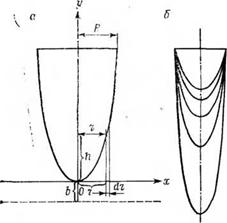
Примем во внимание геометрические особенности пенетратора в форме тела вращения цепной линии вокруг вертикальной оси /рис. 5.6). Легко показать, что если параметр цепной линии Ь при­нят за единицу масштаба, профиль осевого сечения пенетратора

‘[(зависимость его высоты к от радиуса г) выражается соотноше­

нием

к = Ь сЬ (г/Ь) — Ь, (5.65)

длина дуги профиля
площадь рабочей поверхности пенетратора

Я = 2лЬ [Я (Я/Ь) — Ь сЬ (Я/Ь) + Ь), (5.67)

объем пенетратора

V = лЬ [(/?2 + 2Ь2) сН (Я/Ь) — 2ЬЯ эИ (Я/Ь) — 2Ь2]. (5.68)

Выражения (5.65) — (5.68) необходимы в дальнейшем для рас­четного анализа.

Гидродинамическое и гидростатическое давления в слое, рас­плава в направлении от нижней части пенетратора к его верхнему торцу снижаются, что в дифференциальной форме с учетом закона Дарси — Вейсбаха можно записать в виде

йр = —К ™2а’К ^— ёРж(Мг. (5.69)

Переменная по высоте пенетратора скорость движения рас­плава определяется отношением его объема №’ = лг2^, образую­щегося в единицу времени, к площади сечения кольцевого канала на данной высоте / = 2яг6, в силу чего

да = -|—£-и. (5.70)

При условно принятой постоянной средней толщине слоя рас­плава эквивалентный диаметр кольцевого канала на любой вы­соте

4 = 26. (5.71)

С помощью выражений (5.65), (5.66), (5.70) и (5.71) преобра­зуем дифференциальное уравнение (5.69) к виду

с1р = — ^зж г2 СЬ (Г/Ь) (1г — gpж бЬ (г/Ь) с1г. (5.69а)

Интегрируя левую часть уравнения (5.69а) в пределах от р до 0 и правую — от г — 0 до конечного радиуса пенетратора Я (верхний торец), находим

Р = Ь [(Я2 + 2Ь2) зЬ (Я/Ь) — 2ЬЯ сИ (Я/Ь)] + ёЬРж [сЬ (Я/Ь) — I ].

(5.72)

Принимая в порядке первого приближения половинное значе­ние давления р для некоторой средней толщины слоя расплава 6, на основании выражения (5.72) получаем

1 з/ху2ржЬ[{Я2 + 2Ь2)&ЪШЬ)_2ЬКсЬ(Р,/ь-^

2 У 2{2Р-£РжМсЬ(Я/г>)-П} ’

где в правую часть входит неизвестная величина — скорость буре­ния плавлением.

Мы имеем теперь три уравнения (5.62), (5.64) и (5.73) с тремя неизвестными: V — скорость бурения плавлением; и — средняя тем­пература рабочей поверхности пенетратора и б — средняя
толщина слоя расплава. В результате совместного их решения по­лучим приближенное аналитическое выражение для зависимости скорости бурения плавлением от основных конструктивных. и тех­нологических параметров в виде следующего трансцендентного уравнения:

3/ Ла2ржЬ [(№ ‘+ 262) 8Ь (Я/6) — 2Ы* сЬ (И/Ь) / 2 {‘2р — држ6 [сЬ (/?/&)-!]}

зі (Я + 26)2 в [л(« + 26)2 (ф + ст Д<) ртр + 4 (Я + 6) Ы УлЛтстртЯцг

(5.74)

где У7 — общая рабочая поверхность пенетратора, м2; аж — коэф­фициент температуропроводности расплава, м2/с; — радиус верх­

него торца пенетратора, м; и — скорость бурения плавлением, м/с; УУа — активная мощность пенетратора, Вт; ф — удельная теплота плавления породы, Дж/кг; ст — удельная массовая теплоемкость породы, Дж/(кг-°С); М — разность между температурой плавле­ния и естественной температурой породы, °С; А, т — коэффициент теплопроводности породы, Вт/(м-°С); рт и рж — плотность породы и расплава соответственно, кг/м3; НА — высота эквивалентного цилиндра, м; % — коэффициент гидравлического сопротивления при движении расплава; Ь — параметр цепной линии, м; р — удельная осевая нагрузка, Па; g—ускорение свободного падения, м/с2.

Полученное уравнение скорости бурения плавлением связывает между собой все основные определяющие процесс факторы: кон­структивные параметры пенетратора, его активную тепловую мощ­ность, осевую нагрузку на забой, а также теплофизические свой­ства’ проходимой породы и ее расплава.

Если для конкретных условий с помощью уравнения (5.74) вычислить значение скорости бурения плавлением V, то подставив его в выражение (5.73), можно определить расчетным путем та­кую важную характеристику процесса, как средняя толщина слоя расплава под пенетратором 6.

Формулы (5.62) и (5.64), если раскрыть входящие в них част­ные тепловые ПОТОКИ С^2, (?з И <24 с помощью выражений (5.53),

(5.55) и (5.60), позволяют получить две независимые формулы для оценки средней температуры поверхности пенетратора при за­ранее вычисленных для конкретных условий значениях и и б. Эти формулы соответственно имеют вид

(5.75)

2 [Лґа — я (Я + 26)2 (і]) + ст Д<) ртг — — 4 (Я + 6) Д< VЭТЯчСтрт//ц1,’]

и

+

6 [я (Я + 26)2 (ф + ст ДО ртУ + 4 (я + 6) М УяЛтстртЯци ]

ЬжР

Здесь обозначения аналогичны принятым выше.

При подстановке в формулы (5.75) и (5.76) правильно вычис­ленных для конкретных условий значений V и 6, обе формулы должны дать одинаковый результат. Помимо определения ценного для характеристики процесса значения средней температуры по­верхности пенетратора іи факт совпадения расчетов по формулам

(5.75) и (5.76) может свидетельствовать о достоверности вычис­ленных значений скорости бурения плавлением V и средней тол­щины слоя расплава б, что должно быть использовано для кон­троля точности расчетов.

Комментарии запрещены.