Расчетный анализ
Расчетный анализ
Расчеты выполнены на отечественном персональном компьютере типа ДВК-ЗМ2 по специально разработанной программе и представлены графически на рис. 5.9—5.14.
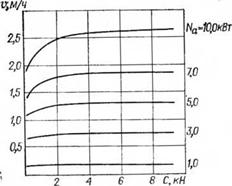
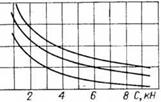
Графики на рис. 5.9 показывают, что скорость бурения плавлением по базальту практически прямо пропорциональна активной тепловой мощности пенетратора и в существенно меньшей степени зависит от осевой нагрузки. Последняя сказывается лишь при малых значениях (до 2—4 кН), но в тем большей мере, чем выше активная мощность пенетратора. Так, если при — 1 кВт кривая зависимости v = f(C) практически параллельна оси абсцисс, то при Л/’а = 5 кВт она вынолаживается при С> 4 кН.
Из теории следует, что скорость бурения плавлением в общем случае пропорциональна корню третьей степени из удельной осевой нагрузки. С увеличением осевой нагрузки снижается толщина слоя расплава под пенетратором, что подтверждают данные рис. 5.12. Но увеличение скорости бурения плавлением за счет лучшей теплопередачи влечет увеличение количества расплава в единицу времени, что в условиях суженного канала ведет к резкому возрастанию гидравлических потерь давления, в силу чего кривые V — }(С) быстро выполаживаются.
Увеличение осевой нагрузки на пенетратор в условиях рассматриваемого примера даже при А^а = 5 кВт выше 4—5 кН не имеет смысла. Осевую нагрузку нельзя рассматривать как серьезный резерв повышения скоростей бурения горных пород плавлением, тем более если используется буровой снаряд на грузонесу — щем кабеле или шлангокабеле.
|
1Т, М/Ч Рис. 5.10. Расчетные графики зависимости скорости бурения плавлением V по базальту от высоты Я пенетратора (I) = 50 мм) при различных значениях активной мощности Д’а. |
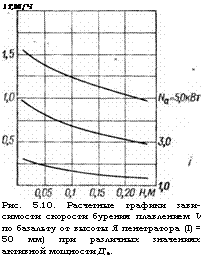 На рис. 5.10 наглядно иллюстрируется отрицательное влияние излишней высоты пенетратора. При этом темп снижения скорости бурения плавлением тем выше, чем больше фиксированная активная мощность пенетратора. Причина в том, что при постоянной мощности пропорционально высоте пенетратора возрастает бес-
На рис. 5.10 наглядно иллюстрируется отрицательное влияние излишней высоты пенетратора. При этом темп снижения скорости бурения плавлением тем выше, чем больше фиксированная активная мощность пенетратора. Причина в том, что при постоянной мощности пропорционально высоте пенетратора возрастает бес-
|
Рис. 5.9. Расчетные графики зависимости скорости бурения плавлением V по базальту пенетратором (О = = 50 мм, // = 75 мм) от осевой нагрузки С при различных значениях активной мощности Д’а. |
|
|
|
|
|
|
|
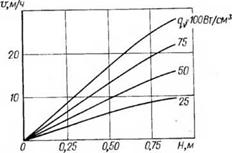
Рис. 5.14. Расчетные графики зависимости скорости бурения плавлением V по базальту от высоты пене — тратора (£> = 50 мм) при осевой нагрузке С = 5 кН и различных значениях удельной объемной мощности |

|
и-3,0м/ч |
![]()
|
О Ц5 10 1,5 V, 1б3М2/с |

|
Рис. 5.13. Расчетные графики зависимости средней толщины слоя расплава горной породы 6 (пенетратор (Д = 50 мм, Я = 75 мм) от его вязкости V при различных значениях скорости бурения плавлением V как функции активной тепловой мощности N а. |
полезное рассеивание теплоты в массиве в радиальном направлении.
В полном соответствии с теорией скорость бурения плавлением тем выше, чем меньше высота пенетратора, но при этом пропорционально снижается полезный объем для размещения внутри пенетратора электросопротивления достаточной мощности. В этом противоречии заключается задача оценки оптимальной высоты и энерговооруженности пенетратора.
На рис. 5.11 показана расчетная зависимость скорости бурения плавлением от теплопроводности породы. Естественно, что с увеличением последней растут нерациональные потери теплоты на рассеивание в массиве, и скорость бурения падает.
На рис. 5.12 демонстрируется снижение средней толщины слоя расплава под пенетратором с ростом осевой нагрузки. По абсолютной величине толщина слоя расплава при любой нагрузке
практически прямо пропорциональна активной тепловой мощности, поскольку в той же пропорции возрастает количество образующегося в единицу времени расплава. Характерно, что при любой активной мощности кривые б — f(C) стремятся к постоянным минимальным значениям; это подтверждает справедливость соображений, высказанных относительно влияния осевой нагрузки на скорость бурения плавлением (см. рис. 5.9).
Поскольку гидравлические потери давления при выдавливании расплава существенно зависят от его вязкости, средняя толщина слоя расплава возрастает с увеличением последней, и в тем большей мере, чем выше скорость бурения как функция активной мощности пенетратора, что показывают на рис. 5.13 кривые зависимости б = f(v) при разных значениях скорости и. По характеру этих кривых можно судить, что они также выполаживаются с ростом вязкости, но на разных уровнях, зависящих от скорости бурения плавлением. Причем различия в средней толщине слоя расплава при разных скоростях бурения тем больше, чем выше вязкость расплава, поскольку с ростом последней увеличиваются гидравлические потери давления.
На рис. 5.14 показаны расчетные зависимости скорости бурения плавлением по базальту от высоты пенетратора в условиях пропорционального возрастания его активной тепловой мощности при разных значениях удельной объемной мощности qv. Графики показывают прямое пропорциональное возрастание скорости бурения плавлением с ростом высоты пенетратора до 0,5—0,6 м, после чего темп прироста скорости начинает снижаться, и тем быстрее, чем выше удельная объемная мощность. Дело в том, что, несмотря на возрастание суммарной тепловой мощности пенетратора, с ростом его высоты увеличиваются гидравлические сопротивления при выдавливании расплава, возрастает средняя толщина слоя расплава и, главное увеличивается доля теплоты на бесполезное радиальное рассеивание в окружающем массиве.
Из теоретических соображений и характера кривых на рис. 5.14 можно сделать вывод о наличии максимума скорости при любой (удельной) объемной мощности, после чего должно происходить снижение скорости бурения плавлением. Более того, в настоящей методике расчетов не рассматривается появление при определенной высоте пенетратора естественной конвекции расплава в условиях увеличивающейся толщины его слоя б и, следовательно, тур — булизации потока, влекущей повышение интенсивности теплопередачи с боковой поверхности. Кроме того, как можно показать расчетом с помощью формул (5.75) или (5.76), с увеличением высоты Я при qv = const резко возрастает средняя температура поверхности пенетратора, и по этой причине не исключено кипение расплава. В силу фазового перехода многократно возрастает теплоотдача с боковой поверхности пенетратора, и дальнейшее увеличение его высоты и мощности лишено смысла.
Вместе с тем графики на рис. 5.14 показывают принципиальную возможность достижения высоких скоростей бурения горных пород плавлением—15—20 м/ч. Главная проблема заключается в обеспечении достаточно высокой жаропрочности конструкционных материалов. Как легко показать аналитически и с помощью расчетов, температура в центральной части теплового пенетра — тора, т. е. температура источника тепловой энергии — элемента электросопротивления, в процессе бурения горных пород плавлением может на сотни градусов превышать температуру рабочей поверхности пенетратора, что зависит от теплофизических свойств материала его корпуса.
Современные успехи в разработке новых жаропрочных конструкционных материалов позволяют надеяться на реальность создания долговечных и высокопроизводительных тепловых пене- траторов для бурения горных пород плавлением.