Бурение грунтовых зондов, установка энергетических колодцев

Особо важную роль тепло — и массообменные процессы при­обретают при бурении скважин в многолетнемерзлых породах, ко­торые распространены приблизительно на половине территории СССР [23, 30, 38, 44]. Высокая чувствительность сцементирован­ных льдом рыхлых отложений и разрушенных коренных скаль­ных пород к нарушению их температурного и агрегатного состоя­ния, влияние аккумулированного горными породами холода на устойчивость ствола скважины и протекающие в нем процессы яв­ляются причинами частых, разнообразных по природе и тяжелых по последствиям осложнений.

Главной причиной этих осложнений является недоучет темпе­ратурного фактора, нарушение нормального температурного ре­жима скважины, при котором интенсивность теплообменных про­цессов между мерзлыми породами и циркулирующей в скважине промывочной средой, оставаясь в допустимых пределах, не вызы­вает нарушения агрегатного состояния льда как связующего це­мента. Примерами неверного подхода в этом вопросе являются известные в практике попытки применять нагретую воду или гли­нистый раствор в целях борьбы с образованием шуги, ледяных пробок, намерзанием сальников и т. п., что приводило к наруше­нию связности сцементированных льдом пород и их обрушению, обвалам и тяжелым авариям. Эффективнее оказалось применение солевых и подсоленных глинистых растворов, но и в этих случаях осложнения не устранялись полностью из-за недоучета влияния положительной температуры раствора и растворяющего действия соли на лед [23, 24, 30, 44].

Возможность искусственного регулирования температуры в стволе бурящейся скважины зависит от физических и теплофизи­ческих свойств промывочной среды. Замена замерзающей при 0°С воды незамерзающими при естественной температуре мерз­лых пород (до —15°С) достаточно концентрированными раство­рами ЫаС1 или СаС12, растворами на углеводородной основе или воздухом еще не решает задачи, не обеспечивает нормального тем­пературного режима скважины при бурении в мерзлоте. Даже охлаждение той или иной незамерзающей промывочной среды на поверхности до отрицательных температур не всегда гарантирует от осложнений и аварий без знания закономерностей теплообмен­ных процессов в стволе бурящейся скважины, характера распре­деления температуры по глубине. Температура жидкой или газо­образной промывочной среды различна в каждой точке циркуля­ционной системы скважины, является результатом нестационар­ного (зависящего от времени, продолжительности процесса) теплообмена между окружающим скважину массивом мерзлых или «морозных» пород и циркулирующей в скважине промывоч­ной среды и зависит от физических и теплофизических свойств по­следней.

Частые и разнообразные по природе осложнения, связанные с высокой чувствительностью мерзлых пород к нарушению их тем­пературного режима и агрегатного состояния содержащейся в них влаги, требуют детального изучения и учета температурного фак­тора при выборе технических средств и разработке рациональной технологии бурения как сравнительно неглубоких разведочных, гидрогеологических и инженерно-геологических скважин, так и глубоких скважин на нефть и газ.

В соответствии со спецификой протекания тепло — и массооб­менных процессов при бурении скважин в мерзлых породах рас­смотрим следующую упрощенную постановку задачи о ее темпе­ратурном режиме.

Пусть температура циркулирующего в кольцевом канале сква­жины потока промывочной среды будет выше температуры агре­гатного перехода содержащегося в мерзлых породах льда ^,гр, т. е. Ь > ^агр — Тогда в результате теплового взаимодействия потока про­мывочной среды с массивом мерзлых пород в процессе бурения вокруг ствола скважины будет образовываться зона талых пород радиусом Гагр’Ог, т), т. е. область с температурой горных пород Ат ^ ^агр. толщина которой будет зависеть от теплофизических свойств горных пород, интенсивности и времени теплового взаи­модействия и от глубины рассматриваемого интервала скважины.

Так как температура мерзлых пород, как правило, ниже тем­пературы замерзания (протаивания) содержащейся в них влаги, то образование зоны талых пород вокруг скважины начнется тогда, когда температура на ее стенке станет равной taтp, т. е.

1г==я0 = ^агр-

Таким образом, задача о температурном режиме скважины при бурении в мерзлых породах может быть разделена на две вполне самостоятельные задачи. Первая задача характеризуется тем, что температура на стенке скважины не превышает темпера­туры протаивания мерзлых пород, и теплообмен последних с по­током циркулирующей среды происходит без агрегатного пере­хода лед — вода. Вторая задача сводится к определению темпера­турных полей в потоках промывочной среды и в горных породах, когда вокруг скважины начинают образовываться две зоны — та­лая и мерзлая — с подвижной границей между ними гагР(г, т).

Первая задача аналогична ранее рассмотренной задаче о тем­пературном режиме бурящейся скважины до периода времени от то до Тагр, за который температура пород на стенке скважины

достигнет температуры агрегатного перехода tягp. Для этого слу­чая температурные поля в восходящем и нисходящем потоках £2 и Л можно рассчитать по методике, рассмотренной в разделе 1.3.

Температурное поле в окружающем скважину мерзлом мас­сиве при отсутствии в последнем фазовых (агрегатных) изменений может быть определено из решения задачи о переносе тепла в гор­ных породах. Для скважины при < Я можно пренебречь в окружающих горных породах переносом тепла вдоль оси г, и тогда задача о распределении температуры в горных породах может быть упрощена и сформулирована в следующем виде:

TOC o "1-5" h z -^- = «пТ—|г(»-^!-) для /?0<г < °о и т0<т<тагр (2.1)

с начальными и граничными условиями

а) т = т0, /„ = /„()(/-, т0);

б) г — /?0» К д^дх = «2 (/„ — 4); (2.2)

в)г = оо, Нщ (/„ — /п0) -> 0.

Исследование задачи (2.1) с условиями (2.2) было проведено в работе [40]. Предполагаемое решение отыскивалось в виде

— ^по (г, То + т) + II (г, т). (2.3)

После перехода к безразмерным параметрам Ро=апт//?2, /? =

= г/Я0, В1 == а2/?0/Яп задача (2.1) — (2.2) путем подстановки в нее выражения (2.3) была преобразована к следующему виду:

для 0<Ро<Роагр (2.4)

с начальными и граничными условиями

а) Ро = 0, и = 0;

б) /? = 1, ди/дЯ = В1 [и- и о (Ро)]; (2.5)

в) /?—» сю, и0.

Здесь

Яц^агр ^°агр “ Гг •

"о

С помощью метода интегральных соотношений в работе [40] было получено приближенное решение задачи (2.4) с условиями (2.5) в виде

гп(Я, Ро) = /п0 + (*2-/п0) °-^ПпТ(Щ" для »(2-6)

где 1{¥о)=гвоз/Я0 — безразмерная граница возмущенной зоны ра­диуса Гвоз, т. е. граница области, где произошли температурные изменения в породе.

Для определения 1(Ро) б той же работе предлагается следую­щая зависимость:

р°=тНлтЩгн-В1,!(1)}’ (2’7)

где

/, = 1п / (Ро) + -35т;

Г /2(Ро) , Г. ,/с ч I 1 Л. В12-2В1 + 2

/2 = — У^ + [1П/(Р0)+ ВТ ~ 1 +——————————- 4ВР——— *

Ввиду того что для сохранения связности и устойчивости сце­ментированных льдом мерзлых пород, обеспечивающих нормаль­ный процесс бурения скважин, необходимо, чтобы ни на одном из участков ее ствола температура пород на стенке не превышала температуры агрегатного перехода лед — вода, с практической точки зрения особую важность приобретает определение момента времени Роагр, после которого возможно начало процесса измене­ния агрегатного состояния мерзлых пород. Для того чтобы найти время Роагр, положим в уравнении (2.6) ^п|к=1 = ^агр. Тогда, счи­тая /агр = 0°С, получаем

В1 1п I (Роагр)

0 = ^0 + (*2- и Т+йПЩ — (2.8)

или после преобразований

/(Роагр) = ехр(-1^г), (2.9)

где /(Роагр) — безразмерная граница возмущенной температурной зоны в породах вокруг скважины на момент времени Роагр, когда на стенке скважины температура достигает 0°С.

Подставляя выражение (2.9) в уравнение (2.7), находим

р0агр=кг[тПм-В1^(1)]- ^2’10^

Таким образом, с помощью выражений (2.9) и (2.10) мы мо­жем определить момент времени Роагр, соответствующий установ­лению на стенке скважины при бурении температуры 0°С.

После достижения этого момента начинается процесс измене­ния агрегатного состояния содержащегося в породе льда, и тем­пературный режим в скважине будет определяться решением вто­рой задачи. Следует отметить, что, так как /(Роагр) = Д^г), а зависит от глубины скважины, т. е. в нашем случае от ее безраз­мерной координаты X = гЩ, значение безразмерного времени Роагр будет зависеть от координаты Z. Следовательно, процесс агрегатного перехода в мерзлых породах по глубине скважины будет начинаться в разные моменты времени.

Для решения второй задачи, связанной с определением темпе­ратурного режима скважины в условиях происходящих в окру­жающих ее мерзлых породах агрегатных изменений, восполь­зуемся понятием об интенсификации теплообмена при агрегатном

переходе влаги, содержащейся в горных породах &агр. Этот коэф­фициент впервые был предложен Ю. Д. Дядькиным [23] для приближенных расчетов температурных полей в горных выработ­ках и успешно применен для решения аналогичных задач при бу­рении скважин [23, 24]. Для условий нестационарного теплооб­мена, сопровождающегося процессами промерзания или протаи — вания горных пород, в работе [40] предлагается использовать коэффициент нестационарного теплообмена при наличии в поро­дах агрегатных переходов &та, который удобно записать в следую­щем виде:

Къ = КтрК (2.11>

Таким образом, с физической точки зрения коэффициент теп­лопередачи &та учитывает изменение количества теплоты на агре­гатный переход влаги в связи с продвижением границы оттаива­ния мерзлых пород, окружающих в данном интервале ствол сква­жины, и на увеличение теплосодержания окружающих скважину пород, т. е. увеличение температуры последних. Наличие агрегат­ного перехода в окружающих скважину породах существенно сни­жает границы зоны с возмущенной (измененной) температурой, особенно в начальные моменты времени. Это приводит к умень­шению теплового сопротивления этой зоны при теплообмене цир­кулирующего в кольцевом канале очистного агента с окружающим горным массивом и тем самым повышает коэффициент теплопере­дачи, т. е. ^агр^1. В случае, когда теплообмен протекает без агрегатных переходов, /гагр = 1, а Л« = кх.

В условиях изменения агрегатного состояния влаги в горных породах при бурении скважины связь между температурой ее стенки и температурой промывочной среды в кольцевом канале с использованием понятия о коэффициенте нестационарного тепло­обмена при агрегатных переходах можно записать по анало­гии с выражением (1.48) в безразмерном виде:

©п1^1=(1—^)©2. (2:12)

С помощью коэффициента &га выразим тепловой поток на стенке скважины в случае квазистационарного режима теплооб­мена между промывочной средой в кольцевом канале скважины и массивом мерзлых пород в виде следующей зависимости:

Я = (2.13)

Кроме того, тепловой поток на стенке скважины со стороны массива горных пород может быть определен равенством

*=тг*.4Н_».- (214>

Приравнивая (2.13) и (2.14), находим выражение для опреде­ления кха в следующем виде:

с 1 II	0

^2

(2.15)

Итак, вторая задача по определению температурных полей мо­жет быть сформулирована аналогично первой задаче с заменой на &та. Следовательно, вся сложность второй задачи формально сведена к определению 6га, а с учетом выражения (2.15)—к опре­делению температурного поля в окружающем скважину массиве мерзлых пород.

Задача о температурном поле в горных породах с уче­том происходящих в них фазовых превращений для мо­мента времени т > Гагр может быть сформулирована следующим образом:

	1	д
—2- = а+	«—-	_____
дх п	Г	дг
	1	д
д% п	г	аГ

т

я0<г<гап> (т); Гагр М < Г < 00

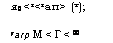
(2.16)

с начальными и граничными условиями

а) т = тагр, *п=/п0(г),

(2.17)

б) г=я0, к^г=^ал-(2у,

в) г = гагр (т), tn = гагр, С + Яп ~~ = Ч’у

г) г-> оо, /п0 = 0.

Здесь индексы «-)-» и «—» относят значения соответствующих им характеристик соответственно к немерзлым и мерзлым породам. В условии «а» функция £п0 определяется решением первой задачи для момента времени т = тагр и при А = ^агр (для случая оттаи­вания мерзлых пород /агр = 0°С). Условие «в» подобно условию Стефана на границе раздела талой и мерзлой зон в породе, где Ч’у— объемная теплота агрегатного перехода.

Следует отметить, что задача (2.16) с условиями (2.17) яв­ляется частным случаем рассмотренной нами выше задачи (1.43) —

(1.44).

Для получения простых расчетных зависимостей воспользуемся приближенным решением поставленной задачи, найденным в ра­боте [40].

При Ро > РОагр

. В1 1п (1ггр/К)

*« =*» г+в ап-‘ 1 <2-18)

* Г, , Я2 — Ь* — 2Ь1п (ЩЦ 1

/. гр<Я<1; (2.19)

£ = 4Г РУ^; (2.20)

TOC o "1-5" h z Ге*р(*), *>0; _Л_. (221)

агр (1, *<0; гКо + Мпо/^!/7^) В!’

—

? 1 (‘агр) ^ПО 4 и

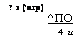В1 /2(1) + Ко (^■■12-а,|) + — — Ц=1) +

+

I [^. (2) А (/агр) — т7, (г0) + Р2 (г) — Р2 (^о)] =

= (1 + I *по/*21) (Ро — Роагр). (2.22)

В этих выражениях

г /, ^ ‘аго (, . 1 Л В12—2В1 +2

TOC o "1-5" h z Ы^гр)—————— ^ агрН — 1)н—————————————- 4в]———— ;

11 (^агр) 1п ^агр Н •

р (7 У-1)2 .

Г\^) -Z—ZrZ’

р 2221п2-522 + 8^-3

4(1 _ г + гпг) :

Ко = ^ ^0.

Проведенный анализ этого приближенного решения позволяет для случая квазистационарного режима определять коэффициент нестационарного теплообмена с учетом изменения агрегатного со­стояния горных пород

йта=ТТсгЬ————— (2.23)

та 1 + В1 1п /агр ‘

и коэффициент интенсификации теплообмена при агрегатном пе­реходе

, _ 1 + В1 1п(1 + У2Ро) /9 94^

«агр 1 + В! 1п /агр ’ К )

Более простое выражение для определения безрамерной вели­чины зоны изменения агрегатного состояния мерзлых пород во­круг скважины /агр получено в работе [40] при решении задачи (2.7) для талой зоны методом интегральных соотношений при условии, что начальная температура пород близка к температуре
агрегатного перехода содержащейся в ней влаги, в следующем виде:

’Р (I2 In / /2 — 1 /2 — і Л

Р ______ _ х у | ‘агр 111 ‘агр ■ ‘агр 1______ ‘агр 1 1 _

° Спрп^2 V 2 ‘ 2ВІ 4 /

Bi f’arp“1 ‘агр“1 , ІП, агр ІП ‘агр ^

l + Biln;arpV 4 ВІ 4 + 4 2 Bi )

(2.25)

Для удобства практического использования расчетной зависи­мости (2.25) необходимо границу оттаявшей зоны в мерзлых поро­дах считать параметром и для каждого его значения определять соответствующие значения температуры промывочной среды в кольцевом канале скважины при фиксированных значениях вре­мени циркуляции Ио или наоборот.

Анализ выражений (2.15), (2.24) и (2.25) показывает, что в общем случае коэффициент &та является функцией многих пара­метров, так как зависит от времени, от начальной температуры пород, температуры промывочной среды в скважине, теплофизи­ческих характеристик пород, от критерия Ві. Как показал анализ, выполненный в работе [40], для практических расчетов исполь­зование а возможно во всех случаях, когда соблюдается условие

912 91 агр ^ ! (2.26)

dl агр dZ

т. е. когда температура промывочной среды в кольцевом канале незначительно меняется с перемещением границы фронта оттаи­вания мерзлых пород вокруг скважины и изменение этой границы по глубине скважины также незначительно. Первое условие прак­тически всегда выполняется при бурении разведочных скважин глубиной до нескольких сотен метров, что отвечает реальным глу­бинам распространения мерзлых горных пород для большинства геологических разрезов. Второе условие иногда может не выпол­няться, особенно при нарушении технологического режима буре­ния в мерзлых породах, связанном с использованием промывоч­ных агентов с высокими положительными температурами. Однако для нормализованных условий бурения и это условие должно со­блюдаться. Поэтому использование коэффициента теплопередачи кха для практических расчетов температурного режима скважины при бурении мерзлых пород вполне правомочно.

Для расчета температурного режима скважины при бурении в мерзлых породах с учетом возможного растепления ее стенок на отдельных интервалах (устье, призабойная зона) или по всему стволу воспользуемся полученными в разделе 1.3 приближенными выражениями для распределения температуры промывочной среды в канале бурильных труб ^ (1.55) и в кольцевом затрубном про­странстве ^2 (1.56). Влияние агрегатных изменений в мерзлых по­родах на температуру промывочной среды будет учитываться при вычислении корней характеристического уравнения и Бч для определения переменных значений векторов X,, Х2, У1 и У2. Для

этого kx в характеристическом уравнении нужно заменить на kxa> вычисляемый по формуле (2.23).

Так как /аГр в общем виде зависит от времени циркуляции и глубины скважины, решение второй задачи представим в виде

U (X, Fo) — f„X, (X, /агр) + At3Y, (X, /агр); (2.27)

h СX, Fo) = tH2 (X, /агр) + At3Y2 (X, Zarp). (2.28)

Для определения /агр можно использовать точное выражение

<2.21) или приближенное (2.25). Если нужны точные расчеты, сле­

дует использовать описанный ниже алгоритм вычислений по фор­мулам (2.27) и (2.28).

1. Задается параметрически граница фронта оттаивания мерз­лых пород /агр в необходимом по глубине скважины сечении, опре­деляемом координатой Z = z/H.

2. По формуле (2.23) вычисляется соответствующий заданному ЗНаЧеНИЮ /агр коэффициент нестационарного теплообмена с учетом агрегатных изменений, происходящих в мерзлых породах.

3. С помощью выражений (2.27) и (2.28) определяется темпе­ратура циркулирующей промывочной среды в заданном сечении и при заданном положении границы раздела фаз.

4. Из выражения (2.25), имея значения /агр и h для данного сечения, определяем время, которому соответствует заданная гра­ница оттаявшей области в мерзлых породах и определенная уже нами температура промывочной среды.

Для реализации этого алгоритма разработана программа в ре­жиме диалога на языке BASIC для персональных ЭВМ IBM РС-ХТ, а также совместимых с ними отечественных ЕС-1842, «ИСКРА-1030-11».

Для приближенных практических расчетов этот алгоритм мож­но значительно упростить, используя при определении багр другие, менее сложные методы.

Так, для определения значений karp в конкретных условиях проветривания горных выработок Ю. Д. Дядькиным [23] пред­ложена приближенная (не учитывающая длительности циркуля­ции Fo) формула

&агр = 1 + K^tcn ‘ (2-29)

где Wп — активная массовая влажность породы (отношение массы льда или свободной воды в единице объема мерзлой или немерз­лой породы к ее объемной плотности), доли единицы; ф — удель­ная теплота плавления льда (кристаллизации воды), Дж/кг; |/| — абсолютное значение температуры циркулирующей среды, осред- ненное по протяженности расчетного участка и длительности цир­куляции, °С; Kr — безразмерный коэффициент, зависящий от ха­рактера поля температур вокруг цилиндрической выработки.

Применительно к проветриванию подземных горных вырабо­ток в мерзлых породах при постоянной температуре воздуха /(* = 4,8, тогда как при ее сезонных колебаниях Kr = 10.

Поскольку при бурении с продувкой или промывкой темпера­тура нагнетаемой в скважину промывочной среды практически постоянна и не переходит через 0°С, подставим в выражение

(2.29) Кц = 4,8, а также ■ф = 3,34-105 Дж/кг и после численных преобразований для определения &агр в условиях бурения скважин получим приближенную расчетную формулу

(2.30)

Тогда для нахождения &га достаточно £т, определяемый по фор­муле (1.47), умножить на £агр, определяемый из выражения (2.30). В этом случае распределение температуры в скважине можно определять по упрощенным формулам

(2.31) (2.32)

ІЛХ, Ро) = /НХ, (X) + Л/3У| {Х) и(Х, ¥о) = іМХ) + МлЧ2{Х).

Расчет по формулам (2.31) и (2.32) предполагает, что коэф­фициент £агр зависит только от свойств мерзлых горных пород и не зависит от глубины скважины, от интенсивности и длительности теплообменных процессов.

Простым и достаточно полным по учету определяющих факто­ров применительно к случаю бурения скважин в мерзлых породах является решение, полученное ранее в работе [23]. В результате исследования математической модели тепломассообмена в цирку­ляционной системе скважины при бурении в мерзлых породах задача о ее температурном режиме была сведена к решению не­однородного линейного дифференциального уравнения второго по­рядка с постоянными коэффициентами.

Окончательные аналитические выражения для температуры на любой глубине к при конечной в данный момент глубине сква­жины Н представим в данном случае в упрощенном виде (без учета выделения тепла за счет гидравлической работы трения): для нисходящего потока в бурильной колонне

іу = + П]ЄЗД + То _ а ( 0£_ _ (2 33)

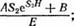
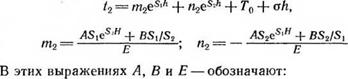
Л = (г1н — То + ^в}, В = а ~ А4; £ = 5^-5^,

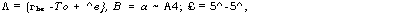
для восходящего потока в кольцевом канале

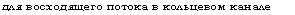
где

(2.34)

где

где корни характеристического уравнения

п (£ £> / £2£>2 Л

2 = Ж 2 ± V 4 + к^°);

^1н — температура промывочной среды, нагнетаемой в бурильные трубы, °С; То — условная постоянная температура поверхности (температура нейтрального слоя), °С; сг— геотермический гра­диент, °С/м; к, Н и О — глубина (текущая координата), конечная глубина и диаметр скважины, м; б и с—массовый расход и удельная теплоемкость промывочной жидкости, кг/с и Дж/(м-°С); Лг’з — прирост температуры промывочной среды у забоя за счет охлаждения работающего породоразрушающего инструмента, °С; к — коэффициент теплопередачи через стенку бурильной колонны, отнесенной к единице длины трубы, Вт/(м-°С); — коэффициент

нестационарного теплообмена, Вт/(м2-°С).

Аналитические выражения (2.33) и (2.34) позволяют опреде­лить температуру в любой системе бурильные трубы — затрубное пространство в любой момент времени от начала циркуляции при известной конечной глубине скважины Н или некотором ее отно­сительном изменении в течение одного рейса Н — Н0— Vт и при­менимы при любом виде промывочной среды (глинистые и другие растворы, вода, воздух, пена) как в случае ее охлаждения при бурении по многолетнемерзлым породам, так и в случае нагрева­ния, например, при глубоком бурении [40].

Для определения по формулам (2.33) и (3.24) температуры промывочной среды при бурении скважины в условиях происходя­щих в мерзлых породах агрегатных превращений влаги при вы­числении корней характеристического уравнения Б2 коэффи­циент нестационарного теплообмена &т умножается на коэффи­циент каГр, определяемый из выражения (2.30). При этом также предполагается, что значение коэффициента /гагр не зависит от глубины скважины и интенсивности и длительнос-ти протекания теплообменных процессов. Однако поскольку смысл анализа теп­лообменных процессов при бурении скважин в мерзлых породах сводится к определению условий, при которых плавление льда — цемента (агрегатное превращение влаги в породах) не будет про­исходить, сложные аналитические построения и расчеты, связан­ные с определением кагр и учетом его влияния на температурное поле в скважине, имеют только теоретическое значение. Важное практическое значение они имеют, например, при анализе темпе­ратурного режима скважины, бурящейся с одновременным замо­раживанием слабосвязных влажных пород за счет циркуляции в стволе низкотемпературной промывочной среды — хладоноси — теля, когда интенсивность теплообменных процессов повышенна за счет кристаллизации влаги в окружающем массиве.

Результаты расчетов, выполненных по рассмотренным трем методикам — формулы (2.27) — (2.28), (2.31) — (2.32), (2.33) —

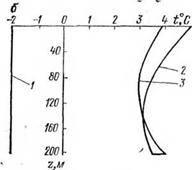
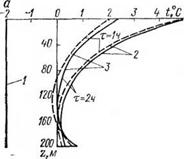Рис. 2.1. Расчетное распределение температуры промывочной среды в бурящейся скважине с учетом (а) и без учета (б) агрегатных переходов.

/ — начальное распределение температуры; 2 — температура в бурильной колонне; 3 —темпера-

тура в затрубном пространстве.

(2.34)—показаны графически на рис. 2.1 и рис. 2.2. Исходные данные для расчетов приведены в табл. 2.1.

Таблица 2.1
Исходные данные для расчета температурного режима скважины, бурящейся в мерзлых породах
1.1	и 2
Ьогр
Показатели Значения Диаметр скважины, м 7,8- 10~2 Внешний диаметр буриль­ 5,0- 10~2 ных труб, м л._______ О Внутренний диаметр бу­ 3,9 ■ 10 2 рильных труб, м Промывочная среда: 4190 с, Дж/(кг • °С) %, Вт/(м • °С) 0,573 а, м2/с 1,37- 10~7 т], Па — с 1,306- НГ3 р, кг/м3 1000 1 О, кг/с *, °С 5 Горные породы: Рп, кг/м3 2000 а~, м /с 6,2- 10~7 а+, м2/с 1,28- 10_6 Я- 2,2 Я+,Вт/(м • °С) 3,1 ■ф, Дж/кг 3,35 • 105 ^агр> С 0 д/з, °С 0,5
Рис. 2.2. Положение границы аг­регатных переходов в мерзлых породах.

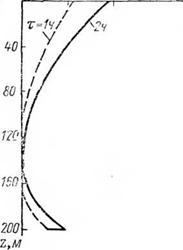
Как видно из графиков, если в качестве очистного агента ис пользуется сжатый воздух, то оттаивание мерзлых пород проис­ходит главным образом в районе устья скважины и в районе за­боя. Этот факт подтверждается и практикой бурения с продувкой в мерзлых породах: образование сальников при бурении, связан­ное с налипанием шлама на оттаявшие стенки скважины, наблю­дается, как правило, в призабойной зоне и в зоне устья скважины. При бурении с использованием в качестве очистного агента жид­кости с положительной температурой растепление стенок сква­жины происходит по всей ее глубине, что также подтверждается практикой бурения скважин в мерзлых породах.

Полное устранение осложнений, связанных с растеплением мерзлоты, возможно в случае, когда ни в одной точке циркуля­ционной системы скважины температура промывочной среды не превышает 0°С. Как показал расчетный анализ [23, 24], даже в случае бурения с продувкой охлажденным до отрицательных температур сжатым воздухом не исключена его положительная температура в призабойной зоне за счет теплоты, выделяющейся при работе породоразрушающего инструмента. Однако при доста­точно высокой механической скорости бурения это не влечет ос­ложнений, поскольку вполне допустимо растепление мерзлых по­род в пределах их отрицательных температур вплоть до 0СС, так как для потери связности рыхлой породы при 0°С она еще должна воспринять скрытую теплоту плавления льда. Для оценки максимально допустимой положительной температуры промывоч­ной среды в кольцевом канале скважины при бурении в мерзлых породах в работе [23] получено выражение

1 ____ _ ^ 110

*тах 4 »

Bi VFo

наглядно показывающее влияние продолжительности циркуляции (Fo) и природы промывочной среды (Bi) на ее величину. В силу малых значений Bi, характерных для воздушной продувки, й не­больших значений Fo по причине кратковременности рейсов ко­лонкового бурения температура воздуха +5-=-Ю°С не вызывает осложнений, что подтверждается опытными данными ВИТР и практическими наблюдениями [23, 24]. В случае применения жид­кой промывочной среды (Bi->-oo) с положительной температурой растепление мерзлоты неизбежно в течение весьма ограниченного отрезка времени.

С помощью приближенных выражений типа (2.31), (2.32) или

(2.33) , (2.34) можно получить простые выражения, позволяющие с достаточной для практики точностью определять температуру нагнетаемого в бурильную колонну очистного агента, при которой ни в одной точке кольцевого канала скважины температура не бу­дет превышать /max. Это условие должно быть обеспечено техно­логическими приемами.

Комментарии запрещены.