Бурение грунтовых зондов, установка энергетических колодцев

Определение среднего квадратического отклонения данных инклииометрнческих измерений по ранее пробуренным скважи­нам позволяет рассчитать ширину доверительного интервала, п пределы которого будут попадать вновь буримые скважины с заданной доверительной вероятностью (например, 0,9; 0,95; 0,99). При малом числе скважин, участвующих в выборке (меньше 20—25), расчет доверительного интервала осуществля­ется по критерию Стыодента

/= *■ — , (11.12)

°у

гдесг — = (т/д/п — погрешность среднего арифметического, о = //± ±1оу — искомая величина, лежащая внутри доверительного ин­тервала. Критерий I определяется для значений вероятности 0,9;

0, 95; 0,99 по таблицам, которые можно найти в справочной ли­тературе по теории вероятностей.

При числе скважин в выборке более 25—30 ширина довери­тельного интервала может быть найдена по правилу «трех сигм», и соответствии с которым 99,7 % всех случайных величин данной совокупности будут попадать внутрь интервала у±3а, 95,4% — внутрь интервала у±2о, а 68,3%—внутрь интервала у±а. Зная величину доверительного интервала, можно с заданной до­верительной вероятностью определить глубину скважины, в пре­делах которой отход ее ствола от проектного профиля не пре­высит допустимую величину, найти вероятную величину откло­нения ствола скважины от заданной точки подсечения залежи полезного ископаемого, а также рассчитать количество вновь буримых скважин, траектории которых будут отклоняться от нроектных в допустимых пределах.

На рис. 11.4 приведен типовой профиль скважины с довери­тельными интервалами минимальной (±о) и максимальной (±Зо) ширины, построенный по усредненным данным статисти­ческой обработки ранее пробуренных скважин для каждого ин­
тервала глубины. На нем же нанесены интервалы допустимого отклонения минимальной (±15 м) и максимальной (±35 м) ве­личины. Из рис. 11.4 видно, что предельная глубина скважины, при которой ее отклонение от типового профиля не превысит ± 15 м, составляет 375 и 275 м для уровня вероятности соответ­ственно 0,95 и 0,99. Это означает, что для удер­жания скважины в указанном интервале отклонений ниже полу­ченных значений глу­бин потребуется приме­нить методы искусст­венного искривления.

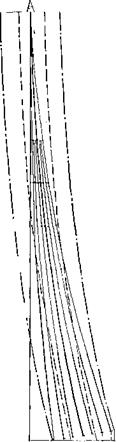
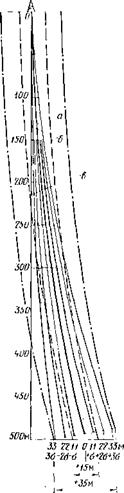Рнс. 11.4. К определению ве­роятности отклонении сква­жины от заданной траекто­рии

Для отклонения ±35 м практически вся скважина до проектной глубины 500 м не выходит за пределы этого интервала, и, следо­вательно, она может быть пройдена без применения искусствен­ного искривления.

Пределы допустимых отклонений изменяются в зависимости от стадии разведки п вида полезного ископаемого и обычно уста­навливаются в виде определенной доли расстояния I между про­
ектными точками подсечгння залежи полезного ископаемого в со­ответствии с принятой плоскостью сети скважин (0,2—0,3/). Если к отклонению скважины в плоскости геологического раз­реза и между соседними разрезами предъявляются одинаковые требования, то границы поля допусков будут представлять со­бой квадрат или окружность. Часто эти требования различны, и поле допусков приобретает прямоугольную форму, вытянутую в направлении менее жестких требований (рис. 11.5).

Если определены типовая траектория скважины и величина среднего квадратического отклонения для ее проектной глубцны, то вероятность попадания ее забоя в пределы поля допустимых отклонений оценивается как вероятность рассеивания по пло­скости случайной величины, распределение которой по этой пло­скости подчинено нормальному закону. Формула для определе­ния этой вероятности в случае прямоугольного поля допусков имеет вид

Р(Х, г, = [ф(^)-ф(^)][ф(-^)-ф(^)].

(11.13)

Для поля допусков в виде круга радиусом г

Р(Х, У) = 1—е^2о (11.14)

Если отклонение скважины возможно только в одной пло­скости, то

(11.15)

Здесь 1Х, 1У — допустимые отклонения в плоскости искривле­ния скважины н перпендикулярном к пей направлении соответ­ственно; о,., о, у — средние квадратические отклонения по осям А’ 1 г _ 1-

н У; Ф(г)——— Д с 2 с11 интеграл вероятностей, вычнеляе-

мин по таблицам в справочной литературе по теории вероят­ностей. По вычисленным значениям Р (X, У) легко определить число скважин из намеченных к бурению на данном месторож­дении, отклонения которых от типовой траектории не выйдут за пределы допустимого:

п = Р (X, У) Ы, (11.16)

где N ■— общее числе? скважин, намеченных к бурению. Следова­тельно, N — п скважин требуют применения искусственного ис­кривления для того, чтобы выдержать установленные пределы допустимых отклонений.

Комментарии запрещены.