Elastic Collapse
Elastic Collapse
|
|
The general form of elastic collapse behavior was first presented by Bresse (1859) and by Bryan (1888) (Krug, 1982). The equation for elastic collapse in thin — walled and long casing specimens is a function of rl0/1 and material constants: Young’s modulus and Poisson’s ratio.
|
|
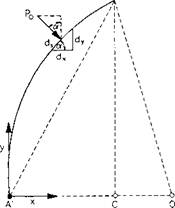
Fig. 2.9: Buckling tendency of thin-walled casing under external pressure.
Casing may be considered as an ideal, uniformly compressed ring with some slight deformation from the circular form at equilibrium. Thus, the critical value of the uniform pressure is the value which is necessary to keep the ring in equilibrium in the assumed slightly deformed shape. The ring with slightly deformed shape is presented in Fig. 2.9. The dotted line indicates the initial circular shape of the ring, whereas the full line represents the slightly deformed ring. It is also assumed that AD and GH are the axes of symmetry of the buckled ring. The longitudinal compressive force and the bending moment acting at each end of cross-section A’ — D’ are represented by ‘r, and M„ (respectively). p0 is the
uniform normal pressure per unit length of the center-line of the ring and ua is the radial displacement at A’ and D’. The bending moment is considered to be negative when it produces a decrease in the initial curvature of the circle at A.
Denoting r” as the initial radius of the ring and и as the radial deformation at B the equation of the curvature at any point on the arc A’B’ can be expressed by (Timoshenko et al., 1961):
г2 Ч — 2 (VD2 — г ■ r"
^W = _JT)W (2.ei)
where: г = г(ф) = г* — f и(ф) (2.62)
Substituting Eq. 2.62 in Eq. 2.61 and neglecting the small quantities of higher order like u2, u’u, etc., one obtains:
Similarly, the equation of the curvature at any point on the arc AB is given as:
AB{d>) = — (2.64)
Г*
The equation for the bending moment due to the deformation is given by:
-A’B’ + AB=^~ (2.65)
Ы
where:
M = bending moment due to deformation, ft-lbf.
/ = moment of inertia of the pipe, in.4
Now, substituting Eqs. 2.63 and 2.64 in Eq. 2.65, one obtains the differential equation for the deflected arc A’B1:
The vertical component of force. V0. due to pressure p0. can be expressed as:
V0 = РоШ (2.67)
= Po{r" ~ (~U0)}
= p0(r’ + u0) (2.68)
and the bending moment at B’ of the deflected ring is:
M = M0 + V0 Ж — MPc (2.69)
where:
MPo — bending moment (per unit length) due to the external pressure pQ at any section of ring.
M0 = bending moment about O.
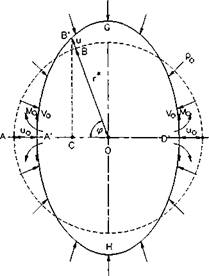
From Fig. 2.9(b), the vertical and horizontal components of force p0 are given by:
V = J p0ds cos о (2.70)
H = J p0ds sine* (2-71)
Referring to Fig. 2.9(b), the bending moment due to pressure p0. i. e., MPo, at
any point on the arc A’B’ can be expressed as:
MPo = J Po ds cosa(A’C-x) + J Po dssma(B’C-y)
= f p0(A’C — x) dx + [ p0 (B’C — y) dy J x = 0 J у = 0
= у (А’В’)2 (2.72)
Substituting Eqs. 2.67 and 2.72 in Eq. 2.69 and applying the laws of cosines one obtains:
Po
M = Mo-j(0B’ — A’O ) (2.73)
However, substituting OB’ = r" + u. and A’O = r” — ua into Eq. 2.73 and then neglecting the squares of small quantities и and u0. the bending moment becomes:
M = M0 — Po r’ {u0 — w) (2.74)
Finally, substituting Eq. 2.74 into Eq. 2.66. the final expression of the differential equation for the deflected ring becomes:
"(,) . f1 . (r’)3Po p0{r’)3uB + {r)2M0
|
‘2.75) |
‘{ф) + + — ЁГ) “<o) = Ti———-
The critical value of the uniform pressure is obtained by integrating Eq. ‘2.To. Thus, using the notation:
= 1 + Чс/1 (2’76)
one obtains the general solution:
p„ (г’)3 u0 + (?■■)2 Л/,
и(ф) = Сi cos Ф о + C2 sin Ф о +
If one now considers the boundary conditions at the cross-section A’B1 of the buckled ring, the two extreme values of о (0 and ~/2). are obtained when i/'(0) = 0 and u'(ir/2) = 0. respectively. From the first condition it follows that C2 ~ 0 and from the second, that:
C Ф sin Ф 7t/2 = 0 (2-78)
Inasmuch as Ci ф 0, it follows that sin Ф x ~/2 = 0. Thus, the equation for eigen values is:
Ф 7Г/2 = П 7Г
w’hich yields:
Ф = 2 n (n = 1.2,3…) (2.79)
For n = 1. the smallest value of Ф and. consequently, the smallest value of p0 for which the buckled ring remains at steady state, are obtained. Substituting Ф = 2 into Eq. 2.76, one obtains the general expression for critical pressure pcr:
Per = (2-80)
Г" (г.)з ‘ ;
Defining the ring as having unit width and thickness t. 1 can be written as: f3 1
/=— (2.81) 12
Substituting Eq. 2.81 into Eq. 2.80 and replacing r’ with d0J2. the equation for critical pressure becomes:
The expression for critical pressure for a buckled ring can also be used in determining the buckling strength of a long circular tube, 1 <C pipe length /. exposed to uniform external pressure. To obtain the collapse pressure (elastic range). pcr.
it is important to introduce the restrained Poisson’s number (n). The equation
of deformation according to the theory of elasticity is given by:
£* = {<rx ~ v°y) (2.88)
ev = ^ (ay — v°t) (2.84)
Provided that, the resulting radial stress is sufficiently large to compensate for the radial deformation then:
ay = v(jx (2.85)
and the axial deformation is given by:
|
|
(2.86)
where:
|
|
(2.87)
Substituting E/( 1 — i/2) for the modulus of elasticity in Eq. 2.82 and expressing diameter to thickness ratio as d0/t. the Bresse (1859) equation for calculating the collapse strength of tubular goods in the elastic range is:
|
(2.88) |
2 E 1
Pce 1 — ^ (d0/tf
where:
Pee — С ollapse resistance in elastic range (Bresse).
T)sing a value of v = 0.3, find the collapse strength of X-80. 47 lb/ft. 9| in. casing in the elastic range.
From Eq. ‘2.88:
/‘2 x (30 x 106) /0.472 3 „ .
i-m> хш) >-•"*psi