Ideally Plastic Collapse
Ideally Plastic Collapse
In the case of pipes exhibiting ideally plastic material behavior, the material at the inner surface of the pipe body begins to yield to the tangential stress induced by the external pressure at a critical value of pressure computed using the Lame formula (Grassie, 1965).
Previously, it was assumed that the wall thickness of the thin-walled cylinder was small in comparison to the mean radius and. therefore, the stress could be assumed to be uniform over the material. However, with the thick-walled cylinder (low d0/t ratio), the stress distribution is no longer uniform over the thickness of the pipe material.
If it is assumed that both the cross-section of the cylinder and the load are symmetrical with the longitudinal axis, the radial, tangential, and axial stresses are the principal stresses and, similarly, their corresponding planes are the principal planes.
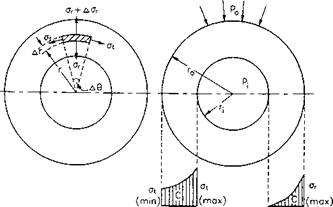
An annular ring element of radius r. subtending an angle A0 at the center of a cylinder, is presented in Fig. 2.10. <jt. at and cra represent radial, tangential, and axial stresses (respectively), acting on the ring element at any radius r. and (Fr+AFr) is the radial force at a radius (r+Ar). Thus, the radial and tangential forces can be expressed as follows:
1. Radial force:
Л FT = — aTrA9Az (2.89)
AFr+Ar = (<7r + A<Tr) (r + Аг) Ав Az (2.90)
2. Tangential force:
ft
2 AFt = 2o-(Sin — Ar Ac (2-91)
|
(2.92) |
For small angles of Ав. sin(A#/2) и Ав/2. Thus:
2 Ft = <rt Ав A г Ac
|
|
Oo Ob
|
|
|
Fig. 2.10: Stresses in thick-walled casing under external pressure. From the equilibrium conditions of the small element: |
|
(c) (d) |
|
(2.93) |
AFr+ar — AFr = <T( Ав Ar A:
Substituting Eqs. 2.89 and 2.90 into 2.93 and neglecting the product of small quantities one obtains:
|
Ar |
r AaT = (сгг — <jr) At
= at-ar
|
r dar dr |
If и is the radial displacement, the strain equations due to the principal stresses <тг, и, and <ra (all assumed positive if tensile) can be expressed as:
|
(2.96) |
и (r + Ar) — ur du 1
|
(2.97 |
2 7Г (r + u) — ‘2irr и 1
£( = = — = 77 [<7t — " (O’a + CTr)
2жг r t
|
(2.98) |
:a = 77 К — v (o> + a,) Ь
For a long cylinder, the axial strain due to the symmetrical loading condition can be considered constant and thus:
|
(2.99) |
TOC o "1-5" h z dc a ^ daa 1 daT ^ da,
dr dr dr dr
|
(2.100) |
daa _ y + dat dr dr dr
|
(2.101) |
|
0V — <7, = r |
|
dat dar |
|
Substituting Eq. 2.95 in Eq. 2.101. the following equation is obtained: |
Differentiating Eq. ‘2.97 with respect to r. equating the result with Eq. 2.96. and substituting Eq. 2.100 for daajdr gives:
However, as r(l — v) ф 0 it follows that:
at + ar = constant, which for convenience is called 2 Ad (2.103)
Substituting Eq. 2.95 into Eq. 2.103: r da,
= 2A1-2<rr (2.104)
dr
Equating to Ad and multiplying both sides by r one obtains: da,
r — l’2ff, r = 2A1r (2.105)
dr
or
— {r2ar) = 2 Kir (2.106)
dr
Finally, integrating both sides, the Lame equations are obtained for radial and tangential stresses at any radius r:
aT = K + (2.107)
and, therefore, from Eq. 2.103:
<т( = Ad — ^ (2.108)
The values of the constants Ad and I2 are determined by the terminal conditions.
If p0 is an external pressure and? and r0 are the internal and external radii of
the cylinder, respectively, then from inspection of Fig. 2.10 one obtains:
-Po = Ki+ ~ (2.109)
ro
0 = Ad + ~ (2.110)
Combining Eqs. 2.109 and 2.110 and solving for Ad and K2 yields:
|
|
|
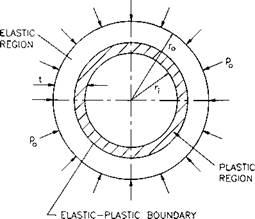
Fig. 2.11: Elastic and plastic material zones in thick-walled casing under external pressure. |
Substituting Eqs. 2.111 and 2.112 into Eq. 2.108. the tangential and radial stresses due to the external pressure p0 are respectively:
|
Po К |
|
г, 1 + i< |
|
(2.113) |
|
<rt = ~ |
|
Po к |
|
1 — |
|
(2.114) |
|
aT = — |
The maximal tangential stress. occurs at the internal surface of the pipe
|
2r |
where г = r,:
(2.115)
Thus, the critical collapse pressure. ргу1. at which the internal surface of the casing begins to yield is equal to:
2
_ 00.2 (ro, ,
РсУ1 ~ о 2 (2.116)
2 r{
where:
= tensile stress required to produce a total elongation of 0.2% in the gauge length of the test specimen.
Pcyi = critical collapse pressure for onset of internal yield in ideally plastic material (Lame).
The critical collapse pressure can be rewritten in terms of the ratio of nominal diameter, d0, to wall thickness, i. by replacing r, and r0 with [(d0/’2) — /] and (d0/’2), respectively:
|
Pcyi — 2 <7q 2 |
|
(2.117) |
(d0/t) ~ 1 (do/ty
In Eq. 2.117, the point at which the tangential stress, induced at the inner surface of the pipe body by the external pressure, reaches the yield point is considered to be a load limit. The onset of plastic deformation of the material at the inner surface of the specimen, however, does not imply that the casing has already failed rather that a plastic-elastic boundary forms (MacGregor et al.. 1948) which with increasing load, shifts from the inner surface of the cylinder toward the outer surface (Fig. 2.11). Thus, the pipe body is subdivided into an interior (plastically deformed zone) and an exterior (elastic zone).
The onset of localized yield is not the only possible indication that the critical value of external pressure has been reached. The collapse strength can also be defined as that point at which the average stress over the casing wall reaches the value of the yield limit as given by Barlow’s formula:
|
(2.118) |
|
Pcy 2 |
2 <70.2
where:
pcy2 = critical collapse pressure for onset of internal yield in casing (Barlow).
Both the Lame and Barlow formulas are used to calculate the collapse strength of the oilfield tubular goods.
ck natural yield limit is usually absent for higher steel grades; the 0.2Vc permanent strain limit is usually employed as yield strength.
|
Fig. 2.12: Buckling of long struts and the related modulus of elasticity |