TENSION
TENSION
Under axial tension, pipe body may suffer three possible deformations: elastic, elasto-plastic or plastic, as illustrated in Fig. 2.1. The straight portion of the curve OP represents elastic deformation. Within the elastic range the metallurgical properties of the steel in the pipe body suffer no permanent damage and it regains its original form if the load is withdrawn. Beyond the elastic limit (point P), the pipe body suffers a permanent deformation which often results in the loss of strength. Points Q and R on the curve are defined respectively as the yield strength (a-у) and minimal ultimate strength (au) of the material. Axial tensile load on the casing string, therefore, should not exceed the yield strength of the material during running, drilling, and production operations.
|
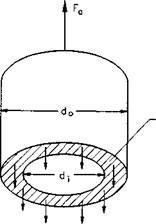
Fig. 2.2 : Free body diagram of tension and reaction forces. |
The strength of the casing string is expressed as pipe body yield strength and joint strength. Pipe body yield strength is the minimal force required to cause permanent deformation of the pipe. This force can be computed from the free body diagram shown in Fig. 2.2. Axial force. Fa. acts to pull apart the pipe of cross-sectional area of As.
Thus,
Fa — cry As (2.1)
or
F* = I °y (<%-<%)
where:
<ту = minimal yield strength, psi.
d0 — nominal outside diameter of the pipe. in.
d, — inside diameter of the pipe. in.
Calculate the pipe-body yield strength for 9| in., N-80 casing, with a nominal weight of 47 lb/ft and a nominal wall thickness of 0.472-in.
The minimum yield strength for N-80 steel:
сTy = 80,000 psi
The internal diameter, dt:
= 8.681 in.
Thus, the cross-sectional area, As, is:
= 13.57 in.2 Therefore, from Eq. 2.1:
Fa — As cTy
= 13.57 x 80,000
= 1.086 x 103 lbf
Minimal yield strength is defined as the axial force required to produce a total elongation of 0.5% of the gauge length of the specimen. For grades P-105 and P-110 the total elongation of gauge length is 0.6%.
Joint strength is the minimal tensile force required to cause the joint to fail. Formulas used to compute the joint strength are based partly on theoretical considerations and partly on empirical observation.
For API Round thread, joint strength is defined as the smaller of minimal joint fracture force and minimal joint pullout force. Calculation of these forces proceeds as follows:
Tensional force for fracture, Faj (lbf):
|
Faj = 0.95 AjpLet |
|
+ |
|
0.5 Lft + 0.14 da Let + 0.14 d, |
|
Tensional force for joint pullout: (2.4) where: Ajp — area under last perfect thread, in.2 Let = length of engaged thread, in. &up = minimum ultimate yield strength of the pipe, psi. Area Ajp is expressed as: Ajp= j[K,- 0.1425)2 — rf2] (2.5) Coupling Fracture Strength: |
|
Fa] — 0.95 AJpcruc (2.6) |
|
AJC = area under last perfect thread, in. = Ж{(1с?-(1’гоо (]/4 dco — outside diameter of the coupling, in. droot = diameter at the root of the coupling thread of the pipe in the powertight position rounded to the nearest 0.001 in. for API Round thread casing and tubing, in. cruc = minimum ultimate yield strength of the coupling, psi. EXAMPLE 2-2: For API Round thread calculate: (i) tensional force for fracture, (ii) tensional force for joint pullout. Use the same size and grade casing as in Example 2-1. Additional information from manufacturer’s specifications: Le, = 4.041 in. (long thread), au = 100,000 psi (Table 1.1). Solution: From Eq. 2.5, the cross-sectional area under the last perfect thread. AJP, is: |
|
2 |
|
Aiv = 4 [(9-625 — 0.1425)2 — 8.681 |
|
7Г |
|
= 11.434 sq. in. (i) From Eq. 2.3 one can calculate fracture force as: |
|
Faj = 0.95 x 11.434 x 105 = 1,086 x 103 lbf |
(ii) Similarly Eq. 2.4 yields the force for the joint pullout:
|
80.000 |
|
Faj = 10.8623 x 4.041 |
0.74 x (9.625) x 10
+
0. 5 (4.041)+ 0.14(9.625) 4.041 + 0.14(9.625
= 905 x 103lbf
From the above analysis the limiting factor is the joint pullout, so for API Round thread (long), N-80, 9| in. casing, the joint strength is: FaJ — 905 x 103 lbf.
Similarly, formulas used to calculate the minimal pipe-thread strength and minimal coupling thread strength for API Buttress connections can be expressed by the following equations:
Tensional force for pipe thread failure:
|
Faj = 0.95 Asp au |
|
(2.7) |
1.8 — 0.0396(1.083 — — At)dc
Tensional force for coupling thread failure:
|
(2.8) |
Faj = 0.95 Ascctu
where:
Asp = As — area of steel in pipe body, in.2 Asc — area of steel in coupling, in.2
Asc is expressed as:
|
(2.9) |
= — (d20 — d2root)
where:
dco — outside diameter of coupling, in. droot = diameter at the root of the coupling thread of the pipe in the powertight position rounded to the nearest 0.001 in. for API Buttress thread casing, in.
For N-80, 9| in. API Buttress thread connections calculate: (i) pipe thread strength, (ii) coupling (regular) thread strength, (iii) coupling ‘special clearance" thread strength. Use the data from Example 2-2 plus the additional manufacturer’s data: dco = 10.625 in. (regular), dco = 10.125 in. (special clearance). droot — 9.4517 in. Assume that erup = auc
First it is necessary to calculate the cross-sectional area of the pipe body. .4,p. and the couplings, Asc. One obtains:
Asp = j (9.625* -8.6812)
= 13.572 sq. in.
and from Eq. 2.9,
Asc = ^ (10.6252 — 8.6812)
= 18.5 sq. in. (regular)
ASP = j (10.125* — 8.6812)
= 10.35 sq. in. (special clearance)
By simple substitution of the above into the respective equations:
(i) Eq. 2.7,
Faj = 0.95 x 13.572 x (b008 — 0.0396 ^1.083 — x 9’625)
= 1,161 x 103 lbf
(ii) Eq. 2.9,
Faj = 0.95 x 18.5 x 105
= 1,757 x 103 lbf (regular)
(iii) Eq. 2.9,
Faj = 0.95 x 10.35 x 105
= 983 X 103 lbf (special clearance)
Once again it is the minimum performance characteristic of the casing which appears in the design tables. Thus, for X-80, 9| in.. API Buttress thread, the joint strengths are:
For regular couplings, Faj — 1161 x 103 lbf and for special clearance couplings. Faj = 983 x 103 lbf.
For API Extreme-line casing, joint strength is defined as the force required to cause failure of the pipe, box, or pin. The minimal value is determined by the minimal steel cross-sectional area of the box. pin. or pipe body. Formulas used to compute the tensile force for each case are:
Tensional force for pipe failure:
Fo. i = ^{dl-d]) (2.10)
Tensional force for box failure:
Fa] = ^{d)0-dl0I) (2.11)
where:
dJO — external diameter of the joint, in.
df,0I = internal diameter of the box under the last perfect thread, in.
Tensional force for pin failure:
^ = ^«„-4) (2-12)
where:
dji = internal diameter of the joint, in.
dpin — external diameter of the pin under the last perfect thread, in.
Details of the formulas used to compute joint strength are presented in API Bui. 5C2 (1987) and API Bui. 503 (1989).
Axial tension results primarily from the weight of the casing string suspended below the casing hanger or below the joint of interest. Other tensional loads can arise due to bending, drag, shock load, and pressure testing of casing string. The sum of these forces is the total tensile force on the string.