Equation 3 Shear Stress to Shear Rate Relatioship for Newtonian Fluids
The constant of proportionality, ц in this equation is known as the coefficient of viscosity or simply, the viscosity of the fluid. The viscosity of the fluid therefore determines the force required to move the upper plate relative to the lower plate. The higher the viscosity the higher the force required to move the upper plate relative to the lower plate. This simple proportionality also means that if the force, F is doubled, the plate velocity, v will also double.
The linear relation between shear stress and shear rate described above is only valid for the laminar flow of Newtonian fluids.
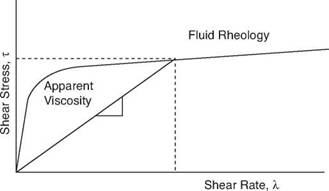
Most drilling fluids are more complex than the Newtonian fluids described above. The shear stress to shear rate relationship of these fluids is not linear and cannot therefore be characterised by a single value, such as the coefficient of viscosity. These fluids are classified as non-Newtonian fluids. As shown in Figure 7 the shear stress of a non-newtonian fluid is not directly proportional to shear rate and this is why their relationship cannot be described by a single parameter. It is possible however to define an apparent viscosity which is the shear stress to shear rate relationship measured at a given shear rate. The apparent viscosity is the slope of the line between the origin and the shear stress and shear rate intercept at any given shear rate.
|
Figure 7 Shear Stress vs. Shear Rate Relationship for non-Newtonian Fluids |
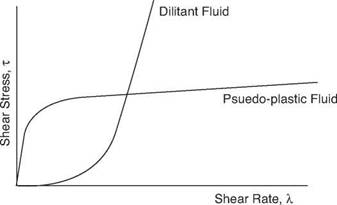
Non-Newtonian fluids which are shear-rate dependent are called pseudoplastic if the apparent viscosity decreases with increasing shear rate, and dilatant if the apparent viscosity increases with increasing shear rate (Figure 8). Drilling fluids and cement slurries are generally pseudoplastic in nature.
|
|
|
Figure 8 Shear Stress vs. Shear Rate Relationship for Psuedo-Plastic and Dilitant Fluids |
There are two standard rheological models used in Drilling Engineering. These are the Bingham Plastic and Power Law Models. The Bingham plastic and power-law rheological models are used to approximate the pseudoplastic behaviour of drilling fluids and cement slurries.
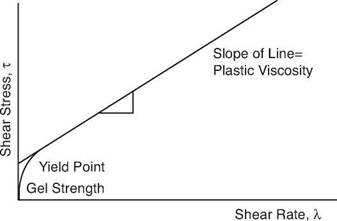
The Bingham plastic model is defined by the graphical relationship shown in Figure 9.
|
Figure 9 Shear Stress vs. Shear Rate Relationship for Bingham Plastic Fluids |
The equation of this relationship can be expressed as: t = ty + mpg