Laminar Flow in Pipes and Annuli
Laminar Flow in Pipes and Annuli
The flow regime within which the fluid is flowing in a pipe or annulus will depend on the Reynolds number for the system in question. The Reynolds number for each part of the system will however be different and it is possible for the fluid in one part of the system to be in laminar flow and the other in turbulent flow. Hence the fluid may be in laminar flow in the drillpipe but in turbulent flow in the drillcollars. The equations which describe the pressure losses when the fluid is in laminar flow can be derived theoretically. The following assumptions must however be made when developing these equations:
• The drillstring is placed concentrically in the casing or open hole
• The drillstring is not being rotated
• Sections of open hole are circular in shape and of known diameter
• The drilling fluid is incompressible
• The flow is isothermal
In reality, none of these assumptions are completely valid, and the resulting system of equations will not describe the laminar flow of drilling fluids in the well perfectly. Some research has been conducted on the effect of pipe eccentricity, pipe rotation, and temperature and pressure variations on flowing pressure gradients but the additional computational complexity required to remove the assumptions listed above is seldom justified in practice.
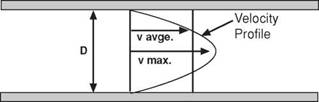
Fluid flowing in a pipe or a concentric annulus does not have a uniform velocity. If the flow pattern is laminar, the fluid velocity immediately adjacent to the pipe walls will be zero, and the fluid velocity in the region most distant from the pipe walls will be maximum. Typical flow velocity profiles for a laminar flow pattern are shown in Figure 11.
|
Figure 11 Laminar Flow Profiles in Pipes |
An analytical expression for the isothermal, laminar flow of Newtonian fluids in pipes can be derived by using force balance principles. This equation is commonly known as the Hagen-Poiseiulle equation:
|
|
|
P = |
32pvL
d2
Equation 6 Hagen-Poiseiulle equation.
Converting to field units we have the equation for the pressure loss ifor the flow of a Newtonian Fluid in a pipe
dP _ pv dL _ 1,500d2
Equation 7 Newtonian Flow in Pipes
and with some mathematical manipulation an equation for the flow of Newtonian Fluid in an annulus can be derived:
|
"N |
r
|
pv |
|
dP — = 1500 dL |
|
,2 ,2 d2_ d1 ind d1 |
|
d2+d1 |
Equation 8 Newtonian Flow in Annuli
Both of the above equations are expressed in field units.
Analytical expressions for the isothermal, laminar flow of Non-Newtonian fluids can be derived by following essentially the same steps used for Newtonian fluids. The equation for the frictional pressure loss in a pipe whilst circulating a Bingham Plastic Fluid is given by :
dP = Pnv + ,S_
dL 1,500d2 225d
Equation 9 Bingham Plastic Flow in Pipes
The equation for the frictional pressure loss in an annulus whilst circulating a Bingham Plastic Fluid is given by :
dP = Ppv + Ту
dL 1000(d2-d1)2 200(d2-d1) Equation 10 Bingham Plastic Flow in Annuli
Both of the above equations are expressed in field units.
As in the case of the Bingham Plastic Fluid the development of expressions for the pressure loss in pipes and annuli when circulating Power law Fluids is similar to that for a Newtonian fluid. The equation for the frictional pressure loss in a pipe whilst circulating a Power law Fluid is given by :
|
3+1/n 0.0416 |
dP_ kv_________
dL _ 144,000d(1+n)
v
Equation 11 Power Law Flow in Pipes
The equation for the frictional pressure loss in an annulus whilst circulating a Power law Fluid is given by :
|
n |
|
2+1/n 0.0208 |
|
kv |
|
dL 144,000d(d2-d1)(1+n) |
|
dP |
Equation 12 Power Law FIow in Annuli
Once again both of the above equations are expressed in field units.