The Equivalent Circulating Density (ECD) of a fluid
The Equivalent Circulating Density (ECD) of a fluid
It is clear from all of the preceding discussion that the pressure at the bottom of the borehole must be accurately determined if the leak off or fracture pressure of the formation is not to be exceeded. When the drilling fluid is circulating through the drillstring, the borehole pressure at the bottom of the annulus will be greater than the hydrostatic pressure of the mud. The extra pressure is due to the frictional pressure required to pump the fluid up the annulus. This frictional pressure must be added to the pressure due to the hydrostatic pressure from the colom of mud to get a true representation of the pressure acting against the formation a the bottom of the well. An equivalent circulating density (ECD) can then be calculated from the sum of the hydrostatic and frictional pressure divided by the true vertical depth of the well. The ECD for a system can be calculated from:
ECD = MW + Pd
0. 052 xD
where,
ECD= effective circulating density (ppg)
MW= mud weight (ppg)
Pd = annulus frictional pressure drop at a given circulation rate (psi) Dd = depth (ft)
The ECD of the fluid should be continuously monitored to ensure that the pressure at the formation below the shoe, due to the ECD of the fluid and system, does not exceed the leak off test pressure.
The Maximum Allowable Annular Surface Pressure — MAASP — when drilling ahead is the maximum closed in (not circulating) pressure that can be applied to the annulus (drillpipe x BOP) at surface before the formation just below the casing shoe will start to fracture (leak off). The MAASP can be determined from the following equation:
MAASP = Maximum Allowable pressure at the formation just below the shoe minus the Hydrostatic Pressure of mud at the formation just below the shoe.
Exercise 3 Leak — Off Test
A leakoff test was carried out just below a 13 3/8" casing shoe at 7000 ft. TVD using
9.0 ppg mud. The results of the tests are shown below. What is the maximum allowable mudweight for the 12 1/4" hole section?
BBLS PUMPED SURFACE PRESSURE
(psi)
|
1 |
400 |
|
1.5 |
670 |
|
2 |
880 |
|
2.5 |
1100 |
|
3 |
1350 |
|
3.5 |
1600 |
|
4 |
1800 |
|
4.5 |
1900 |
|
5 |
1920 |
Exercise 4 Equivalent Circulating Density — ECD
If the circulating pressure losses in the annulus of the above well is 300 psi when drilling at 7500ft with 9.5ppg mud, what would be the ECD of the mud at 7500ft.
Exercise 5 Maximum Allowable Annular Surface Pressure — MAASP
If a mudweight of 9.5ppg is required to drill the 12 1/4” hole section of the above well what would the MAASP be when drilling this hole section?
8.2 Calculating the Fracture Pressure of a Formation
The leak-off test pressure described above can only be determined after the formations to be considered have been penetrated. It is however necessary, in order to ensure a safe operation and to optimise the design of the well, to have an estimate of the fracture pressure of the formations to be drilled before the drilling operation has been commenced. In practice the fracture pressure of the formations are estimated from leakoff tests on nearby (offset) wells.
Many attempts have been made to predict fracture pressures. The fracture pressure of a formation drilled through a normally pressured formation can be determined from the following equations:
• vertical well and o2 = o3
FBP = 2оз — Po
vertical well and о2 > о3:
FBP = 3о3 — о2 — po
deviated well and о2 = o3
FBP = 2о3 — (Oj — o3)sin20z — po
deviated well in the direction of о2 and о2 > о3
FBP = 3о3 — о2 — (ox — O3)sin20z — po
|
where, |
|
|
FBP |
= Formation Breakdown Pressure |
|
Oi |
= Overburden Stress (psi) |
|
о2 |
= Horizontal stress (psi) |
|
о3 |
= Horizontal stress (psi) |
|
po |
= Pore Pressure (psi) |
|
0oz |
= Hole Deviation |
If the conservative assumption that the formation is already fractured is made then the equations used to calculate the fracture pressure of the formations are simplified significantly.
Eaton proposed the following equation for fracture gradients :
V
|
+GP |
Gf =[Go — Gp]
1 — V
where,
Gf = fracture gradient (psi/ft)
Go = overburden gradient (psi/ft)
Gp = pore pressure gradient (observed or predicted) (psi/ft)
v = Poisson’s ratio
Poisson’s ratio is a rock property that describes the behaviour of rock stresses (al) in one direction (least prin direction (principal stress).
|
in one direction (least principal stress) when pressure (ap) is applied in another |
Gp 1-V
Laboratory tests on unconsolidated rock have shown that generally:
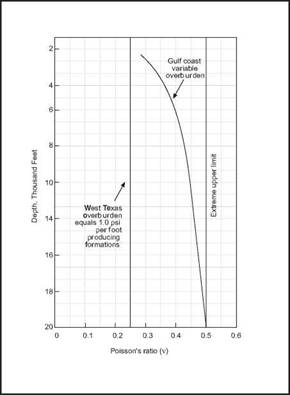
Field tests however show that n may range from 0.25 to 0.5 at which point the rock becomes plastic (stresses equal in all directions). Poisson’s ratio varies with depth and degree of compaction (Figure 27).
|
Figure 27 Variation of Poisson’s ratio with depth. Above и = 0.5 the rocks become plastic |
Matthews and Kelly proposed the following method for determination of fracture pressures in sedimentary rocks:
Gf = Gp + GK D
|
where: |
|
|
Gf |
= fracture gradient (psi/ft) |
|
Gp |
= pore pressure gradient psi/ft |
|
Ki |
= matrix stress coefficient |
|
о |
= matrix stress (psi) |
|
D |
= depth of interest (ft) |
The matrix stress (о) can be calculated as the difference between overburden pressure, S and pore pressure, P.
i. e. о = S — P
The coefficient Ki relates the actual matrix stress to the “normal” matrix stress and can be obtained from charts.
Exercise 6 Fracture Pressure Prediction — Eaton Equation
The following information has been gathered together in an attempt to predict the fracture pressure of a formation to be drilled at 8500ft:
Vertical Depth of formation = 8500 ft.
Pore Pressure = 5300 psi
Overburden pressure = 7800 psi
Poissons Ratio = 0.28 (Determined from laboratory tests on core)
a. Calculate the fracture pressure of the formation at 8500ft.
b. How would the fracture pressure of the formation at 8500ft be confirmed or otherwise when the formation has been drilled?