Turbulent Flow of Power Law Fluids in Pipes and Annuli
Turbulent Flow of Power Law Fluids in Pipes and Annuli
Dodge and Metzner have published a turbulent flow correlation for fluids that follow the power-law model. Their correlation has gained widespread acceptance in the petroleum industry. As in the case of Bingham Plastic fluids, an apparent viscosity for use in the Reynolds number criterion is obtained by comparing the laminar flow equations for Newtonian and power-law fluids. For example, combining the Newtonian and power-law equations for laminar flow yields an equation for ^ the apparent
Newtonian viscosity:
= Kd(1 — n) f3 + 1/nT 96v(1 — n) [о.0416^
Equation 25 Apparent Newtonian Viscosity for Power Law Fluid in Pipes
Substituting the apparent viscosity in the Reynolds number equation gives: _ 89,100pv (2-n) f 0.0416d ^
N
Re k I 3 +1/ n)
Equation 26 Reynolds Number for Power Law Fluid in Pipes
As in the case of the Bingham plastic model, the use of the apparent viscosity concept in the calculation of Reynolds number does not yield accurate friction factors when used with the Colebrook function. However, Dodge and Metzner developed a new empirical friction factor correlation for use with the Reynolds number given by Equation 26. The friction factor correlation is given by:
Г— 4.0, j — n/2 0.395
Vl/f = Ю55 log (Nr/ )—^2
Equation 27 Friction Factor Correlation for for Power Law Fluids
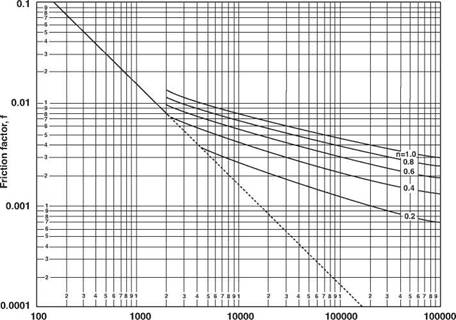
The correlation was developed only for smooth pipe. However, this is not a severe limitation for most drilling fluid applications. A graphical representation of Equation 27 is shown in Figure 14. The upper line on this graph is for n=1 and is identical to the smooth pipeline on Figure 13.
The critical Reynolds number, above which the flow pattern is turbulent, is a function of the flow-behaviour index n. It is recommended that the critical Reynolds number for a given n value be taken from Figure 14 as the starting point of the turbulent flow line for the given n value. For example, the critical Reynolds number for an n value of 0.2 is 4,200.
|
|
|
Figure 14 Friction Factors for Flow of Power Law Fluids in Circular Pipes |
The Dodge and Metzner correlation can be applied to annular flow by the development of an apparent viscosity from a comparison of the laminar annular flow equations for Newtonian and power-law fluids :
|av
|
2 + 1/n |
1,0 (d2-di) Kvn
|
0.0208 |
144,0 (Й2-Й1)1
Equation 28 Apparent Newtonian Viscosity for Power Law Fluid in Annuli
Solving for w, the apparent Newtonian viscosity gives:
|
n |
|
(1 — n) |
|
K(d2 — dt) 144v(1 — n) |
|
2 + 1/n 0.0208 |
Equation 29 Apparent Newtonian Viscosity for Power Law Fluid in Annuli
Substituting this apparent viscosity in Reynolds number equation and using Equation 23 for equivalent diameter gives:
N = 109,000pv<2 — n) ГО.0208 (d2-d1^n Re К |_ 2 + 1/n
Equation 30 Reynolds Number for Power Law Flow in Annuli