Бурение грунтовых зондов, установка энергетических колодцев

Динамическая СУВ представляет собой замкнутый контур, в ко­тором вынужденный поток водорода, проходя через ТЭ батареи и охлаждаемый конденсатор, обеспечивает удаление воды из зоны реакции.

Рассмотрим процесс тепло — и массообмена в ТЭ при испарении воды в вынужденном потоке водорода. Для исследования была при­нята упрощенная модель ТЭ (рис. 5.3). Она представляет собой два

н*

і і і m і і г і і гтттгтті і 11 і і 11

I I ( пт II I I I I п I г I I I I Г I IT IT

X/l

Рис. 5.3. Упрощенная модель ТЭ.

І

t

тонких пористых электрода с распределенными источниками тепло­ты. Толщина электродов мала по сравнению с их линейными разме­рами и не превышает 1 мм. Электроды разделены водным раство­ром гидроокиси калия. В процессе работы ТЭ в нем образуется вода и выделяется теплота. Вода образуется со стороны водород­ного электрода. Принимается, что образующаяся вода поступает в электролит и перемешивается с ним, т. е. испарение воды проис­ходит из электролита. Количество образующейся воды согласно закону Фарадея пропорционально току нагрузки. Количество выде­ляющейся теплоты определяется теплотой диссоциации при элек­трохимической реакции, омическим сопротивлением и поляризацион­ными потерями и равно

Р=1 (Еф—U),

где / — ток нагрузки; Еф — фиктивное значение ЭДС, рассчитанное по тепловому эффекту реакции; U — напряжение ТЭ.

Принимается, что выделяющаяся теплота распределяется между электродами равномерно. Поток водорода, проходя над поверхно­стью электрода, частично потребляется на реакцию, подогревает­ся и насыщается парами воды за счет ее испарения. Со стороны кислородного электрода расположен теплообменник для съема теп­лоты. Очевидно, что поле температур и концентраций электролита в реальном ТЭ должно быть описано весьма сложной системой диф­ференциальных уравнений, решение и анализ которых представляет значительные трудности.

Введем некоторые допущения, позволяющие провести количест­венные оценки и выявить основные зависимости, пе искажая суще­ства протекающих процессов.

Основные допущения и уравнения тепломассообмена

1. Рассматриваем стационарный во времени процесс.

2. Процесс токообразования протекает равномерно по всей по­верхности электрода и не зависит от температуры и концентрации электролита.

3. Коэффициенты тепло — и массообмена принимаем постоянными по длине электрода.

4. Концентрация электролита в поровом пространстве по­стоянна.

5. Теплопроводности в газе м электролите не учитываются, так как они малы по сравнению с теплопроводностью электродов.

6. Утечками теплоты с поверхности ТЭ пренебрегаем.

7. Рассматриваем одномерную в направлении потока водорода задачу, поскольку основной градиент температур и концентраций имеется в направлении потока.

8. Скорость диффузии пара с поверхности электрода в потоке водорода определяется формулой Дальтона [5.8], которая справед­лива для стационарного процесса влагопереноса при испарении жид­кости со свободной поверхности.

9. Не учитывается зависимость физических свойств электродов, электролита и хладоагента от температуры.

С учетом сделанных допущений система уравнений тепломассо­обмена для рассматриваемого случая примет следующий вид.

Уравнение теплового баланса для потока водорода

clyr (Qm, срТі = <*т®(^2 Т) + и — ,Х .

	3,36 .
і)С/>Н,07’2 —	9 1ср н/. —	(5.1)
( ^н, о, 1
‘Г V СН20,2	1 — массовый	расход

пароводородной смеси; Q“ — массовый расход сухого водорода на сходе в элемент; g*H^—удельный расход водорода, потребляемый на реакцию; CHj0= Ры2о’^нго^ — концентрация воды в потоке паро.

водородной смеси; ат — коэффициент теплоотдачи от электрода к потоку водорода; Тг — температура потока водорода; ам — коэф­фициент массо(влаго) обмена.

Уравнение теплового баланса для водородного электрода ;

ёгТ, а„ і

~ёхГ=~1ц (^0, 2“ сн2о, і) (<>Н,0 т2 + г) +

где Тг — температура водородного электрода; qH(?r — тепловыделение на водородном электроде; q^c2T — f = (£ф — U) 7-Ю4; {/ — напря­жение элемента; Еф — фиктивное значение ЭДС ТЭ, рассчитанное из теплового эффекта реакции; / — плотность тока, снимаемого с ТЭ; г — теплота испарения.

Граничные условия:

_dj І

*=о_Лс L=i’

^Н,0 ,1 ^=o = Cff, o. 1 •

Уравнение баланса масс для электролита

где Сн 0 2=у(1—Скон/100)—концентрация воды в электролите; Скон — массовая концентрация электролита; у — плотность электро­лита; DHs0—коэффициент диффузии воды в электролите.

Поскольку достоверных значений коэффициента диффузии еоды в электролите в литературе найти не удалось, принимаем, что DHao = DK0H (этим допущением несколько занижается поток воды, поскольку известно, что £>н2о > -°КОн)• Коэффициент диффузии щелочи в электролите зависит от температуры и концентрации [1.1]:

где А, В — эмпирические коэффициенты; См—молярная концен­трация; Д0 — коэффициент диффузии при бесконечном разбавлении. Используя приведенное соотношение и экспериментальные ре-

(5.6)
где #эф—эффективное термическое сопротивление теплоотдачи от кислородного электрода к хладоагенту; срха—теплоемкость хладо — агента; Те — температура потока хладоагеита. Уравнение баланса масс для потока водорода
(5.7)
гдe% = DHO — коэффициенты взаимной диффузии паров воды и водорода;
(5.8)
vh —

 

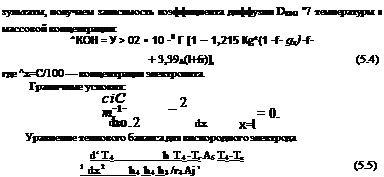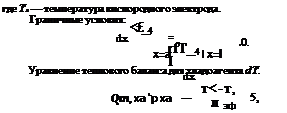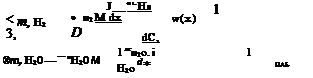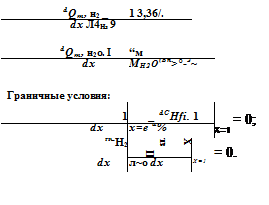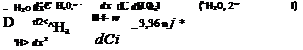Так как скорость потока w(x) — меняется ‘незначительно, то вме­сто (5.7) я (5.8) можно записать

Таким образом, получена замкнутая система дифференциальных уравненяй, описывающих процесс тепломассообмена в ТЭ. Анали­тическое решение полученной системы представляет известные труд­ности. Решение полученной системы удобнее производить числен­ным методом с применением ЭВМ. Однако для некоторых частных задач, представляющих практический интерес, можно получить ре­шения системы уравнений в явном виде.

Комментарии запрещены.