 ЭЛЕКТРИЧЕСКИЕ РАСЧЕТЫ ТОКООТВОДЯЩЕЙ ОСНОВЫ
ЭЛЕКТРИЧЕСКИЕ РАСЧЕТЫ ТОКООТВОДЯЩЕЙ ОСНОВЫ
Тенденции к уменьшению массо-габаритных характеристик, в частности толщины токоотводящей основы электродов и сечения токовых выводов, в современных электродах ТЭ при значительных развитых рабочих поверхностях могут привести к существенному снижению выходных характеристик ТЭ по сравнению с теоретическими, вызванному следующими причинами.
Падение потенциалов по модулю поверхности электродов за счет его сопротивления (а=р/6, где р — удельное сопротивление, а б — толщина токоотводящей основы электрода) приводит к тому, что точки, удаленные от токовыводящих частей, поляризуются меньше и поэтому работают при меньших плотностях тока. Вследствие этого ТЭ генерирует меньше тока, чем можно было бы ожидать исходя из измеренной разности потенциалов на внешних краях электродов.
Этот эффект существенно увеличивается, если токосъем производится не по всему внешнему краю электрода, а лишь по его части. При этом линии электрического тока искривляются (явление «стягивания») и электрическое сопротивление возрастает тем больше, чем меньше размер присоединительной части токовыводов.
Омические потери в месте присоединения токовыводящих частей к электродам (переходное омическое сопротивление) и в токовыводящих узлах на участках, где не генерируется электроэнергия, имеют также характер паразитной нагрузки.
Метод исследования работы ТЭ обычно сводится к нахождению распределения полей потенциалов и плотностей тока на электродах. Однако картины распределения этих полей могут дать только качественное представление о влиянии омических потерь на выходные характеристики ТЭ.
Бельтцером и Горовицем (США) предложена методика расчета потерь по току на одном электроде при условии одномерности поля потенциалов и вводится понятие коэффициента эффективности токосъема как отношения реально снимаемого тока на одном электроде к «идеальному», который можно было бы получить, если бы омические потери были равны нулю, при одном и том же напряжении на внешнем крае электрода.
Однако способ определения этого коэффициента, предлагаемый авторами статьи, не учитывает, что в ре — 178
альных ТЭ, во-первых, работает не один, а совместно два электрода, во-вторых, поле потенциалов неодномерно и, в-третьих, ток снимается не с внешних краев электродов, а с борнов, соединенных с токоотводящей основой электродов проводниками с некоторым омическим сопротивлением.
В связи с этим ставится задача найти количественные методы оценки омических потерь по токовыводящим частям применительно к реальным конструкциям ТЭ и провести соответствующие исследования с целью оптимизации этих конструкций.
Для количественной оценки удобно ввести интегральный пара — • метр — коэффициент эффективности токосъема ft как отношение реально снимаемого тока /р к «идеальному» /ия, который можно было бы получить, если бы омические потери были равны нулю, при одном и том же напряжении на борнах ТЭ.
«Идеальный» ток может быть определен из локальных поляризационных кривых электродов ТЭ для данных температуры, концентрации электролита и т. д.
Рассмотрим поле между двумя плоскими электродами, бесконечными в направлении оси г, ограниченными изоляторами в плоскостях х=0 и Расстояние между электродами а. Подвод и
отвод тока осуществляются по линии пересечения электродов С ПЛОСКОСТЬЮ х=0.
При нахождении поля в межэлектродном зазоре будем учитывать падение напряжения по электродам и их поляризацию. При этом допустим, что скачок потенциала (фт—ф„) на каждом из электродов линейно зависит от плотности тока. Следуя методике, предложенной Тобиасом и Вайсманом, описанную задачу будем решать с помощью функции тока ф(х, у), которая является непрерывной вместе со своими производными в рассматриваемой области [в отличие от потенциала ф(х, у)].
Уравнение Лапласа для функции тока и граничные условия имеют следующий вид:
дЦ , йгФ
дх2+ду2 =0; ‘ И-2)
![]()
![]() Ф(0, У) = 0; ф(/, у) = /
Ф(0, У) = 0; ф(/, у) = /
при 0 <1 у d
дф
М*. °) — ?п(х, о)= — ¥oi + s,
9т(х, cl) — у„(х, tf) = #62 — s2 —;
(Ц(х, 0)
~Тх = [/ — ф(х, 0)];
где фо — скачок потенциала при нулевой плотности тока; s — наклон поляризационной кривой электрода; а=р/6; р и б — удельное сопротивление и толщина материала электрода; I—полный ток в электролите.
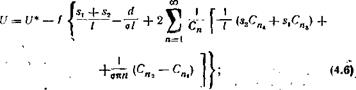 |
Найдя решение для функции тока, можно с помощью условий Коши — Римана во внутренней области ТЭ определить потенциальную функцию и разность потенциалов между любыми соответствующими точками на электродах, в том числе н на токосъемных участках электродов, что дает ВАХ ТЭ
и* = ¥oi + ?02>
где о — удельная проводимость электролита; Cn, Cni… — постоянные коэффициенты, зависящие от тангенса угла наклона поляризационной кривой, геометрических характеристик, удельного поверхностного сопротивления токоотводящей основы электродов.
Аналогичное выражение для ВАХ можно получить, решая задачу для асимметричного токосъема, когда подвод тока осуществляется, например, в точке 0, 0), а отвод в точке (I, к).
Анализируя выражение (4.6), легко показать, что при с-»-оо и а-Ю оно преобразуется в идеальную ВАХ
= ‘ (4.7)
Ток, вычисленный по (4.7), примем за идеальный, сравним его с током по (4.6) и при том же напряжении получим коэффициент эффективности токосъема, учитывающий как омические потери электрода, так и влияние сопротивления межэлектродного зазора на выходные характеристики ТЭ,
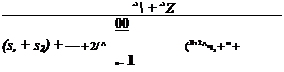
![]() (4.8)
(4.8)
+cnn(Cni — Cnt)
Из (4.8) при условии а-*-0 получим
![]() т, + s2
т, + s2
(з, — |- .9;,) — |- (I S
— коэффициент эффективности, зависящий только от сопротивления электролита. В реальных случаях сопротивление материала электродов, очевидно, не равно нулю, тогда, приняв ВАХ, учитывающую поляризацию и сопротивление слоя электролита, за идеальную, по-
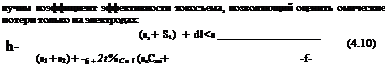 |
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
![]()
Выражения (4.15) и (4.17) позволяіот проводить приближенные расчеты эффективности токосъема на реальных электродах топливных элементов.
Понятие коэффициента эффективности, введенное для токоотводящей основы электрода, может быть распространено и на токовые выводы, хотя здесь оно приобретает несколько другой смысл.
Как уже говорилось, токовыводящие части имеют характер паразитной нагрузки и обусловливают при данном токе потери по иа-
пряжению AU. Это в свою очередь приводит к повышению напряжения на электродах, присоединенных к токовыводящим частям, меньшей их поляризации и потерям по току.
Для определения коэффициента эффективности токоотвода электродов совместно с токовыводящими частями должны быть решены совместно уравнения Пуассона (для области электродов) и Лапласа (для токовыводящих частей). В ряде случаев может быть рассчитано (или замерено) сопротивление токовыводящих частей и найден для них коэффициент эффективности (токовыводов)
(4-18)
где г ■— сопротивление токовыводящих частей, отнесенное к плотности тока на электродах,
r=AU/J; (4.19)
ДU—’падение напряжения на токовыводящих частях; / — плотность тока на электродах.
В таких случаях может быть найден общий коэффициент эффективности токосъема ТЭ
fi~fiafim — (4.20)
Как уже указывалось, коэффициент эффективности показывает ухудшение ВАХ. Если «идеальная» ВАХ U=U*—s/, то ВАХ с учетом омических потерь будет, очевидно,
U=U*—sJ/ft. (4.21)
Используя коэффициенты fig и f(m, можно построить серию ВАХ ТЭ с учетом соответствующих потерь. С другой стороны, измеряя при разных токах напряжение в некоторых характерных точках (на внешнем крае электродов, на борпах и т. д.), можно построить соответствующие ВАХ и найти экспериментально коэффициенты Эффективности fiэ И fim.
Рассмотренные выше соотношения были получены из условия одномерности электрического поля на электродах. Как правило, практический интерес представляет неодномерная задача токосъема. Ее анализ может быть осуществлен либо математическим, либо физическим моделированием.
Для решения рассматриваемой задачи может быть использован метод моделирования с помощью комбинированной модели (сплошная среда-)-./?-сетка), причем в качестве сплошной среды используются исследуемые электроды.
Для создания точной модели поля, описываемого уравнением Пуассона, требуется распределение источников тока, приложенных в каждой точке проводящей среды. Практически такое распределение источников трудно выполнимо. При моделировании распределенные источники тока дискретизируются и подсоединяются к определенным точкам, расположенным через равные промежутки, при этом каждую узловую точку электромодели присоединяют к земле через сопротивление, равное 1 /кВ, где В — поверхностная проводимость выделенного участка, которая пропорциональна площади этого участка,
k = a/s.
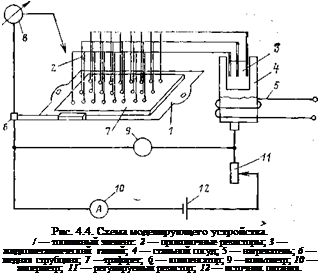 |
Для моделирования применялось устройство, схема которого представлена на рис. 4.4. В фиксированные точки рабочей поверхности электрода 1 ТЭ точечной сваркой привариваются манганиновые резисторы 2, выполненные из отрезков проволоки. Вторые концы проволочных резисторов должны находиться под каким-либо одним потенциалом относительно земли. С этой целью они погружаются в жидкометаллический галлий 3, заключенный в стальной сосуд 4, снабженный нагревателем 5. Расплавленный жидкий галлий обеспечивает хороший контакт между манганиновыми сопротивлениями и корпусом сосуда, включенного в электрическую цепь, чем н достигается равенство потенциалов.
Распределение потенциалов, получаемое при прохождении тока по электроду, снимается компенсатором постоянного тока, при этом один вывод прибора присоединяется к точке, принимаемой за нуль отсчета (например, к медной струбцине 6), а другой, на конец которого укреплена игла, поочередно присоединяется к точкам, потенциал которых мы хотим определить. Трафарет 7 служит для определения координат ввода источников тока (точки сварки электрода с манганиновыми резисторами) и точек измерения потенциалов.
В задачу моделирования входит не только нахождение распределения потенциалов на электроде, но и главным образом интегральной характеристики — коэффициента эффективности токосъема. С этой целью проводится градуировка амперметра таким образом, чтобы какое-либо, например предельное, значение его шкалы соответствовало коэффициенту эффективности токосъема, равному единице, а промежуточные значения шкалы — коэффициентам эффективности токосъема в соответствии с выражением
![]() i/I max»
i/I max»
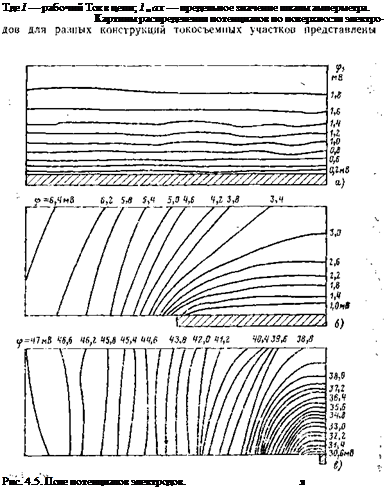 |
в —воле потенциалов при длине токосъемной шииы, равной длине электрода;* поле потенциалов при длине токосъемной шины, равной >/г длины л. электродов; в — поле потенциалов при точечном токосъеме.
J
на рис. 4.5. Неравномерность поля потенциалов сильно увеличивает — ■; ся при переходе от токосъема по всей длинной стороне токогенери — ■; рующей поверхности (рис. 4.5,а) к точечному токосъему (рис. 4.5,в).