Бурение грунтовых зондов, установка энергетических колодцев

В настоящее время расчет конденсаторов проводится обычно по среднему для всей теплообменной поверхно­сти значению коэффициента теплопередачи, которое оп­ределяется по сумме тепловых сопротивлений с обеих сторон охлаждающей поверхности. Если тепловые соп­ротивления со стороны хладоагента и стенки могут быть рассчитаны относительно легко и достаточно точно, то определение коэффициентов тепло — и массоотдачи со стороны парогазовой смеси вызывает большие затруд­нения. Критический обзор опубликованной по этому во­просу литературы приводит к заключению, что имею­щиеся опытные данные пока недостаточны для получе­ния надежных количественных зависимостей, позволяю­щих определять интенсивность процессов при конденса­ции пара из парогазовых смесей различного состава и для реальных условий работы теплообменных аппара­тов.

При конденсации пара, содержащего даже сравни­тельно небольшую примесь некондеисирующегося газа, интенсивность процесса в отличие от случая чистого па­ра определяется не столько скоростью отвода выделяю­щейся при конденсации теплоты, а главным образом скоростью переноса вещества (пара) к охлаждаемой по­верхности, на которой происходит конденсация. Поэто­му в случае конденсации пара из парогазовой смеси правильнее говорить о массоотдаче, чем о теплоотдаче, или же, когда разность температур смеси и теплообмен­ной поверхности такова, что отдачей теплоты нельзя пре­небречь, — о совместно протекающих процессах тепло — и массоотдачи. Главным источником трудностей, воз­никающих при иссследовании задачи о конденсации па­ра из парогазовой смеси является взаимное влияние процессов тепло — и массообмена.

Процесс конденсации пара из парогазовой смеси, как и всякий процесс взаимодействия между твердым телом и омывающей его средой, по физической сущности пред­ставляет собой перенос носителей энтальпии, количества движения и вещества в направлении, нормальном к по­верхности тела (такое перемещение перпендикулярно поверхности тела принято называть поперечным). Ука­занное взаимодействие выражается в том, что поверх­ность получает некоторое количество теплоты и соответ­ственно массы. При таком комплексном процессе, соединяющем в себе явления переноса теплоты и веще­ства в движущейся среде, возникают дополнительные эф­фекты, отсутствующие при раздельном их протекании. Совместные процессы оказываются вследствие этого взаимосвязанными.

Существенным для рассматриваемой задачи являет­ся еще тот факт, что твердая стенка, непроницаемая для инертного компонента парогазовой смеси, служит поверхностью стоков для конденсирующейся фазы. Вследствие наличия градиента концентраций возникает перенос массы путем диффузии в направлении, перпен­дикулярном поверхности раздела фаз. Этот диффузион­ный поток активного вещества должен сопровождаться встречной диффузией инертного компонента. Но, с дру­гой стороны, очевидно, что в силу отмеченного свойства полупроницаемости теплообменной поверхности реаль­ное существование при стационарных условиях постоян­ного видимого потока инертного компонента в направ — 1G* 243

лении нормали к поверхности является невозможным. Эти два взаимно противоположных требования удовлет­воряются благодаря тому, что возникает дополнитель­ный конвективный поток смеси, направленный навстре­чу диффузионному потоку инертного компонента и ком­пенсирующий его (эффект Стефана).

Нейтрализуя диффузионный перенос инертного газа, поток смеси увеличивает перенос пара по сравнению со случаем, когда имеют место только молекулярная и турбулентная диффузия. Система диффузионных урав­нений и граничные условия для рассматриваемого слу­чая должны, следовательно, учитывать наличие попе­речного потока активного компонента смеси, а также наличие потока Стефана.

Попытка найти строгое аналитическое решение наталкивается на непреодолимые трудности. Вместе с тем для ряда практически важных задач получено хорошее приближение. Так, С. С. Кутате — ладзе и А. И. Леонтьев [5.12] провели теоретический анализ про­цесса, в котором применили приближенные методы расчета трения, тепло — и массообмена, основанные на использовании интегральных соотношений импульсов, энергии и диффузии.

Применительно к рассматриваемому явлению тепломассоперено — са эффективными являются методы обобщенного анализа, примене­ние которых позволяет даже в наиболее сложных случаях обнару­жить и представить в явной форме связи, скрытые в уравнениях. Конкретная форма этой связи, представленная уравнениями подо­бия, устанавливается опытным путем.

Л. Д. Берман, анализируя систему дифференциальных уравне­ний процесса на базе физических представлений, предложил систему чисел подобия, позволяющую обобщить экспериментальные данные для процессов тепломассоотдачи от парогазовой смеси к поверхно­сти конденсации [5.11]:

В общем случае количественная мера результирующего эффекта одновременно протекающих процессов тепло — и ■ массообмена при конденсации пара из парогазовой смеси может быть выражена в виде условного суммарного коэффициента теплоотдачи, опреде­ляемого из равенства

Aw А

асум Q 1 ‘■ем ‘ гр

где а — коэффициент теплоотдачи; |3Р — коэффициент массоотдачи, отнесенный к градиенту парциальных давлений; г — теплота фазо­вого перехода; р — парциальное давление; R•—термическое сопро­тивление; индексы: см — смесь; ст — стенка; п — пар; гр — на грани­це раздела фаз; к — конвективное; пл—-пленка конденсата.

Так как при конденсации водяного пара теплота фазового пе­рехода значительно превышает количество теплоты, переданной кон­векцией от смеси к поверхности раздела фаз, то ак можно пренеб­речь. Кроме того, можно пренебречь также термическим сопротив­лением Ягр, так как добавление в пар инертного газа существенно понижает роль сопротивления на границе раздела фаз.

Особого внимания заслуживает оценка термического сопротивления пленки конденсата Япл. Вопрос, очевидно, не возникает, когда разделение фаз происходит с отсосом образующегося конденсата через пористую стенку. Обычно же определение перепада температуры в пленке конденсата требует проведения большого числа трудо­емких опытов при конденсации движущегося чистого па­ра. Однако, как показали визуальные наблюдения авто* ров, из парогазовой смеси с параметрами, какие обычно имеют место на выходе изТЭ, осуществляется капельная конденсация, в связи с чем парциальное давление пара у поверхности раздела фаз можно определить по темпе­ратуре стенки. Таким образом, анализ зависимости (5.30) показывает, что с точки зрения инженерной прак­тики для обобщения опытных данных по тепло — и массо — обмену при конденсации пара в присутствии неконденси — рующегося газа в теплообменных аппаратах ЭХГ до­статочно знать закономерности изменения коэффициента массоотдачи и соответственно диффузионного числ^ Нуссельта.

Получение искомой зависимости для коэффициента массоотдачи облегчается, если проводить обобщение экс­периментальных данных по рекомендации Л. Д. Бермана в относительной форме, используя в качестве масштаб­ных множителей диффузионное и тепловое числа Нус­сельта.

Тогда практически независимо от режима течения можно представить в относительной форме и при усло­вии Срп/Ср=Яп/Ят=: с учетом тройной аналогии

Nu _ Niip Nu0 Nudo ®г»

где ng=Ap/p — безразмерная разность парциальных дав­лений; Ар — разность парциальных давлений активного компонента; р — давление смеси.

В выражении (5.31) Nu и NuD — тепловое и диффу­зионное числа Нуссельта с учетом поперечного потока массы; Nu0 и NuD0 — тепловое и диффузионное числа Нуссельта для данных условий при исчезающе малом влиянии поперечного потока — масштабные множители. Масштабные множцтели отражают влияние особенно­стей гидродинамической обстановки (формы поверхности и условий ее обтекания), Nu0 и Nu^o определяются в условиях полной аналогии, что позволяет определить

их по имеющимся в литературе данным для теплообмена при отсутствии массообмена или же при малой его интенсивности, его — объемное содержание газа у стен­ки; Єгоо — объемное содержание газа в основной массе парогазовой смеси.

Соотношения Кутателадзе — Леонтьева п Бермаиа позволяют значительно сократить число необходимых опытов, решать широкий круг задач с учетом поперечно­го потока вещества, установить границы аналогии тепло­ті массообмена и при принятых допущениях хорошо со­гласуются между собой.

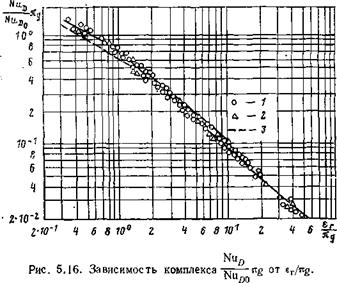
/ — данные работы 15.23]; 2 — данные работы [5.24]; 3— по уравнениям Л. Д. Бермана.

Опытные данные работы [5.14] были получены в основном па паровоздушной смеси, имеющей различ­ные параметры по давлению, температуре, концентрации воздуха при поперечном обтекании одиночного цилиндра (Re=230-:-2500), турбулентном течении внутри трубы и гравитационно-вязкостном режиме течения в гидроди­намическом начальном участке круглой горизонтальной трубы.

На рис. 5.16 в качестве примера представлена обоб­щенная зависимость, полученная при конденсации водя — ‘. 246

його пара из движущейся паровоздушной смеси при пб — перечном обтекании одиночной трубки и на вертикаль­ной плоской пластине при турбулентном движении смеси внутри прямоугольного канала. Опытные данные удовле­творительно обобщаются уравнениями, полученными на базе уравнения подобия

Nuo/NuTO = 0,7Ь7°,4 при 0,1 < sr/rcg < 1; (5.32) NuD/Nufl0= 0,7Ь70’^-0Л при а, Ле> 1. (5.33)

Кроме аналитических решений задач тепломассооб­мена и зависимостей, полученных на основании физиче­ских представлений о процессе, можно отметить эффек­тивный метод численного решения системы уравнений пограничного слоя, предложенный С. В. Патанкером и Д. Б. Сполдингом [5.13].

Метод Патанкера—-Сполдинга позволяет решать пространственные задачи совместного тепломассообмена конечно-разностным методом с использованием ломаных профилей; независимой переменной поперек слоя при этом служит безразмерная функция тока.

Перейдем теперь к рассмотрению задачи массообме­на в’конденсаторах ЭХГ.

Почти все опытные данные по конденсации пара в присутствии неконденсирующегося газа получены на паровоздушной смеси или смеси с другими тяжелыми газами, и применение рекомендованной обобщенной за­висимости для случая конденсации из пароводородной смеси без соответствующей экспериментальной проверки является некорректным, так как сведения о влияний рода газа на интенсивность рассматриваемого процесса весьма разноречивы. Реальные скорости пароводородной смеси в конденсаторах ЗХГ (Re<400) значительно отли­чаются от имевших место в опытах большинства иссле­дователей (Re>1000). Кроме того, в некоторых ЭХГ применяются малогабаритные теплообменники, процессы в которых проходят при гидродинамически и термически нестабилизированном течении смеси. В литературе прак­тически отсутствуют рекомендации по методике их рас­чета.

Такого рода теплообменные аппараты для ЭХГ иссле­дованы авторами. Конденсация осуществлялась на про­дольно обтекаемых трубках с наружным диаметром 3 и длиной 125 мм, расположенных в два ряда по 17 штук,
разделенных перегородкой и заключенных в узкий пря­моугольный кожух.

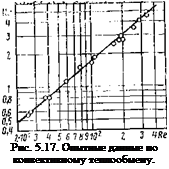При конденсации пара из парогазовых смесей с большим объемным содер­жанием газа (ег>0,85), ко­торое, как правило, имеет место в теплообменниках ЭХГ, можно считать спра­ведливой приближенную аналогию между тепло — н массообменом, и для ег/яг> >2,5 при условии jRu/Rv= = 1 справедливо соотношение Nud/Nudo^I — Для вы­явления величины Nux»o=f(Re, Ргд), определяемой по аналогии между раздельно протекающими процессами тепло — и массообмена, были проведены опыты по кон­вективному теплообмену на воздухе. Опытные данные, представленные на рис. 5.17, в диапазоне чисел Рей­нольдса Re=25-i—350 обобщены уравнением подобия

Nu0=0,048 Re°-8Pr°i33. (5.34)

По аналогии с уравнением (5.34) для диффузионного числа Нуссельта запишем

Nudo=0,048R e°’sP ід0’33. (5.35)

С целью определения возможности применения зави­симости (5.35) в расчетах конденсации паров воды из смесей с легкими и тяжелыми газами были проведены четыре серии опытов (воздух, аргон, водород и гелий). Опытные данные с разбросом ±15% удовлетворительно аппроксимируются зависимостью (рис. 5.18)

NuD= 0,048Re°’8Pr^33 (5.36)

Здесь же для сравнения представлены данные работ [5.16, 5.17], полученные при конденсации пара из влаж­ного воздуха в прямоугольных каналах в переходной области чисел Рейнольдса Re> 1000. (Можно заметить, что применение рекомендованных в этих работах расчет­ных зависимостей приводит к значительному увеличению необходимой тенлообменной поверхности.)

Авторами был испытан малогабаритный конденсатор с поперечным обтеканием шахматного пучка трубок. Трубный пучок был изготовлен из 73 трубок наружным диаметром 4 и длиной 104 мм. Опытные данные удовле­творительно обобщаются зависимостью

(5.37)

Полученная зависимость может быть рекомендована для расчета теплообменных аппаратов аналогичной кон­струкции. Порядок расчета поверхностного аппарата для конденсации пара из парогазовой смеси может быть сле­дующим.

Обычно в постановке технической задачи известны исходные данные: давление и температура влажного во­дорода на входе в аппарат, равновесная концентрация электролита, рабочий ток ТЭ, расход охлаждающей жид­кости и ее начальная температура. Априори задается конфигурация поверхности теплообмена, выбираемая в зависимости от назначения аппарата. При этом для трубчатых аппаратов задаются диаметром трубок, раз­мером сечений каналов н т. д. Определяется удельная тепловая нагрузка.

Рассчитывается коэффициент теплоотдачи со стороны хладоагента, и определяется температура поверхности конденсации.

По известным формулам для теплообмена определя­ются Nu0 и Num для данного значения числа Рей­нольдса,

По формулам (5.34), (5.36), (5.37) вычисляются зна­чения Nile.

По вычисленным значениям NuD находятся удельная тепловая нагрузка и требуемая поверхность тепломассо­обмена.

Полученные значения сравниваются с заданными.

Расчет ведется методом последовательных прибли­жений.

Комментарии запрещены.