Бурение грунтовых зондов, установка энергетических колодцев

: Водородный электрод

Активные водородные электроды обычно работают в области малых поляризаций, где фо/й^1;

b=2RT/N~60 мВ. (3.13)

При малых значениях поляризации выражение (3.4) для локальной кинетики приобретает простой вид

/л=2/оф/А (3.14)

Уравнение потенциала (3.3) записывается в виде

d2<f

dx2~U~ >

решение которого для электрода бесконечной толщины <p(*)=<Po<?_JC/i; (3.16)

У (х) =■ о<р (х) [L и У(0) = о<ро/Х (3.17)

и конечной толщины

yj = ^thS/L. (3.18)

Кислородный электрод

Ток обмена у катализаторов кислородного электро­да (Pt, Ag и др.) на 4—6 порядков ниже, чем у ката­лизаторов электроокисления водорода. Вследствие этого кислородные электроды достигают практически значи­мых плотностей тока (У>50-^100 мА/см2) при больших 100

ііоляризациях (ф0/й>5^-7). Для области больших По­ляризаций (е^’2ь ^>1; получены решения [3.9] урав­нения (3.3) при нелинейном виде локальной плотности тока (3.4), связывающие поляризацию фронтальной ср0 и тыльной <р6 сторон с толщиной электрода б

= (2W0s)l/2 {е^’ь ~ е^1)112; (3.20)

е^ь12Ьатаё[/ф-чь1Ь~ 1],/2 (3.21)

Преобразуем (3.20) и (3.21) в форму, удобную для получения зависимости активности электрода от толщины. При е*°12ь 1 из (3.6) получаем

У(0) = ^-ефо/2". (3.22)

Обозначим fjb — yJb = A<?/b, и из (3.20) и (3.22) по­лучим

JJJ (0) = (1 — е~Ач1Ь)1/2 , (3.23)

а из (3.21), используя (3.10), получим

eAip/2A arctg (^/&-l),/2 == 1,78/L,. (3.24)

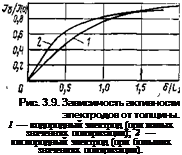
Выражения (3.23) и (3.24) могут быть легко исполь­зованы для построения графика зависимости относи­тельной активности У6//(0) от относительной толщины б/Ьэ, приведенного на рис. 3.9. Для этого, задавая опре­деленные значения Дф/й = 0,5; 1; 2 и т. д., из (3.23) и

(3.24) получим соответствующие ряды значений J& //(0) и б/Ьэ, необходимые для построения графика.

Из графиков, приведенных на рис. 3.9, следует, что при толщине активного слоя газодиффузионного элект­рода, равной эффективной толщине, активность дости­гает 0,75—0,82 активности бесконечно толстого электро­да при той же поляризации. Учитывая, что этот вывод получен при малых и больших поляризациях, есть все основания предположить, что он верен во всем интерва­ле поляризаций при условии соответствия локальной плотности тока выражению (3.4).

Комментарии запрещены.