 Гідродинаміка та теплообмін в умовах підведення газової фази в об’єм середовища
Гідродинаміка та теплообмін в умовах підведення газової фази в об’єм середовища
Газорідинні системи, основні параметри і рівняння. Природні та технологічні процеси, де відбувається взаємодія газової та рідкої фази, дуже поширені. Гідравліка газорідинних систем розглядає спільні течії рідини та газу. Такі потоки мають не тільки фіксовані зовнішні межі: стінки каналів, поверхні тіл, що омиваються, але і внутрішні межі поділу. Ці межі змінюються в часі і просторі [296]. На поверхнях розділу фаз виникають силові та теплові взаємодії, які впливають на поля швидкостей, тисків, температур, концентрацій при переході через межу поділу фаз [296]. Особливістю газорідинних систем є те, що хоча обидві фази є практично нестислими газорідинна система веде себе як стисла рідина.
Форми руху двофазних потоків набагато різноманітніші та складніші ніж форми руху та закономірності однофазних систем. Тому дослідження та узагальнення результатів в цій галузі мають більше значення ніж в гідравліці однофазних середовищ. При русі поодиноких дискретних об’єктів, наприклад, бульбашок чи краплин, можливо сформулювати задачу з необхідною точністю. Але в реальних двофазних течіях виникають проблеми, пов’язані зі змінністю меж розділу об’єктів в часі і просторі. В такому випадку вирішальне місце має фізичний експеримент і узагальнення його результатів з використанням теорії подібності. Рух середовища в будь-якій області газорідинної системи визначається рівняннями
![]() ЭТ
ЭТ
aV2T = —+ (w, gradT)
Для розрахунків газорідинних потоків використовують поняття зведеної швидкості фази. Так, якщо через переріз Q рухається газорідинне середовище з витратою газової фази V" і витратою рідкої фази V’, то зведені швидкості фаз
Wo’ = V7Q, w0" = V"/Q.
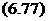 Об’ємний газовміст двофазного потоку визначається
Об’ємний газовміст двофазного потоку визначається
Р = Wo’7(wo" + wo’). (6.78)
Витратною швидкістю двофазного потоку прийнято вважати величину масової швидкості віднесену до густини рідкої фази
W0 = Wo’ + (p7p">Wo". (6.79)
Якщо двофазний потік рухається через переріз Q і газова фаза в даний момент займає переріз Q", то дійсний газовміст потоку, що є миттєвим значенням частки перерізу зайнятого газовою фазою, визначається за формулою
(6.80)
Дійсні середні та зведені швидкості пов’язані рівняннями
Середня відносна швидкість (швидкість ковзання фаз) дорівнює
лувід = w" — w’. (6.82)
Швидкість суміші визначається за рівнянням
WCM = Wo’ + Wo" = w0"/p. (6.83)
Середня дійсна густина суміші визначається
рем = р’-0 — ф) + р"-ф = р’ — (р’ — Р"Уф — (6.84)
Відносна густина суміші
ф = рем/р’ = 1 — ф-(р’ — р"Ур’- (6.85)
Основні безрозмірні параметри потоку розроблені для аналізу руху двофазних потоків на основі теорії подібності. В цих параметрах враховуються основні величини, що визначають режим руху, це
зведені швидкості фаз, їх густини та в’язкості, коефіцієнт поверхневого натягу та лінійний розмір системи.
|
Безрозмірний параметр |
Фізичний зміст |
|
< < о |
Характеризує відносний об’ємний вміст фаз в |
|
О £ О £ |
потоці |
|
wl |
Характеризує гідравлічний режим течії |
|
V |
(ламінарний, турбулентний) |
|
р: р’ |
Характеризує відношення густин та інерційних сил |
|
а |
Характеризує співвідношення сил поверхневого |
|
g-(p’-p"H2 |
натягу та сили тяжіння |
|
w2 |
Характеризує співвідношення інерційних сил |
|
g-1 |
і сил тяжіння в потоці |
За допомогою даних безрозмірних параметрів можна будувати спеціалізовані критерії, наприклад, критерій Архімеда, який характеризує співвідношення між підйомною силою і силою опору, викликаною молекулярною в’язкістю
(6.86)
Витікання газу в рідину. В процесі витікання газу через отвір в рідину розміри бульбашки збільшується до тих пір, поки не відбувається розрив шийки і відповідне зменшення поверхні розділу фаз. При малих швидкостях витікання і малій в’язкості рідини гідродинамічним опором росту бульбашки можна знехтувати, тоді баланс сил має вигляд [296]
(4/3)-7r-R30-g-(p’ — р") = 2-7r-cpo-Rr а, (6.87)
де Ro — радіус краплини в мить відриву ;
Ri — радіус отвору ;
фо — коефіцієнт звуження радіусу шийки перед початком процесу
відриву.
Тоді відривний радіус бульбашки
Експериментальні дослідження показали, що дана формула не описує у повному обсязі складність процесу витікання. При малих густинах газу швидкість його витікання може бути настільки великою, що виникають ефекти, пов’язані з стисненністю газової фази. Роботу проти сили поверхневого натягу можна виразити
dLa = 8-7r-a-RdR. (6.89)
Робота проти сили гідравлічного опору
У
де w — відносна швидкість переміщення границі поділу фаз. Після перетворень відношення робіт має вигляд
![]() dLc _ 256-a-R3
dLc _ 256-a-R3
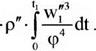 |
|
Робота утворення бульбашки відбувається за рахунок кінетичної енергії газу, що в неї втікає
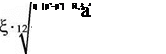 |
|
Використовуючи наведені вище залежності отримано вираз для визначення основних параметрів в процесі витікання газу в рідину
де w" — середня витратна швидкість газової фази ;
с* — коефіцієнт, що залежить від закону витікання [296].
Вільний рух бульбашок, вплив кінцевих розмірів посудини, витікання газу у в’язке середовище. Швидкість спливання бульбашки має складний характер і залежить від її діаметра. Із збільшенням діаметра бульбашки її швидкість різко зростає, далі відбувається падіння швидкості, пов’язане з різкою деформацією бульбашок і
зростанням гідравлічного опору. При цьому відбувається перехід до автомодельного до в’язкості рідини режиму.
Для такої області запропонована залежність [296]
Швидкість газової бульбашки в круглій трубі обмеженого перерізу можна записати [111]
w" = w"„-[l — (R/Ro)2], (6.95)
де w" — швидкість спливання бульбашки у великому об’ємі рідини ;
R — радіус бульбашки ;
Ro — внутрішній радіус труби.
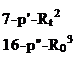 |
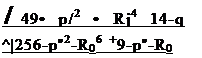 |
||
Авторами [296] на основі закону Стокса запропонована залежність для визначення середньої швидкості витікання через отвір у в’язке середовище
В’язкість рідини впливає не тільки на швидкість витікання газу через отвір, але і на величину відривного діаметра бульбашки.
Досліди підтверджують [296], що в’язкість підвищує відривний діаметр бульбашки.
Основні уявлення про гідродинаміку та тепловіддачу в об’ємі рідини за умов створення газорідинного середовища в області теплообмінної поверхні. Автором [296] запропонована залежність для швидкості підйому бульбашок в рідині
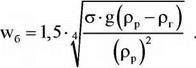 (6.97)
(6.97)
Дослідження процесів спливання поодиноких бульбашок числовими методами розглянуто в [295]. Взаємодія струменів газу з рідиною досліджувалась в [294-296]. Згідно даних [295] за умови, що критерій Рейнольдса, розрахований по швидкості бульбашки та її діаметру, більше 20, швидкість підйому ланцюжка бульбашок вище швидкості поодинокої. Причиною є певна швидкість рідини між
бульбашками. Якщо відстань між бульбашками більше діаметра каналу, то процес слід розглядати як спливання поодиноких бульбашок. Автори [294] вказують експериментально визначену межу переходу бульбашкового режиму відриву газової фази від зануреного в рідину отвору в струминний. Вона відповідає Re=200…400. В даному випадку критерій Рейнольдса розрахований по швидкості газу в отворі і діаметру отвору. Гідродинамічні особливості двофазного середовища в процесі барботування повітря в шар рідини біля вільно занурених поверхонь нагріву досліджувались в [296]. Результати переносились на пароводяні системи. Газова фаза підводилася через перфорований лист. Дійсний об’ємний газовміст залежав тільки від зведеної швидкості газової фази, що віднесена до прохідного перерізу трубного пучка. Значення складали ср=0,1.. .0,7.
В роботах [296] розглядається гідродинаміка барботажу газової фази через шар нерухомої рідини по всьому перерізу барботера. При цьому в [294] експериментальні значення складають ср=0 на стінці і ср=0,34 на осі барботера. Емпіричну залежність для визначення дійсного об’ємного газовмісту запропоновано в [296], але визначальними величинами є лише теплофізичні властивості середовища. З гідродинамічними характеристиками тісно пов’язані процеси теплообміну. В літературних джерелах [296 та ін.] наведена інформація про теплообмін за умов створення газорідинного середовища барботуванням водяної пари в об’ємі води для устаткування енергетичних об’єктів. Коефіцієнти тепловіддачі в такому випа-
о
дку складають 10… 100 кВт/(м -К). Зазначимо, що під час барботування пари через шар рідини процеси теплообміну пов’язані з ма — сообмінними процесами. Автороми [297-304] систематизовані результати значної кількості експериментальних досліджень тепловіддачі від барботажного шару до твердих поверхонь за умов масового барботажу по перерізу колонки. Загальний вигляд залежностей для визначення інтенсивності тепловіддачі
St = f(Re, Fr, Pr), (6.98)
де St =—————— число Стантона;
р w — с — At
гр р р
Авторами [294] запропонована залежність
![]()
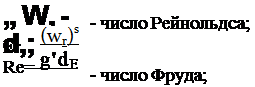 |
St = const^Re’Fr-Pr10,25.
Для хімічної промисловості досліджені характеристики теплообміну за умов встановлення теплообмінної поверхні в об’ємі рідини в барботажному та пінному режимах в контактних апаратах [296]. В процесі проведення досліджень, в більшості, для визначення коефіцієнтів тепловіддачі використовувались теплові баланси, основне рівняння теплопередачі та емпіричні залежності для теплообміну за умов вимушеного руху теплоносія. Така система визначення коефіцієнта тепловіддачі призводить до збільшення похибки визначення показника та ускладнень врахування, а тим більш, витримування на необхідних рівнях всіх параметрів, що впливають на тепловіддачу.
Для пінного режиму підведення газової фази по всьому перерізу апарату авторами [296] запропонована залежність для коефіцієнта тепловіддачі, що включає відношення густин газу та рідини
рг/рр, а також модифікацію критерію Рейнольдса Re = Wf Lv, який
vp
дорівнює критерію барботажу Кб, запропонованому авторами [296].
Авторами [276] вперше виявлена значна інтенсифікація тепловіддачі від вертикальної пластини до рідини за умов локального підведення газової фази в область теплообміну. Відзначено збільшення коефіцієнта тепловіддачі в 5 разів.
А в статті [276] інтенсифікація теплообміну за рахунок підведення газових бульбашок складає до 12 разів. А. Берглс в роботі [296] вказує на можливість підвищення тепловіддачі в кілька разів за рахунок вдування газу. Але відмічено, що підведення та відведення газової фази викликає труднощі.
Дослідження тепловіддачі в процесі омивання трубки водоповітряним потоком, що рухається в каналі, наведені в [296]. Автора
ми показано, що пікове значення ос відповідає переходу від пробкового до емульсійного режиму течії за умови дійсного об’ємного га — зовмісту 0,5…0,54.
В роботі [294] проведені попередні, обмежені дослідження впливу локального вдування повітря на тепловіддачу від горизонтальної труби до води.
Під час досліджень витрата газової фази складала (0,56…2,8) л/с. Довжина теплообмінної трубки — 0,56 м, діаметр — 8 мм. Вздовж неї було встановлено 8 отворів для підведення газу.
Виявлена інтенсифікація тепловіддачі в 1,5.. .3 рази. Показано, що вплив вільної конвекції незначний і основну роль відіграє кількість газової фази. Інтенсивність тепловіддачі описана критеріаль — ним рівнянням
Nu = 1,8-Ra°’056-Re0’3, (6.100)
де Re=w0TB’doTB/Vr — число Рейнольдса розраховане по діаметру отвору і швидкості газу, віднесеній до площі перерізу отвору.
В результаті аналізу даних літератури виявлено, що інтенсивність тепловіддачі визначається швидкістю газової фази wr, числом Прандтля Рг та питомим тепловим потоком. Емпіричні залежності розроблені для діапазонів wr=0,001…3 м/с, q=4…1200 кВт/м2, Рг=2…300.
Таким чином, в переважній більшості джерел увага приділялась процесам масового барботажу по всьому перерізу апарата. А особливості гідродинамічної ситуації та тепловіддачі за умов локального підведення газу в достатній мірі не досліджені. Відсутні емпіричні залежності для тепловіддачі за умов малих теплових потоків (q<4 кВт). А саме таких умов потребує анаеробна біоконверсія.
За різними даними наявність твердих частинок може як збільшувати, так і зменшувати інтенсивність тепловіддачі.
За даними [296] в колонних апаратах тепловіддача до трифазного середовища з С=4…10 % і wr=0,02…0,l м/с більша, ніж до двофазного і визначається за залежністю
St = 0,15 • (Rer • Frr )"°’25 • (Prc )"°’666. (6.101)
Оскільки, в літературних джерелах інформація по теплофізичних властивостях субстратів суперечна і неоднозначна, то використання залежності (6.101) для розрахунку теплообміну в реакторі БГУ вкрай складне.
В табл. 6.2 систематизовані авторами [375] залежності для розрахунку тепловіддачі від твердої стінки до середовища за умов підведення газу в область теплообмінної поверхні.
Аналіз розрахункових залежностей показує, що інтенсивність тепловіддачі визначається швидкістю газової фази, що підводиться в об’єм середовища, та його теплофізичними властивостями. Розроблені емпіричні формули використовуються в таких діапазонах параметрів: wr=0,001…3 м/с;
q=4… 1200 кВт/м2 ; Рг=2…300.