Природа тяготения и инерции. Простые квантомеханические эффекты
Природа тяготения и инерции. Простые квантомеханические эффекты
Чтобы понять природу гравитации и тяготения необходимо понять природу массы частицы (тела). В классической теории гравитации масса частицы (тела) служит мерой тяготения и инерции. Эйнштейн добавил, что масса является мерой кривизны пространства — времени. Теперь из теории УКС и ТЕЭП следует, что сферическая деформация квантованного пространства-времени является мерой массы. Таким образом, подведен базис к тому, что масса является несамостоятельным вторичным образованием в квантованном пространстве-времени, не представляя собой изолированную систему (вещь в себе), а являясь открытой квантомеханической системой, неразрывно связанной с квантованной средой как ее сгусток энергии сферической деформации среды. По сути дела, та привычная для физики классическая масса растворилась в квантованном пространстве-времени как мера вещества, которая в области микромира элементарных частиц просто не существует в реальности. Реально есть только сферически деформированная локальная область квантованного пространства-времени, энергия (56) деформации которой определяет массу частицы. Поэтому движение частицы с массой в сверхупругой квантованной среде есть волновой перенос энергии сферической деформации среды, подчинясь действию принципа корпускулярно-волнового дуализма.
Теория единого электромагнитного поля (ТЕЭП) позволяет получить уравнения описывающие массу m через вектор сферической деформации D (43) квантованного пространства-времени. Теорема Гаусса однозначно определяет массу потоком вектора ФD (44) деформации, пронизывающего замкнутую поверхность S вокруг частицы [12]
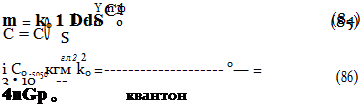 |
Выражение (85) позволяет рассматривать массу частицы (тела) как параметр сферической деформации квантованного пространства-времени. Уберите сферическую деформацию квантованной среды, и масса исчезнет. Это наблюдается при аннигиляции электрона и позитрона, когда энергия W сферической деформации частиц освобождаясь, переходит в электромагнитную энергию излучения гамма-квантов [13]
W = mC2 = koC2 <f DdS (87)
S
Выражение (87) определяет эквивалентность массы и энергии деформации квантованного пространства-времени. Сферическая деформация квантованной среды не связана с нарушением ее электромагнитного равновесия [1], поскольку квантон со всех
сторон обжимается равномерно, устанавливая одинаковое смещение зарядов со знаком (+) внутри квантона (1). Сферическую деформацию среды можно рассматривать как продольное смещение квантонов по радиусу в направление к гравитационной границе частицы (тела). Освобождение энергии (87) сферической деформации в фотонное электромагнитное излучение также связано с тем, что носителем гравитации является квантон, который одновременно является носителем электромагнетизма и переносчиком электромагнитной волны. Все эти вопросы без затруднений рассматривает теория УКС И ТЕЭП, но они выходят за рамки данной статьи.
Естественно, что причины тяготения также связаны с деформацией квантованного пространства-времени, как и причины инерции, определяя эквивалентность тяготения и инерции. Можно рассматривать причину тяготения, начиная с анализа области ультрамикромира квантонов, когда возможно изучение смещения (1) зарядов внутри квантона, как это было выполнено при анализе электромагнитных взаимодействий в квантованной среде[1]. Но можно рассматривать причины тяготения, анализируя состояние квантованной среды, как некого скалярного непрерывного поля, когда изменение топологии квантованного пространства-времени в результате его сферической деформации, ведет к градиентному перераспределению квантовой плотности среды и появлению тяготеющих сил или сил инерции.
На рис. 13 показано, что в поле тяготения Земли 1, создаваемого массой М, притягивается пробное тело 2 с массой m в соответствии с законом всемирного тяготения Ньютона с силой Fn (49), направленной к центру земли по радиусу г. Гравитационного возмущающее земное поле представлено эквипотенциалями 3 квантовой плотности среды (или гравитационного потенциала действия). Это возмущающее поле является градиентным, ослабляя квантовую плотность среды у земной поверхности, которая представлена более разряженным расположением эквипотенциалей 3. Закон всемирного тяготения Ньютона (49) базируется на решении (78) уравнения Пуассона (80) для гравитационного потенциала действия С , наличие которого в пространстве обусловлено возмущающей массой Земли М. Поэтому, для дальнейшего анализа воспользуемся формулой (67)
2 2 mM
Fn = m • gra^2 = m • grad^2 — фn ) = G —^ 1 г (88)
r2
|
2 1 3
Рис. 13. Проявление силы тяготения Fm, действующей на массу 2 (m) в градиентном вакуумном поле 3, возмущенном массой 1 (М). |
Можно анализировать градиентное распределение гравитационных потенциалов в
(88) , которое также ведет к появлению силы Fn (88). Но гравитационные потенциалы — это расчетные математические параметры гравитационного поля, а вот квантовая плотность среды — это чисто физические параметры скалярного поля, которые можно представить умозрительно, анализируя уже физическую модель тяготения. Это позволяет ставить умозрительные эксперименты, мысленно наблюдая поведение квантовой плотности среды в гравитационных взаимодействиях, избегая ошибок в анализе. Анализ гравитационных потенциалов такой возможности не представляет. Учитывая эквивалентность (66) квантовой плотности среды и гравитационных потенциалов, запишем закон (88) заменив
гравитационный потенциал действия С2 квантовой плотностью среды pi (42), которая характеризует возмущающее гравитационное поле массы М, в котором находится возмущающая масса m (рис. 13)
_ C2 „ ч _mM.
Fn = °grad(pi) = G—r lr (89)
Po r2
Выражение (89) показывает, что природа тяготения определяется градиентом квантовой плотности среды возмущающей массы М. На рис. 13 наглядно показано, как возмущающее градиентное поле массы М пронизывает пробную массу m, вызывая в ней перераспределение квантовой плотности среды, и тем самым, создавая тяготеющую силу Fn
(89) . Как видно из (89) переход на квантовую плотность среды не меняет существа закона всемирного тяготения, но придает ему физическое понимание, поскольку в (89) входит вектор деформации D (43) квантованного пространства-времени, обусловленный возмущающей массой М.
С 2 С 2
Fn = — m • grad(p1) = — mD (90)
р о ро
Из (90) следует, что причина тяготения обусловлена дополнительной деформацией D внутри пробной массы m, вызванной градиентным полем возмущающей массы М. По — видимому, именно подобное уравнению (90) пытался найти Эйнштейн, развивая теорию гравитации в ОТО, положим в основу гравитации искривление пространства-времени, используя риманову геометрию (81).
С другой стороны вектор деформации D в (90) является аналогом вектора ускорения а, устанавливая эквивалентность тяготения и инерции. Если на пробное тело массой m подействовать ускоряющей силой, эквивалентной силе Fn (90), то это приведет к градиентному перераспределению квантовой плотности среды внутри тела и появлению вектора деформации, обусловленного инерцией. Такой вектор деформации удобно
обозначить индексами Di2 , указывая на инерционные свойства деформации (индекс i) и то, что эта деформации происходит внутри тела (индекс 2)
![]() C2 i
C2 i
Fn = ma = m—° D2
Po
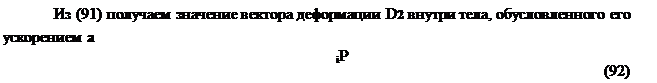
![]() C2 o
C2 o
Вынесем пробное тело 2 массой m из поля тяготения возмущающей массы М (рис. 13) и оставим воздействие силы Fn, но уже как силы ускоряющей. Как показывают проведенные
выше расчеты, в силу эквивалентности тяготения и инерции, и вектор деформации Di2 (92)
внутри пробного тела, вызванный его ускорением, должен быть эквивалентен градиенту квантовой плотности среды (90), обеспечивающий тяготение.
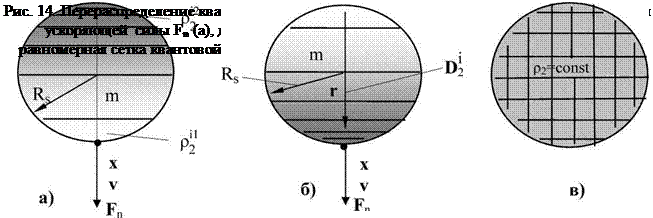
На рис. 14а показано, что воздействие возмущающей силы Fn в направлении х на пробную массу m вызывает ускорение а (92) тела, которое ведет к перераспределению квантовой плотности среды внутри гравитационной границы раздела Rs пробного тела. По сути дела наблюдаются фазовые переходы квантованного пространства-времени внутри частицы (тела) при ускорении. Видно, что внутри тела в направлении r квантовая плотность
среды увеличивается от P21 до р22, формируя внутри тела градиент квантовой плотности
среды, который определяет направление и величину вектора деформации D 2 вакуумного поля внутри гравитационной границы (рис. 14б)
 |
D 2 = grad(P 2 )
На рис. 14в показано, что отсутствие внутри пробной массы градиента квантовой плотности среды, которое представлено равномерной сеткой, указывает на то, что тело не испытывает ускорения или тяготения со стороны возмущающей массы. В этом случае пробное тело находится в состоянии абсолютного покоя или равномерного и прямолинейного движения по инерции в квантованном пространстве времени.
 |
Таким образом, новые фундаментальные открытия кванта пространства-времени (квантона) и сверхсильного электромагнитного взаимодействия (СЭВ) впервые позволяют рассматривать причины тяготения и инерции в квантовой теории гравитации. Квантон, как носитель гравитационных взаимодействий, возвращает квантовой теории гравитации классический характер, детерминистическое понимание природы гравитации и квантовой теории, которое отстаивал Эйнштейн в споре с Бором.
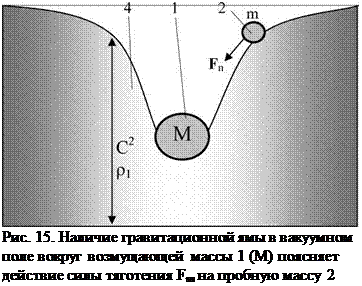
Возвращаясь к природе тяготения, необходимо обратить внимание на наличие гравитационной ямы вокруг тяготеющей массы, как это представлено на гравитационной диаграмме (рис. 11). На рис. 15 видно, как пробная масса 2, находясь внутри гравитационной потенциальной ямы, стремится «упасть» на дно гравитационной ямы под действием сил тяготения. Только на дне потенциальной ямы система принимает устойчивое состояние, связанное с действием гравитации как сил притяжения. Естественно, что на самом деле гравитационной ямы не существует при сферической деформации квантованного пространства-времени (рис. 10 и 13). Гравитационная яма появляется в результате преобразования трехмерного пространства Лобачевского в двухмерное распределение квантовой плотности среды и гравитационных потенциалов на гравитационной диаграмме. Однако сама модель гравитационной ямы очень наглядна в качестве примера действия тяготения, и никогда не рассматривалась в таком ракурсе в теории тяготения.
В общем случае, рассматривая тяготение в абсолютном пространстве-времени необходимо учитывать абсолютную скорость v на увеличение массы покоя как возмущающей М0, так и пробной массы mo. Это достигается введением нормализованного релятивистского фактора yn (70) в формулу тяготения (88)
![]()
![]()
![]()
![]() ч 2^ moМо Y пФ n) Y nG 2 1i
ч 2^ moМо Y пФ n) Y nG 2 1i
Методически проблема измерения абсолютной скорости в квантованном пространстве-времени решена, поскольку определяет квантовую плотность среды внутри частицы (тела), которая является функцией абсолютной скорости (77). Наличие такой методики в будущем позволит создать приборы, измеряющие абсолютную скорость относительно квантованной среды.
Эквивалентность тяготения и инерции, как свойств квантованного пространства — времени, позволяет рассматривать простые квантомеханические эффекты, которые хорошо известны в физике, как прямые доказательства наличия упругой квантованной среды, с которой постоянно приходится взаимодействовать в повседневной жизни:
Пример 1. Инерция. Выражение (91) убедительно показывает, что квантованное пространство-время реагирует только на ускорение, обусловленное внутренней деформацией ускоряемого тела. Любые попытки с нашей стороны ускориться или затормозиться встречают сопротивление со стороны упругой квантованной среды. Ранее физика рассматривала ускорение под действием внешней силы как свойства тела не связанные с упругой квантованной средой. Но это противоречит третьему закону Ньютона, когда любое действие встречает ответное противодействие. В данном случае действию внешней ускоряющей силы противодействует внутренняя сила, обусловленная перераспределение квантовой плотности среды внутри ускоряемого тела (90), (93), (рис. 14). Это испытывают толкатели ядра, чувствуя давление силы со стороны ядра. Любое ускорение или торможение машины, каждый ощущает на себе по перестройки квантовой плотности среду внутри своего тела, которое сопровождается силовыми толчками. Мы сами являемся частью упругой квантованной среды, которая пронизывает нас, определяя силы тяготения и инерции как градиенты квантовой плотности среды внутри тела.
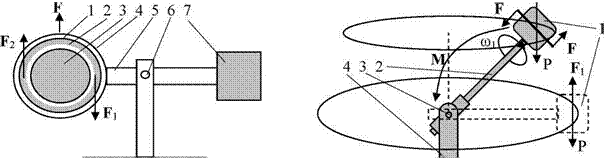
Пример 2. Уменьшение или увеличение веса гиромотора. На рис. 16a представлен стенд с гиромотором 1, установленным на рычажных весах. Гиромотор 1 содержит внешний ротор 2 в виде кольца, статор 3 и герметичный корпус 4 из которого удален воздух. Гиромотор установлен на рычаге 5 с осью 6 и противовесом 7, которые представляют собой уравновешенные рычажные весы. При пуске гиромотора наблюдается уменьшение или увеличение веса гиромотра на рычажных весах. Причем изменение веса гиромотора тем больше, чем мощнее гиромотор, то есть зависит от скорости раскручивания и момента инерции ротора 2. Для мощных гиромоторов дисбаланс сил может превосходить вес самого гиромотора.
Казалось бы, что гиромотор представляет собой закрытую систему, и момент сил, действующих на ротор, должен полностью быть уравновешен моментом сил, действующих
на статор. Никакого внешнего проявление указанных и полностью уравновешенных моментов сил не должно наблюдаться. Но это было бы так, если бы гиромотор представлял бы собой закрытую консервативную систему, действие внутренних сил и моментов которой не должно производить внешней работы по поднятию гиромотора в поле земного тяготения на рычажных весах.
Но гиромотор представляет собой открытую квантомеханическую систему, связывающую взаимодействие ротора гиромотора с упругой квантованной средой. Если заклинить ротор гироматора, то никаких внешних эффектов наблюдаться не будет, несмотря на то, что, на ротор и статор будут действовать электромагнитные силы и моменты. Но при раскрутке, ротор испытывает ускорение, которое ведет к перераспределению квантовой плотности среды внутри ротора, вызывая неуравновешенные силы взаимодействия с квантованной средой. Если ротор раскручивать против часовой стрелки, то силы сопротивления со стороны упругой квантованной среды будут направлены в сторону противоположную вращению ротора. На рис. 16а это представлено силами F1 и F2, которые действуют на ротор в локальной зоне плоскости рычага 5. Но, небсмотря на равенство сил F1 = F2, моменты которые они производят, определяются радиусами r1 и r2 от точки приложения сил до оси 6 вращения рычажных весов. Это позволяет составить баланс моментов и вычислить неуравновешенную локальную силу F
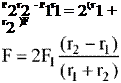 (95)
(95)
(96)
Интегрируя по всему объему ротора в проекции на горизонтальную плоскость можно определить сумму всех локальных сил F, действующих на ротор гиромотора против силы тяжести при условии раскручивания ротора, когда проявляется его ускорение. В статике, при вращении ротора с постоянной скоростью, указанные эффекты не наблюдаются, поскольку упругая квантованная среда взаимодействует с веществом ротора неравновесной силой только при его ускорении (92). Также данный эффект не будет наблюдаться на электронных весах, поскольку обусловлен действием моментов (95).
 |
б) »
Ю2
Пример 3. Обратный гироскопический эффект. Прямой гироскопический эффект определяет способность маховика (волчка) сохранять в пространстве направление оси вращения. Сегодня гироскопический эффект не имеет внятного объяснения, кроме как констатации свойств инерции вращающегося маховика, не понимая причин самой инерции. Если разбирать квантовую теорию тел вращения как открытых квантомеханических систем, то это выходит за рамки данной темы. Поэтому рассмотрим только обратный гироскопический эффект, когда принудительная прецессия ротора гиромотора приводит к появлению пары сил Кориолиса, способных создать момент, обеспечивающий подъем гироматора против сил тяготения. Это яркий пример открытой квантомеханической системы, когда работа по подъему гиромотора против сил тяготения за счет неконсервативных сил убедительно демонстрирует упругость квантованного пространства-времени. Каждый кто повторит данный опыт своими руками почувствует, что пространство-время является упругой средой, хотя сам прибор, демонстрирующий обратный гироскопический эффект не содержит пружин.
На рис. 16б представлена схема стенда, который включает гиромотор 1, закрепленный на рычаге 2. Сам рычаг 2 установлен на горизонтальной оси 3, которая связана с вертикальным валом 4. Ротор гиромотора 1 вращается с высокой частотой ю1. Вертикальный вал вращается с невысокой частотой ю2. При определенном соотношении частот вращения, когда частота ю2 соответствует частоте прецессии, гиромотор зависает на рычаге 2 в горизонтальном положении (пунктирные линии), противодействуя силе тяжести Р силой F1. Увеличение частоты ю2 ведет к увеличению силы F2, которая преодолевая силу Р заставляет гиромотор 1 на рычаге 2 подниматься вверх совершая работу. Момент М, действующий га рычаг 2 с гиромотором 1 обусловлен силами F Кориолиса, определяется длиной рычага r и моментом инерции J ротора гиромотора [39]
M = F2r = J|• ю2| (97)
Наблюдаемый эффект совершения работы по подъему гиромотора против сил тяготения — яркий пример открытой квантомеханической системы. Гиромотор не является закрытой системой консервативных сил, которые не в состоянии совершать внешней работы. Если представить, что момент М обусловлен действием консервативных сил, то никакого подъема гиромотора не наблюдалось бы, даже в том случае, если момент М в состоянии погнуть рычаг 2. Только работа внешних неконсервативных сил Кориолиса, обусловленных взаимодействием с упругой квантованной средой, в состоянии совершить работу по подъему гиромотора.
Прямой и обратный гироскопические эффекты находит различное применение в технике, и в тех случаях, когда требуется полная компенсация гироскопического момента [39-41].
Можно приводить много различных примеров простых квантомеханических систем на основе гироскопических эффектов. Но все они имеют недостаток, который заключается в том, что силы Кориолиса действующие на маховик при его переносном движении по радиусу, компенсируют друг друга, создавая момент, способный создать неуравновешенную силу только в локальной области, действующую только на ротор, но не на систему в целом. С помощью классических сил Кориолиса невозможно обеспечить подъемную силу летательного аппарата.
В тех случаях когда удается активно менять направление и величину сил Кориолиса, то возникает неуравновешенная сила системы в целом, способная поднять летательный аппарат. Подобные эффекты были обнаружены экспериментально несколько десятилетий назад английским изобретателем Джоном Серлом [42] и имеют экспериментальное подтверждение в России [43]. Но только в теории УКС и ТЕЭП на основе электромагнитной природы тяготения и инерции, впервые удалось дать теоретическое объяснение новым экспериментальным фактам, и наметить пути создания неуравновешенной силы и ее применения в летательных аппаратах [17].