Волновой перенос массы. Гравитационные волны
Как уже отмечалось, движение частицы (тела) в сверхтвердом и сверхупругом квантованном пространстве-времени возможно только в случае волнового переноса массы, которое экспериментально подтверждается принципом корпускулярно-волнового дуализма, когда частица одновременного проявляет волновые и корпускулярные свойства. То, что частица обладает волновыми свойствами положено в основу квантовой (волновой) механики. Однако расчетный аппарат квантовой механики, в силу отсутствия знаний о квантованной структуре пространства-времени и ее элементарном кванте (квантоне), был ограничен волновой функцией, имеющей статистический характер. Наличие квантованной структуру пространства-времени позволяет получить аналитический вывод волнового уравнения элементарной частицы, определяющего волновой перенос массы.
Проследим движение массы как движение гравитационной диаграммы (рис. 11) когда сферически симметричное распределение квантовой плотности среды, определяющее массу элементарной частицей переносится в квантованной среде со скоростью v. Запишем функцию распределения квантовой плотности среды р1 (77)
р1 р о
 |
 |
 |
Рассмотрим простейший случай, когда частица движется в квантованной среде по инерции, а изменение квантовой плотности среды проследим на движении сферы с радиусом г
Перенос гравитационной диаграммы по оси Х на расстояние дх ведет к изменению квантовой плотности среды на величину др при скорости движения электрона v по оси Х
дх v = — dt
Из (136) находим частную производную по оси Х при у=0, z=0 и г=х
др Rs
= р о-Т Y n (139)
dx х2
Заменяем в (139) приращение дх эквивалентным приращением v3t=3х из (138) и определяем частную производную от (136) по времени t
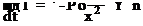дР =„ р RS
Подставляя в (140) значение частной производной по оси Х из (139) получаем волновое уравнение электрона при его движении в квантованной среде по оси Х
v dt
 |
 |
 |
 |
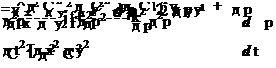Движение электрона по оси Х одномерное. Однако движение электрона охватывает некий объем пространства, производя волновые процессы также по осям Y и Z. Учитывая сферическую симметрию электрона скорость распространения волнового переноса квантованной среды по осям Y и Z, отвечающая за формирование гравитационной ямы электрона, также равна скорости движения электрона v. Это позволяет записать трехмерное волновое уравнение электрона в частных производных по ортам i, j, k
Для одиночной волны, движущегося равномерно и прямолинейно частицы без излучения, и обеспечивающей перенос массы электрона по инерции, решение уравнений (142).. .(145) определяет сферически симметричное распределение квантовой плотности среды (р1 и р2) (77) и гравитационных потенциалов (ф1 и ф2) (78)
Движение частицы, описываемое волновыми уравнениями, указывает, что внутри квантованной среды происходят сложные волновые процессы, связанные с
перераспределением квантовой плотности среды в пространстве. Волновые уравнения легко преобразуются в уравнения движения (138).
Необходимо отметить, что в отличие от волновых уравнений электромагнитного поля [1], волновые уравнения частицы (тела) имеют продольный характер деформации квантованной среды, а не поперечное смещение зарядов в квантонах в электромагнитной волне. С волновым переносом массы, как типичным примером гравитационной волны с продольным характером деформации квантованной среды, мы регулярно сталкиваемся в повседневной жизни. По этой причине многолетние попытки обнаружить гравитационные волны с поперечным характером колебаний до сих пор не увенчались успехом [45], и, по — видимому, не увенчаются.
 |
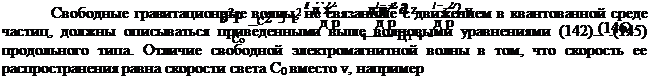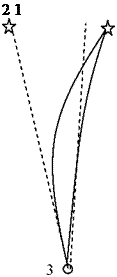
Рис. 18. К эффекту Козырева по раздвоению звездного источника света и гравитационной волны в результате различного искривления луча света и луча гравитационной волны.
1 — истинное положение звезды;
2 — кажущиеся положение звезды в результате искривления луча гравитационной волны;
3 — наблюдатель.
Волновое уравнение (146) свободной гравитационной волны в упругой квантованной среде подобно уравнению ультразвуковой волны, которое также является уравнением продольного типа. Волна распространяется в виде зон продольного сжатия и разряжения квантованной среды. По-видимому, одним из первых открыл подобные волны профессор Вейник [12]. Возможно, открытие Вейника пересекается с волнами Козырева [46]. В теории УКС и ТЕЭП показано, что топология электромагнитной и гравитационной волны, совершенно различные. Топология космического квантованного пространства-времени связана с его искривлением. Это дает основания полагать, что в искривленном пространстве — времени луч света и луч гравитационной волны идут по различным кривым траекториям, создавая эффект Козырева по раздвоению единого звездного источника излучения [46]. На рис. 18 показано возможное искривление лучей света и гравитационной волны, которые позволяют наблюдателю 3 одну и туже звезду 1 регистрировать в разных координатах (1 и 2) звездного неба. Исследования теории продольных гравитационных волн в упругой квантованной среде позволили предложить новые способы их излучения и приема [15], которые могут найти различное применение в различных областях: от техники связи до медицины. Учитывая возможную колоссальную проникающую способность гравитационных волн можно рассчитывать на создание принципиально новых систем диагностики, возможно более безопасных, чем рентгеновское излучение. Но все это требует всестороннего и грамотного исследования.