Бурение грунтовых зондов, установка энергетических колодцев

Увеличение темпа и объемов буровых работ, а также повышение их качества и эффективности возможно при автоматизации всех информационных процессов, связанных с управлением процес­сом бурения. При этом автоматизация должна охватывать не только сбор и первичную обработку измерительной информации, регу­лирование отдельных параметров, а, главным образом, анализ полученной информации, диагностирование состояния буровой установки, принятие оптимальных решений по управлению про­цессом строительства скважины. Для решения этих проблем тре­буется построить обобщенную модель структуры и законов функ­ционирования бурящейся скважины, характеризующих поведение объекта количественно, структурно и логически [9].

На уровне количественных свойств и отношений для бурящей­ся скважины можно указать конечное множество переменных, практически полно описывающих ее функционирование — харак­теристический вектор. Определение компонент этого вектора яв­ляется сложной задачей, решаемой технологами совместно с дру­гими специалистами на основании изучения природы и особен­ностей протекающих на бурящейся скважине процессов.

Пусть

и={^, и2,..„ Ц,…, и„} (1.1)

множество технологических параметров, описывающих процесс строительства скважины.

На первом этапе автоматизации информационных процессов при бурении скважины необходимо решить задачу автоматизи­рованного сбора информации о параметрах множества U. В за­висимости от целей и способа бурения это множество может быть соответствующим образом деформировано. Из всех способов бу­рения наибольшее распространение в России получило турбин­ное бурение. В настоящее время ряд важных параметров турбин­ного способа бурения не может быть измерен (скорость враще — * ния долота, вращающий момент на валу турбобура); кроме того, некоторые параметры измеряются косвенно, с большими мето­дическими погрешностями (нагрузка на долото, скорость меха­нического бурения). О ряде параметров имеет смысл говорить лишь когда буровая скважина находится в определенном классе состояния. В общем случае каждому параметру или множеству параметров можно поставить в соответствие предикат, опреде­ляющий его наличие или отсутствие в характеристическом век­торе [8]:

P(UX, U2, …, U-„ ОД 1.0. (1.2)

Задача автоматического определения границ и областей су­ществования технологических параметров была частично реше­на и описана в работах [101, 121, 141, 168].

Между элементами U/eUимеются определенные количественные отношения. В зависимости от конкретно решаемой задачи данные отношения могут иметь вид дифференциальных уравнений [64], эм­пирических формул [122, 121, 141], вероятностных моделей [101].

В настоящее время для описания процесса бурения используются детерминированные и вероятностные модели. Наиболее полно де­терминированный подход к выявлению математических моделей про­цесса бурения выражен в классических работах русских и американ­ских исследователей: В. С. Федорова, Н. И. Шацова, В. В. Симоно­ва, М. Г. Бингхема, П. В. Балицкого. J1. А. Шрайнера, В. С. Маурера, М. М. Александрова, Ю. Р. Иоаннесяна, Р. М. Эйгелеса, А. X. Мир- заджанзаде, J1. Е. Симонянца и др.

На рис. 1.1 показана информационная структура модели про­цесса бурения, наиболее полно отражающая взаимосвязи, воз­никающие при реализации процесса.

Обобщенная модель процесса бурения определяется моде­лями условий разрушения (1.1) и заданных свойств промы — йочной жидкости (ПЖ) на входе в скважину (1.2), зависящи­ми от режимно-технологических параметров и свойств ПЖ

моделями факторов, ограничивающих процесс бурения — конструкции скважины (2.1), типа долота и забойного двига­теля (2.2), компоновки низа бурильной колонны (КНБК) при наклонно-направленном бурении (2.3), зависящими от огра­ничений, накладываемых на режим бурения; моделями гор­ной породы — фильтрационно-емкостных свойств (3.1), ха­рактера насыщения (3.2), прочностных свойств в забойных условиях (3.3), физико-химических свойств (3.4), определяе­мыми физико-механическими и физико-химическими свой­ствами горной породы.

На выходе обобщенной модели процесса бурения появляются параметры процесса (4), являющиеся следствием реализации про­цесса и изменения свойств горных пород (мгновенная скорость Кмгн, дифференциальный расход Д(), амплитуда А и частота виб­раций/ верха бурильной колонны), изменения свойств ПЖ про­тив модели заданных свойств ПЖ (плотности — Др, кинематиче­ской вязкости Ду, газосодержания — АГПЖ, pH— АрН, окислитель — но-восстановительного потенциала — Де//, ионного состава — АсХ и т. п.), а также приращение момента на роторе — ДМр, мощно­сти привода насосов — Д#„ и т. д.

С некоторой задержкой, обусловленной временем отбора и анализа, на выходе обобщенной модели бурения появляется ин­формация о свойствах горных пород, определенных по шламу (керну) в зависимости от вида бурения (5).

Итоговой информацией (б) являются модели технологических показателей (6.1), экономических показателей (6.2) и показате­лей качества построенной скважины (6.3), определяемые основ­ными (скорость проходки — Ум, проходка на долото Ню время бурения — Гд, стоимость метра проходки — С„), дополнительны­ми (время СПО — Тто, время ремонта — Грсм, износ долота — И, соответствие параметров кривизны заданным — а, (3, М) и ито­говыми (коммерческая скорость бурения IV) технико-экономи­ческими показателями.

Ограничения, не зависящие от режима бурения (2), сказыва­ются как на режимно-технологических параметрах и свойствах ПЖ (2—1), так и на выходных технико-экономических показа­телях процесса (2—6).

Параметры процесса (4) и результаты определения свойств горных пород по каменному материалу (5) являются элементами модели горной породы (3.1—3.4), поэтому они находят свое от­ражение как в параметрах свойств процесса (3.1—4.1, 3.2—4.2, 3.3—4.3, 3.4— 4.4), так и в результатах непосредственного опре­

деления свойств пород (3.1—5.1, 3.2—5.2, 3.3—5.3, 3.4—5.4).

Это дает возможность реализовать обратные связи (4—3) и (5—3) с моделями физико-механических свойств горных пород, а через их соответствие действительным влиять на выбор ре­жимно-технологических параметров и свойств ПЖ (связи 3—4, 4— 1), а также на конечный результат — качество и полноту гео­логической информации (связи 3—5, 5—6).

Определенным образом на параметры процесса и информа­тивность по каменному материалу влияют и ограничения, не за­висящие от режима бурения (связи 2—4, 2—5).

Параметры процесса (4), такие как Утн, Л0, Ар, Ау, находятся в зависимости от режимно-технологических параметров (связи 1—4), так же как полнота получения информации по каменному материа­лу зависит от технико-экономических показателей (повышение ско­рости бурения и скорости подъема грунтоноски приводят к умень­шению выноса керна, несоблюдение режима промывки перед подъ­емом инструмента — к потере шлама и т. п. — связи 6—5).

Таким образом, предложенная информационная структура модели процесса бурения (см. рис. 1.1) показывает всю слож­ность и взаимообусловленность обобщенной модели процесса бурения, но в то же время открывает реальные пути учета ме­шающих факторов как для получения информации о свойствах горных пород, так и для управления процессом разрушения гор­ных пород на основе информации об их свойствах.

Многомерность обобщенной модели процесса бурения, являю­щейся сочетанием технологического процесса, свойств горных по­род и целого ряда ограничений, вносимых в процесс, будет более подробно рассмотрена в следующих разделах. Сейчас же рассмотрим наиболее простые модели процесса бурения.

а также среднее значение механической скорости, определяемое на некоторый интервал времени, например за одно долбление,

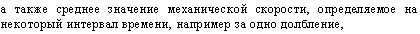Механическая скорость бурения характеризует темп продви­жения забоя скважины при разрушении горных пород. Различа­ют мгновенную механическую скорость

где Я— проходка за время Т.

Изучению характера изменения механической скорости буре­ния в процессе работы долота на забое посвящено множество исследований [8, 20, 101, 102, 121, 168], и большинство авторов приводит эмпирическую зависимость вида:

V = AnaGЯ, 0-3)

где А — коэффициент пропорциональности (коэффици­ент буримости); п — частота вращения долота;

G — нагрузка на долото;

а, Я — постоянные для данного типа породы коэффи­циенты.

Механическая скорость бурения для долот с фрезерованным вооружением от начала к концу рейса изменяется по закону ес­тественного износа [20] долота, определяемого формулой

V«=Vo е“*’=Т“ТГ-е“*’’ <М>

1 + b

где V„ — начальная механическая скорость бурения;

а, b — параметрические коэффициенты, характеризую­щие сочетание «долото-порода»; о — время;

К — показатель часовой скорости износа долота.

В методике, разработанной институтом ВНИИБТ [97], при­ведены следующие модели: Т = Т0 — aG — bn,

V(t) = KGan»( + a, t + a2t2), (1.5)

где V(r) — мгновенная скорость бурения, м/ч;

G — осевая нагрузка на долото, тс;

п — частота вращения долота, мин^1;

1 — текущее время, ч;

Т — стойкость долота по опоре, ч;

К, а, Я, Т0, а, Ь, аи а2 — коэффициенты выбранных

моделей.

Уравнение (1.5) можно представить в виде:

т = К(1 + а^ + а^),

где К-, = КС"п1’’ — стационарная часть, зависящая от режим­ных параметров, свойств породы, типов долот и других факторов. Полином 2-й сте­пени по Г описывает износ вооружения до­лота во времени, коэффициенты ах и а2 в общем случае являются функциями ре­жимов, и их можно аппроксимировать многочленами вида:

я,(<7, п) = ф0 + ф, С + ф2/г + ф|2С//;

д2(С, п) = + г|>2п + г|)|2С«.

Применение полиномиальной модели для описания износа воо­ружения долота вместо с к’ вызвано тем, что полиномиальная мо­дель позволяет применить упрощенную процедуру определения ко­эффициентов при обеспечении необходимой адекватности модели.

Многообразие моделей, приведенных в работах [48, 102], сви­детельствует, во-первых, о том, что исходным для них является уравнение вида (1.3) и, во-вторых, подчеркивает всю сложность моделирования процесса бурения. Поэтому в практике бурения рациональные режимы процесса определяются только по двум основным технологическим параметрам — нагрузке на долото С и скорости его вращения п.

Для более детального представления процесса бурения модели видов (1.3) — (1.5) обычно дополняются зависимостями [17]:

TOC o "1-5" h z Т — 6

в (7с,|и/?| ’ (1-6)

т с

0 С4г/2 ’ (1-7)

где Ть, Т0 — соответственно сроки службы шарошечного долота по вооружению в опоре; в — постоянная, зависящая от типа и конструк­ции вооружения долота;

С — постоянная, зависящая от конструкции опо­ры, качества контактных тел и ее смазки;

а,, а2, рь (32 — коэффициенты, зависящие от абразивности промывочной жидкости и скорости враще­ния долота.

На основе анализа зависимостей механической скорости бурения от параметров процесса бурения и конструкции скважины в работе [81] выведено обобщенное уравнение скорости бурения:

/

е

10 &Рр J

0_ 2 ё

а

0р_ 5нц.

уы=к,

(1-8)

—

где К, С £ п О р д й п А/’р а, Ь

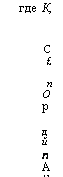коэффициент буримости, характеризующий петро — физическую характеристику горной породы (учиты­вает прочностные и фильтрационные свойства);

— нагрузка на долото;

— площадь зубьев долота, находящихся в контак­те с породой;

— частота вращения долота;

— расход промывочной жидкости;

— плотность промывочной жидкости;

— площадь сечения промывочных отверстий насадок;

— вязкость промывочной жидкости;

— диаметр бурильных труб;

— диаметр скважины (долота);

— расчетное дифференциальное давление;

, с, е,/— коэффициенты модели (1.8).

Использование формулы (1.4) принципиально возможно толь­ко в случае разбуривания пород с неизменными петрофизиче — скими характеристиками при постоянных режимно-технологи­ческих условиях, что на практике встречается весьма редко. На­пример, Уа может принимать самые различные значения в зави­симости от того, в каких породах начат рейс долота.

Зачастую рейс долота начинается со скоростью У0, меньшей скорости бурения в середине рейса, тогда уравнения типа (1.4) вообще теряют смысл. Например, данные по Западной Сибири показывают, что функция У=/0) в большинстве случаев не под­чиняется уравнениям вида (1.4).

Рассмотрим изменение скорости бурения во времени с других позиций. В обобщенном уравнении (1.8) некоторые параметры в течение рейса не изменяются, другие же меняют свои значения по тем или иным причинам.

Например, такие параметры, как £) и с/, 5Н и (2, р и р., а также и ДРр, как функция Н, р и (), как правило, остаются в рейсе постоянными. В роторном бурении постоянной величиной в рейсе является частота вращения долота п. Величина (С/£к) не может быть постоянной даже при неизменном значении (7, так как по мере износа долота увеличивается. Переменной величиной яв­ляется и коэффициент буримости, он может иметь постоянные значения лишь для небольших (по глубине) участков разреза. В турбинном бурении переменной величиной является и п, ме­няющая свои значения с изменением С.

Таким образом, для одного рейса долота постоянными вели­чинами являются:

для роторного бурения

Qp_ Ли.

(1.9)

D У( 10

2d

для турбинного бурения

(1.10)

0Р. ТГАТ

S„nJ y2d)

где К тр = const (для данного рейса) — постоянный коэффи­циент технологичности процесса для роторного бурения;

Кх тт = const (для данного рейса) — постоянный коэффициент технологичности для турбинного бурения.

Переменными технологическими величинами для рейса являются: для роторного бурения

для турбинного бурения

к

2 пт

пь,

V^K У

(1.12)

где К2тр — переменный коэффициент технологичности процесса для роторного бурения;

К2тг — переменный коэффициент технологичности процесса для турбинного бурения.

Итак, переменными технологическими величинами для рей­са являются:

— для роторного бурения — С и при С = const — только

— для турбинного бурения — G, SK и п, а при С = const, П = const — ТОЛЬКО SK.

Таким образом, при поддержании постоянных режимных параметров единственной технологической причиной (при КЪ = const) падения скорости бурения в рейсе долота является увеличение контактной площади зубьев долота в процессе изно­са (от 5Kmin до SKtm%) и, как следствие этого, уменьшение удель-

ного давления на породу (/yil

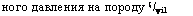
V^k J

Известно [71], что для эф-

фективного объемного разрушения породы при бурении шаро­шечными долотами должно соблюдаться условие

С = а Рш 5К, (1.13)

где а — коэффициент, учитывающий влияние факторов, действующих в реальных условиях (так как эти факторы учитываются другими коэффициента­ми, принимаем а= 1);

Рш — твердость породы при вдавливании штампа. Можно сказать, что при (7/5к > Рш разрушение породы будет объемным, при (7/5^ < Рш — уста­лостным, а при Сг/Ук < Рт — будет наблюдаться процесс истирания.

Площадь 5ктй1 опускаемого в скважину долота известна [148] или может быть подсчитана [71]; динамика изменения во вре­
мени и определяет динамику изменения Уы во времени (при по­стоянных параметрах, входящих в уравнение (1.8).

Таким образом, задача об определении механической скоро­сти бурения V(t) сводится к определению SK(t). Эта задача реше­на в работе [58]. Теперь обобщающее уравнение скорости буре­ния можно переписать в следующем виде:

f

D_ 2 d)

10 АЛ

р

а

Q р SH1

(1.14)

sK(t)

С учетом формул (1.9) — (1.12) имеем: для роторного бурения

Vjr) = К, К, .фЛГ: .,„(/), (1.15)

для турбинного бурения

К(0 — к,>к1тгк2тг(о. (1.16)

КЛО _____________ 60_ К г ■ к 2, (0 т. к^-кглУ

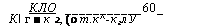Для условий электробурения можно применить формулу (1.15). ‘ Коэффициент буримости, содержащий информацию как о прочности, так и о фильтрационных свойствах горных пород, может быть определен по формуле:

V. v и т. к — к’ (л ’

(1.17)

где Т — продолжительность бурения /-го погонного метра скважины.

При анализе буровой как объекта управления в АСУТП-БУ- РЕНИЕ выделяются два основных контура управления: I) буро­вая—оператор—буровая; 2) буровая—УБР—буровая (иногда — че­рез РИТС). Оба контура управления объединены одной общей целью: выполнение планового задания (достижение проектной глубины скважины при соблюдении определенных значений гео­логических, технологических и технико-экономических показа­телей). Тем не менее задачи, решаемые в них, различны.

Задачи, решаемые в 1-м контуре управления, являются опе­ративными, и эффективность их решения зависит от таких фак­торов, как правильно составленный геолого-технологический наряд, полнота и достоверность оперативной информации о про­цессе, поступающей к бурильщику, профессиональные качества бурильщика. В связи с дискретностью характера процесса буре­ния основная задача — достижение проектной глубины скважи­ны — может быть разбита на ряд подзадач, общим для которых является минимизация времени или затрат на проведение ряда последовательных операций в рамках различных технологиче­ских ограничений. К наиболее важным операциям относятся: механическое бурение, промывка, спуско-подъемные операции (СПО), простои, геофизические работы.

При выполнении операции «Механическое бурение» решают—4, ся следующие задачи: ведение оптимального режима бурения, пре­дупреждение аварийных ситуаций, своевременное оповещение РИТС о нарушении технологии ведения работ, вызванных не­предвиденными обстоятельствами. Задачи, решаемые при прове­дении остальных операций, сводятся к контролю режимных пара­метров с целью предотвращения, ликвидации аварийных ситуа­ций (гидроразрыв пласта, нефтегазопроявление и выброс), к кон­тролю и регулированию режимных параметров бурового оборудо­вания, ведению правильной организации труда, снабжению буро­вой необходимыми материалами.

В функции 2-го контура управления входят составление геолого­технологических нарядов (ГТН) на бурение скважин, распределение людских и материальных ресурсов, оперативный контроль, прогнози­рование и корректировка выполнения планов работ по бурению.

Эффективность управления производственными процессами за­висит, главным образом, от полноты, достоверности, своевремен­ности доставки информации на соответствующие уровни управле­ния, алгоритмов обработки, формы представления.

Выбор рациональных режимов бурения с целью повышения эффективности проводки скважин необходимо производить с позиций системного подхода [101], так как выбранный, согласно ГТН, рациональный режим бурения может не соответствовать требуемому в настоящий момент, а, следовательно, должен кор­ректироваться в процессе бурения, для чего необходимо изме­нять управляющие воздействия (нагрузку на долото, обороты долота, расход промывочной жидкости) с целью обеспечения це­ленаправленного приспособления их к изменяющимся забойным условиям (возмущающим воздействиям).

В свою очередь для этого на буровой необход има автоматиче­ская информационно-измерительная система для сбора, первич­ной обработки, хранения и передачи статистической информа­ции о параметрах процесса бурения, а также для принятия цело­го ряда оперативных решений на основе алгоритмов, реализуе­мых непосредственно на буровой. Введение в теорию и практику бурения вероятностных моделей, методов исследования опера­ций, прогнозирования, теории игр усиливает роль наметившей­ся в последнее время тенденции применения средств вычисли­тельной техники в процессе строительства скважин [II, 17, 37, 76, 143].

Особенно велика роль статистических методов в решении за­дач во 2-м контуре управления.

Статистические оценки параметров процесса бурения, полу­ченные соответствующей обработкой результатов измерений по пробуренным ранее скважинам, используются при техническом проектировании строительства разведочных и эксплуатационных скважин, составлении гтн на бурение последующих скважин, выборе рационального сочетания «долото—турбобур» и для ре­шения других задач планирования и управления.

Таким образом, на количественном уровне процесс бурения может быть описан упорядоченным множеством детерминиро­ванных и вероятностных моделей:

V — <[/, /?!, /?2, …,

где…, Ят — отношения, определенные на множестве II.

В общем случае ход буровых работ описывается во времени некоторой траекторией в фазовом пространстве процесса буре­ния, координаты которого являются элементами множества (1.1). Однако оперирование с пространством высокой размерности, на координаты которого наложены ограничения в виде отношений /?,, /?2, •••, /?„„ а сами координаты £/, е ^/являются предикативны­ми функциями от элементов множества и, затрудняет построение общей модели на языке количественных отношений.

С целью упрощения модели необходимо произвести ее де­композицию, учитывая структурные и логические свойства и осо­бенности процесса бурения. Введем конечное множество струк­турных базовых элементов

5= {5], 52, …, …, 5^},

представляющее собой множество элементарных структурных еди­ниц процесса бурения, с которыми приходится оперировать в процессе проведения буровых работ. Например: долото, турбо­бур, лебедка, ствол скважины и т. п. Структурные свойства про­цесса бурения на уровне связей между отдельными элементами

е 5 могут быть представлены в виде булевой матрицы: [£• 5] х ||£/е)|| £. Каждой матрице такого вида будет соответство­вать своя структура элементов буровой и в свою очередь каждой структуре можно сопоставить характеристический вектор и от­ношения между его компонентами. Это позволит значительно снизить размерность фазового пространства системы, разбив его на множество частных фазовых пространств, соответствующих одной либо группам структур.

Для описания динамики системы при переходе от одной структуры к другой необходимо каждому переходу поставить в соответствие некоторый предикат, тоже заданный на мно­жестве и.

Однако подобная модель не будет полной, так как по ней нельзя осуществлять прогноз и проверять различные гипотезы. Поэтому необходимо ввести множество технологических опера­торов, под которыми будем понимать элементарные управляю­щие воздействия на объект.

Каждый оператор переводит буровую скважину из одного со­стояния в другое.

Пусть

В = {В, Вг, В:, …, В,,},

где В — конечное множество буримых скважин В/. Каждой буровой Д е В соответствует некоторое множество производимых на ней технологических операций

Д = {^1> В2, …, Д, …, Д,,},

где Д — у’-я технологическая операция;

т — общее число технологических операций.

За полное время бурения /-й скважины Т1 образуется неко­торая стохастическая последовательность технологических операций:

(1.18)

(Д)ь (ДЬі •••> (Д)/> •••! (В,)к,

где /= 1, 2, /с — порядковый номер технологической

операции.

Каждой операции (^^соответствует элемент є Т,, пред­ставляющий собой затраты времени на данную операцию. Полное время бурения 1-й скважины Т• представляется как сумма затрат времени на все технологические операции и простои:

Т-, — X tf — Ты + Ты,

/=1

где Тъ, — затраты времени на механическое бурение;

Та, — затраты времени на все остальные операции и простои.

Каждая конкретная операция, принадлежащая конечному мно­жеству состояния буровой (1.18), характеризуется наличием ряда признаков. Под признаками будем понимать либо технологиче­ские параметры, либо их производные, либо определенные ло­гические условия. При задании информационных признаков необходимо пользоваться элементами теории алгебры высказы­ваний — логикой предикатов [9, 118].

Тогда можно заменить любой набор информативных призна­ков высказывательной функцией (предикатом), которая в общем случае имеет вид

Р (*,, …, х„). (1.19)

Подставляя вместо предметных переменных конкретные тех­нологические параметры, их производные или логические усло­вия, получим конечное множество предикатов

Р = {/>,, Ръ Р, п).

Из этого следует, что каждой /-й операции множества (1.18) должна соответствовать своя высказывательная функ­ция Р, е Р.

Обозначив истину символом «1», а ложь — «О», можно запи­сать матрицу Мр, строки которой соответствуют операциям FjF, а столбцы — Р, еР (см. табл. 1.1).

Таблица 1.1 Формализация процесса бурения / р, л р„, 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 рт 0 0 0 1

Элементы матрицы формируются исходя из условия:

П, если Р: = 1 для "[О, если Р/ = 0 для Р,-‘

Таким образом, описание буровой скважины на уровне коли­чественных, логических и структурных свойств и отношений наиболее полно определяет модель буровой скважины как объ­екта управления, так как позволяет формализовать одну из ос­новных функций ИИС — функцию автоматического распозна­вания и определения продолжительности операций, проводимых на буровой.

Комментарии запрещены.