 МОДЕЛИ ПРЕОБРАЗОВАНИЯ ЭНЕРГИИ ВОЗОБНОВЛЯЕМЫХ ИСТОЧНИКОВ
МОДЕЛИ ПРЕОБРАЗОВАНИЯ ЭНЕРГИИ ВОЗОБНОВЛЯЕМЫХ ИСТОЧНИКОВ
3.2.1. Преобразование водной энергии
В гидроэнергетике вопросам изучения характеристик речного стока посвещены работы Г. А. Гриневича, С. Н. Крицкого, Н. А. Картвелишвили, М. ФМенкеля, А. Г. Ивахненко, А. Ш. Резниковского, Г. Г. Сванидзе и др. Наибольшее распространение при описании речного стока получили модели стационарного случайного процесса, протекающего во времени приблизительно однородно и имеющего вид случайных колебаний вокруг некоего среднего значения, причем ни средняя амплитуда, ни характер этих колебаний не имеют существенных изменений с течением времени.
Стационарный случайный процесс обладает свойством эргодичности. Применимость свойств стационарности и эргодичности к стоковым рядам в гидрологии часто показывают с помощью кривых обеспеченности речного стока или расхода за большой период наблюдений. Модели описания гидрологических характеристик, представляемых как стационарный случайный процесс обобщены в работах А. Ш. Резниковского. Развитию такого подхода способствует ряд объективных причин: 1 — возможность использования мощного математического аппарата теории вероятностей, позволяющего получать достаточно достоверные решения; 2 — недостаточная
изученность процесса речного стока во времени и адекватного отражения его изменчивости с помощью математического анализа; 3— ограниченность данных наблюдений за речным стоком на большинстве рек, не позволяющих получить достоверный статистический материал.
Описание речного стока состоит из установления одномерных или многомерных законов распределения вероятностей его гидрологических характеристик и статистической оценки параметров этих распределений. Наиболее часто принимается гипотеза об одномерности функции распределения вероятностей стационарного случайного процесса, состояния которого независимы от времени.
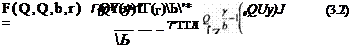 |
При этих допущениях в практике гидрологических расчетов наибольшее распространение получили функции распределения в виде так называемого трехпараметрического гамма-распред еления, которое также называется распределением Крицкого-Менкеля. Это распределение достаточно гибко и удовлетворительно описывает многие практически необходимые характеристики стока. Функция этого распределения применительно к расходу имеет вид:
где Q — расход; Q — математическое ожидание расхода; у и b — параметры, определяемые через коэффициент вариации и коэффициент асимметрии; Z— переменная интегрирования; Г(^ — гамма-функция.
В результате фундаментальных исследований советских ученых-гидрологов и гидроэнергетиков другие функции распределения (двухпараметрическое гамма-распределснис — распределение Пирсона третьего типа, распределение Джонсона, нормальное и логарифмическое распределения, предложенные иностранными учеными, стали не столь распространены, так как имеют менее универсальный характер, чем выражение (3.1).
Статистическая оценка параметров распределения базируется на анализе данных гидрологических наблюдений, которые ограничиваются несколькими десятками лет. По этой случайной выборке и происходит оценка функции распределения, которая также является случайной величиной. Поэтому цель статистического моделирования — дополнить имеющийся ряд наблюдений множеством других вариантов чередования многоводных и маловодных лет при принятых допущениях выявить параметры распределения: математическое ожидание, коэффициенты вариации и асимметрии, коэффициенты корреляции (для многомерных распределений) и другие характеристики.
Хорошо проработанный математический аппарат предлагаемых методов моделирования речного стока, дает достоверные результаты при наличии сравнительно длинных (измеряемых десятками лет) рядов наблюдений, однако он крайне громоздкий для практического использования при создании энергетических комплексов на малых реках, имеющих весьма ограниченные периоды наблюдений за стоком. В этих случаях можно пренебречь многомерностью распределения и использовать более простые модели, основанных на методах Монте-Карло и таблиц Фостера или Крицкого-Менкеля.